强化学习（五）—— AlphaGo与Alpha Zero

1. AlphaGo

1.1 论文链接

查看原文

1.2 输入编码（State）

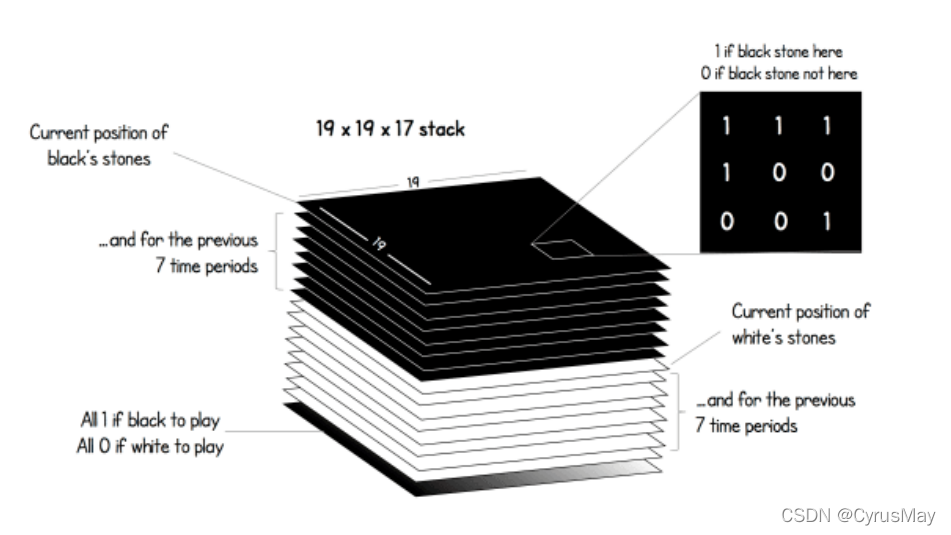
• 棋盘大小：[19,19]的矩阵, 落子则为1，反之为0。
• Input Shape:[19,19,17]。
• 白棋当前状态及其过去7步的状态：[19,19,1]与[19,19,7]。
• 黑棋当前状态及其过去7步的状态：[19,19,1]与[19,19,7]。
• 当前到谁落子：[19,19,1] (黑棋全为1，白棋全为0)

1.3 训练及评估流程

1. 使用behavior cloning 对策略网络进行初步训练；
2. 两个策略网络互相对弈，并使用策略梯度对策略网络进行更新；
3. 使用策略网络去训练状态价值网络；
4. 基于策略网络和价值网络，使用蒙特卡洛树（Monte Carlo Tree Search， MCTS）进行搜索。

1.4 模仿学习（Behavior Cloning）

通过Behavior Cloning从人的经验中初始化策略网络的参数，策略网络的结构为：
随机初始化网络参数后，基于人类对弈的落子序列数据，进行模仿学习（分类任务），使用交叉熵作为损失函数进行参数更新：

1. 观测得到状态：$$s_t$$
2. 使用策略网络进行预测$$p_t=[\pi (1|s_t;\theta ),\pi (2|s_t;\theta ),...,\pi (361|s_t;\theta )]$$
3. 高级人类玩家采取的动作为$$a_t^{\ast }$$
4. 策略网络的预测进行one-hot编码后，和人类玩家的动作进行交叉熵计算，并更新网络参数。
   模仿学习可认为是循规蹈矩。

1.5 策略网络依据策略梯度进行学习

1. 两个策略网络进行对弈直到游戏结束。Player V.S. Opponent，Player 使用策略网络最新的参数，Opponent随机选用过去迭代中的网络参数。
2. 得到对弈的序列数据：$$s_1,a_1,s_2,a_2,s_3,a_3,...,s_T,a_T$$
3. Player获得的回报为：$$u_1=u_2=u_3=u_T(赢了为1，输了为-1)$$
4. 近似策略梯度(连加)$$g_{\theta }=\sum _{t=1}^T\frac{\partial log(\pi (\cdot |s_t;\theta ))}{\partial \theta }\cdot u_t$$
5. 参数更新$$\theta \leftarrow \theta +\beta \cdot g_{\theta }$$

1.6 价值网络训练

• 状态价值函数：$$V_{\pi }(S)=E(U_t$$