通过仿真理解超外差混频过程

通过一个简要的仿真说明最基本的超外差变频链路构成。

文章目录

• 前言
• 一、混频器
• 二、中频滤波
• 二、镜像频率
• 总结

---

前言

通过一个简要的仿真说明最基本的超外差变频链路构成。

---

一、混频器

模拟射频域的混频可以用两个余弦函数在时域的乘法描述，假定射频为160MHz，本振200MHz，通过三角函数的积化和差公式，可以得到混频输出，为差频40MHz与和频360MHz的和信号，所得到的频谱如图1所示。

注意混频器的射频、本振及混频输出均为实数信号，实数信号的正负频谱对称，因此这里只关注正频谱部分。此外，虽然讨论的是射频模拟域的连续信号，但为了仿真方便，仿真设置采样速率为1GHz，则对应图1正频率范围为0~500MHz。这个混频的过程对应到数字硬件实现就是一个DSP乘法器完成两个DDS产生单音信号时域相乘的过程，相关搜索可以找到教程。

图1 超外差混频频谱

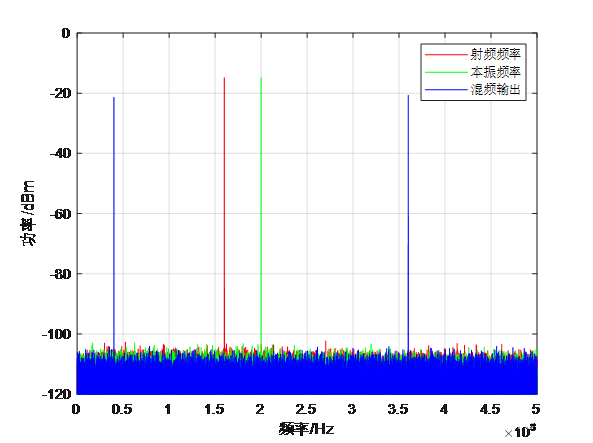
二、中频滤波

图1混频得到了两个频率，实际需要射频与中频一一对应，因此需要在混频后添加滤波器滤除不需要的那个，假定只需要保留40MHz的差频项，通过构建一个图2所示低频选通高频抑制的滤波器，滤除不需要的360MHz，剩下的即为所需的中频信号。程序中采用如下代码段产生低通滤波器。

%  构造低通滤波器
Order = 32;       % 滤波器阶数
Fpass = fs/8;     %  通带频率
Fstop = Fpass*2 % 阻带频率
Wpass = 0.1;      % 通带权重
Wstop = 40;       % 阻带权重
dens = 20; 
b = firpm(Order, [0 Fpass Fstop fs/2]/(fs/2), [1 1 0 0], [Wpass Wstop], {dens});
Hd = dfilt.dffir(b);
fvtool(Hd);          % 查看滤波器

图2 低通滤波器曲线

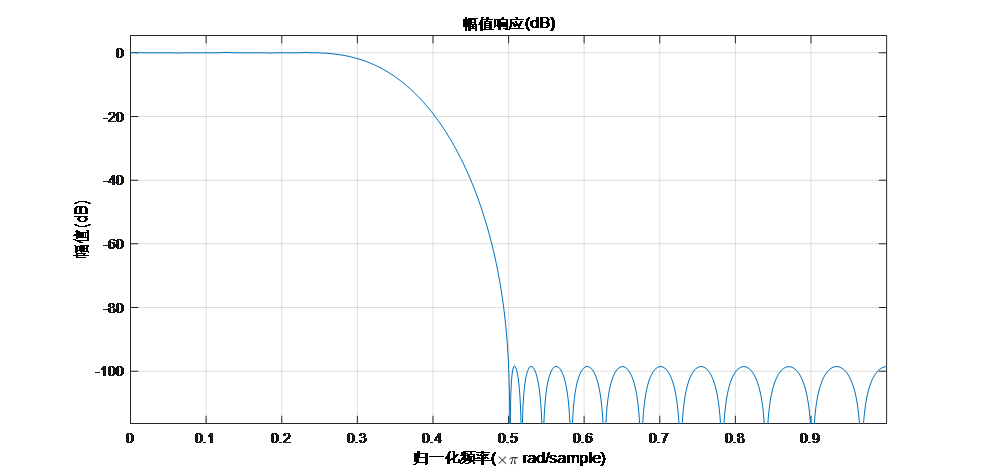
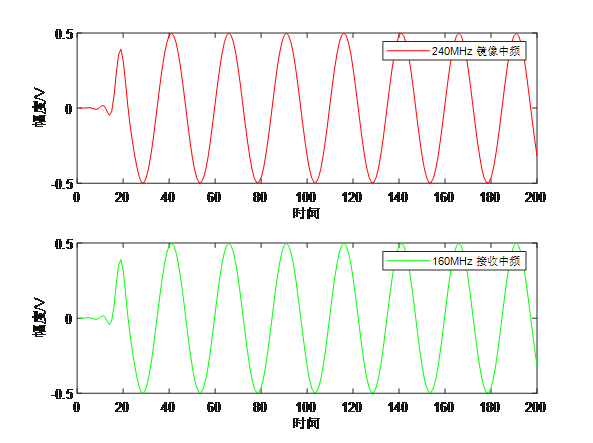
图3为中频滤波后频谱，图4给出了滤波前后时域波形（前200个时间快拍）的对比，滤波后输出为一个干净的单音信号。

图3 混频输出滤波后频谱

图4 滤波前后时域波形

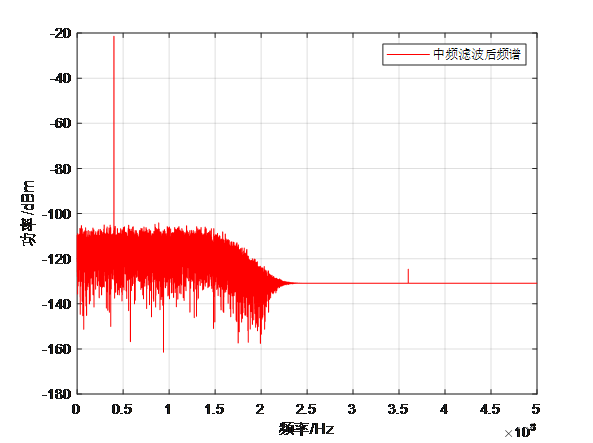
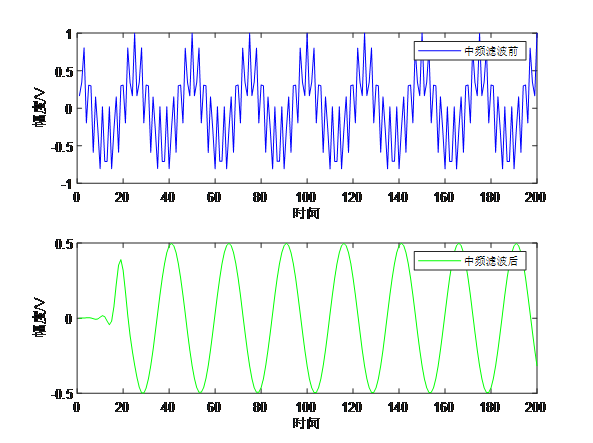
从图2的混频结果得到图4的混频结果，需要在混频器后再加一个低通滤波器。

三、镜像频率

之所以称为超外差，是由于镜像频率的存在。接收频率与镜像频率相对与混频本振是镜像关系，比如这里讨论的本振200MHz，200MHz±40MHz（中频频率）这两个频率互为镜像频率。进一步仿真，保持本振频率不变为200MHz，当射频改为240MHz时，依然采用三角函数积化和差，得到混频输出为差频40MHz与和频480MHz。过程如图5所示。

图5 镜像频率超外差混频频谱图

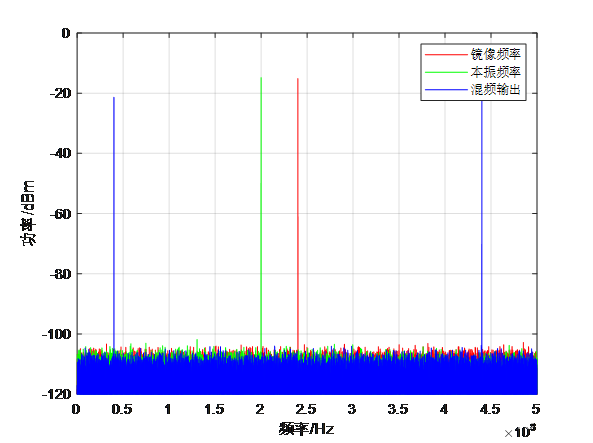
可以预计，通过低通把480MHz滤除后，得到的40MHz信号与图4相同。也就是说，本振为200MHz的这个变频过程将无法区分160MHz频率与240MHz频率。

图6 镜像频率混频输出与图4输出对比

因此为了区分这两个频率，需要在混频前加滤波器保留160MHz，而把可能存在的240MHz滤除。

至此，得到了常规超外差的最简单结构，镜像抑制滤波器+混频器+中频滤波器，这个过程能够使输入频率与输出频率一一对应。

---

总结

为了实现射频频率与中频频率的映射和频率搬移，一步步仿真得到了最简化的超外差变频结构。