力扣剑指Offer 第20天分治算法（中等）剑指 Offer 07. 重建二叉树剑指 Offer 16. 数值的整数次方剑指 Offer 33. 二叉搜索树的后序遍历序列

最新推荐文章于 2026-01-04 19:40:08 发布

原创最新推荐文章于 2026-01-04 19:40:08 发布 · 339 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode #分治算法

leetcode 专栏收录该内容

28 篇文章

订阅专栏

本文深入探讨了利用分治算法解决二叉树重建、数值整数次方计算以及二叉搜索树后序遍历序列验证的问题。针对每个问题，文章提供了详细的解题思路和递归、非递归的解决方案，揭示了二叉树特性和分治策略在算法设计中的关键作用。

力扣剑指Offer 第20天分治算法（中等）剑指 Offer 07. 重建二叉树剑指 Offer 16. 数值的整数次方剑指 Offer 33. 二叉搜索树的后序遍历序列

剑指 Offer 07. 重建二叉树

题目

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

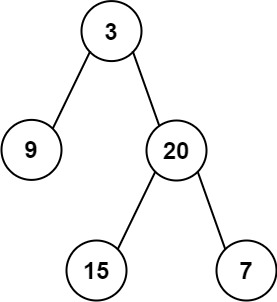
在这里插入图片描述

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

限制：

0 <= 节点个数 <= 5000

题解

分治二叉树遍历的性质

前序遍历列表：第一个元素永远是【根节点 (root)】

中序遍历列表：根节点 (root)【左边】的所有元素都在根节点的【左分支】，【右边】的所有元素都在根节点的【右分支】

算法思路：

通过【前序遍历列表】确定【根节点】

将【中序遍历列表】的节点分割成【左分支节点】和【右分支节点】

递归寻找【左分支节点】中的【根节点】和【右分支节点】中的【根节点】

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    private int[] preorder=null;
    private HashMap<Integer,Integer>map=null;
    private int pre=-1;
    private TreeNode divide(int l,int r){
        if(++pre>=preorder.length)return null;
        int in=map.get(preorder[pre]);
        TreeNode node=new TreeNode(preorder[pre]);
        // System.out.println(node.val+" in:"+in);
        if(l<in)node.left=dfs(l,in-1);
        if(r>in)node.right=dfs(in+1,r);
        return node;
    }
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(preorder.length==0)return null;
        this.preorder=preorder;
        map=new HashMap<>();
        for(int i=0;i<inorder.length;i++){
            map.put(inorder[i],i);
        }
        return divide(0,inorder.length-1);
    }
}

剑指 Offer 16. 数值的整数次方

题目

实现pow(x, n) ，即计算 x 的 n 次幂函数（即，xⁿ）。不得使用库函数，同时不需要考虑大数问题。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：pow(2,-2) = pow(0.5,2) = 0.25

提示：

-100.0 < x < 100.0
-2³¹ <= n <= 2³¹-1
-10⁴ <= xⁿ <= 10⁴

题解

快速幂

边界：幂为0返回1

幂为奇数则将幂-1，结果乘以一个底数

幂为偶数则将幂除以2，底数平方

（相当于将原本的求复杂幂转换为求平方，将底数与幂做微妙的转换，使得幂一步步开平方急速降维）

本题虽然数据在int范围内，但是由于我们对幂的取反操作，使得当幂等于Integer.minValue时取反溢出发生错误！所以得开long！

递归实现

class Solution {
    private double pow(double x,long n){
        if(n==0L)return 1.0;
        if((n&1L)==1L)return pow(x,n-1L)*x;
        return pow(x*x,n/2L);
    }
    public double myPow(double x, int n) {
        if(n==0)return 1;
        if(x==0.0)return 0;
        long m=n;
        if(m<0){
            x=1.0/x;
            m=-m;
        }
        return pow(x,m);
    }
}

非递归实现

class Solution {
    public double myPow(double x, int n) {
        if(n==0)return 1;
        if(x==0.0)return 0;
        long m=n;
        if(m<0){
            x=1.0/x;
            m=-m;
        }
        double ans=1;
        while(true){
            if(m==0)break;
            if((m&1)==1){
                ans*=x;
                m--;
            }else{
                x*=x;
                m/=2L;
            }
        }
        return ans;
    }
}

剑指 Offer 33. 二叉搜索树的后序遍历序列

题目

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

参考以下这颗二叉搜索树：

示例 1：

输入: [1,6,3,2,5]
输出: false

示例 2：

输入: [1,3,2,6,5]
输出: true

提示：

数组长度 <= 1000

题解

分治

二叉搜索树的性质：左子树的值小于根值，右子树的值大于根的值
后序遍历：先递归搜索左子树，再递归搜索右子树，然后输出当前节点
无重复值节点

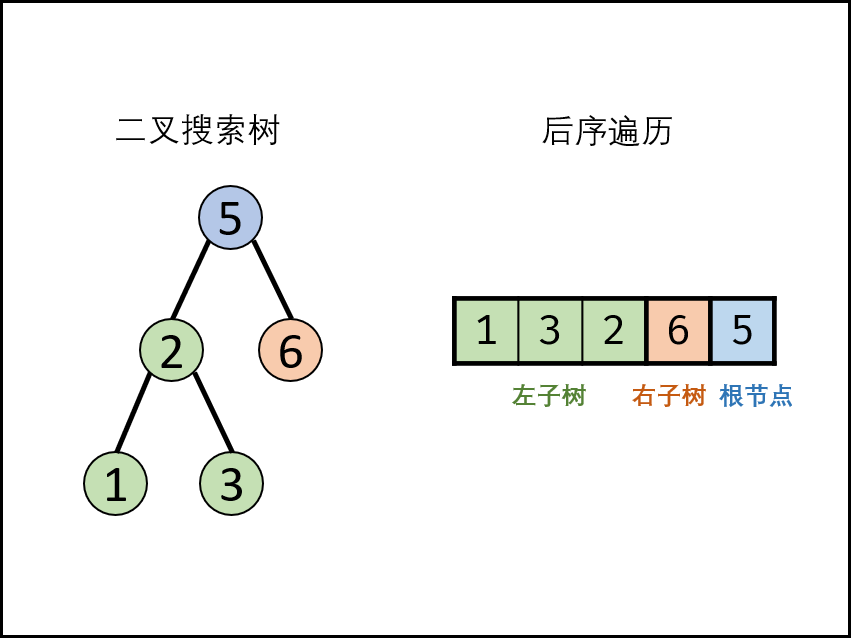
在这里插入图片描述

从最右的节点（根节点）开始，将左边数组划分为左子树（小于根值）与右子树（大于根值）

（如果在划分时发现不符合条件则说明不是二叉搜索树返回false）

边界：划分后的数组长度小于等于3时（任意3个元素都可以组成一个二叉搜索子树）

class Solution {
    private boolean divide(int[] postorder,int l,int r){
        // System.out.println("l:"+l+" r:"+r);
        if(r-l<=2)return true;
        int i=l,root=postorder[r];
        while(i<r&&postorder[i]<root)i++;//寻找右区域的左端
        int j=i;
        while(j<r&&postorder[j]>root)j++;//检测右区域是否符合条件（全部大于根）
        // System.out.println("i:"+i+" j:"+j);
        if(j!=r)return false;
        return divide(postorder,l,i-1)&&divide(postorder,i,r-1);
    }
    public boolean verifyPostorder(int[] postorder) {
        if(postorder.length<=2)return true;
        return divide(postorder,0,postorder.length-1);
    }
}