蓝桥杯2015初赛生命之树 DFS图解

大家觉得写还可以，可以点赞、收藏、关注一下吧！
也可以到我的个人博客参观一下，估计近几年都会一直更新！和我做个朋友吧！https://motongxue.cn

---

蓝桥杯2015初赛生命之树😁

题目描述

在X森林里，上帝创建了生命之树。
他给每棵树的每个节点(叶子也称为一个节点)上，都标了一个整数，代表这个点的和谐值。
上帝要在这棵树内选出一个非空节点集S，使得对于S中的任意两个点a,b，都存在一个点列 {a, v1, v2, …, vk, b}
使得这个点列中的每个点都是S里面的元素，且序列中相邻两个点间有一条边相连。
在这个前提下，上帝要使得S中的点所对应的整数的和尽量大。
这个最大的和就是上帝给生命之树的评分。
经过atm的努力，他已经知道了上帝给每棵树上每个节点上的整数。
但是由于 atm 不擅长计算，他不知道怎样有效的求评分。
他需要你为他写一个程序来计算一棵树的分数。

输入

第一行一个整数 n 表示这棵树有 n 个节点。(0<n<=10^5)
第二行 n 个整数，依次表示每个节点的评分。(每个节点的评分不超过10^6)
接下来 n-1 行，每行 2 个整数 u, v，表示存在一条 u 到 v 的边。
由于这是一棵树，所以是不存在环的。

输出

输出一行一个数，表示上帝给这棵树的分数。

样例输入

5
1 -2 -3 4 5
4 2
3 1
1 2
2 5

样例输出

8

分析

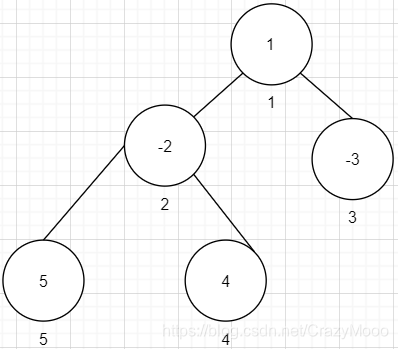
由题目画图可得：

分析

1. 由于有n个结点，n-1条边，所以这个图最终是能构成一棵树
2. 我们可以把图中的一个结点拎起来，当成这个图所构成树的根
3. 现在可以把题目转换成求树中最大的子树权值和了
4. 如图所示，5+4+(-2)+1=8为输入数据的答案
   

步骤

1. 输入数据，并将一条边的两个端点存入邻接表中
2. 递归的寻找跟当前结点有边的点，然后，将孩子结点的权值和**（大于0才加）加到w[root]当前结点的权值和，每次更新ans，然后我们就能得知当树的根节点为1时，他的子树中权值和最大为ans，即为题目所求解**

注意

在Java中使用邻接表的方法，Java中用 ArrayList<Integer>[] g = new ArrayList[n + 1]，cpp中用 vector<int> a[100]，超实用哦👌

在图的节点数非常多的情况下，用了邻接表可以有效防止开辟空间过大，造成内存超限MemorylimitExceeded
此外，这份一模一样的代码，用Java居然过不了
http://oj.ecustacm.cn/problem.php?id=1262，然而cpp却可以，并且，据说Java版本由于语言特性，提交到蓝桥杯官网也只能得到50%的分数，而cpp却能满分。奇奇怪怪🤧

代码

/*
 * @Author: motongxue
 * @Date: 2020-10-14 16:35:43
 * @LastEditors: motongxue
 * @LastEditTime: 2020-10-14 18:33:57
 * @Blog: https://motongxue.cn
 * @Description: 2015年Java B组 第10题 生命之树
 * 无根树转有根树的递归
 */

import java.util.ArrayList;
import java.util.Scanner;

public class Main {
    static int n;
    static Long ans = 0L;
    static Long[] w;
    static ArrayList<Integer>[] g;  
    // Java中用 ArrayList<Integer>[] g = new ArrayList[n + 1] 
    // cpp中用  vector<int> a[100]

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        w = new Long[n + 1];
        int x, y;
        g = new ArrayList[n + 1];
        for (int i = 0; i < n; i++) {
            w[i + 1] = sc.nextLong();    // 读入数据
            g[i+1] = new ArrayList<>();  // 初始化
        }
        for (int i = 1; i < n; i++) {
            x = sc.nextInt();
            y = sc.nextInt();
            g[x].add(y);                // 边的两个端点建立连接
            g[y].add(x);
        }
        dfs(1, -1);                     // 把1认为是树的根结点，无父结点
        System.out.println(ans);
    }
    /**
     * root 作为根所代表的子树有一个最大权和，将其储存在w[root]中
     * @param root  此时的结点
     * @param fa    root结点的父亲结点
     */
    private static void dfs(int root, int fa) {
        for (int i = 0; i < g[root].size(); i++) {  //遍历跟root相连通的点
            Integer child = g[root].get(i);
            if (child == fa)    // 如果判断孩子结点是否是父亲结点。防止进入死循环 1->2 2->1
                continue;
            dfs(child, root);   // 对子结点进行递归
            if (w[child] > 0)   // 如果子结点及其子树权值和大于零，则可以加入到父节点的权值
                w[root] += w[child];
        }
        ans = Math.max(ans, w[root]);   // 每次更新ans
    }
}

#include <iostream>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int n;
LL ans = 0L;
LL w[N];
vector<int> g[N];
// Java中用 ArrayList<Integer>[] g = new ArrayList[n + 1]
// cpp中用  vector<int> a[100]

/**
 * root 作为根所代表的子树有一个最大权和，将其储存在w[root]中
 * @param root  此时的结点
 * @param fa    root结点的父亲结点
 */
void dfs(int root, int fa)
{
    for (int i = 0; i < g[root].size(); i++)
    { //遍历跟root相连通的点
        int child = g[root][i];
        if (child == fa) // 如果判断孩子结点是否是父亲结点。防止进入死循环 1->2 2->1
            continue;
        dfs(child, root); // 对子结点进行递归
        if (w[child] > 0) // 如果子结点及其子树权值和大于零，则可以加入到父节点的权值
            w[root] += w[child];
    }
    ans = max(ans, w[root]); // 每次更新ans
}
int main()
{
    scanf("%d", &n);
    int x, y;
    for (int i = 0; i < n; i++)
        scanf("%lld", &w[i + 1]);

    for (int i = 1; i < n; i++)
    {
        scanf("%d %d", &x, &y);
        g[x].push_back(y); // 边的两个端点建立连接
        g[y].push_back(x);
    }
    dfs(1, -1); // 把1认为是树的根结点，无父结点
    printf("%lld\n", ans);
}

最后

其实这就是一个树形DP 的 题目了，是不是理解上也还行？没想到居然写着写着就能写到一道树形动态规划的题目。棒哦😂
树形DP在动态规划中也是一类题目了，今天先介绍到这里，有兴趣还麻烦关注我哦👏

---

2020年10月14日更

大家觉得写还可以，可以点赞、收藏、关注一下吧！
也可以到我的个人博客参观一下，估计近几年都会一直更新！和我做个朋友吧！https://motongxue.cn

---