【人工智能数学基础】——流形学习解密：从高维纠缠到低维本质的几何拓扑革命

最新推荐文章于 2025-12-23 21:54:00 发布

原创

最新推荐文章于 2025-12-23 21:54:00 发布 · 958 阅读

19 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #学习 #机器学习 #深度学习 #算法 #神经网络 #python

🌟 前言：流形学习——AI世界的"数据解结者"

🌌 结语：流形学习——在维度褶皱中寻找真理的坐标

📚 扩展阅读：

🔧 实战建议：

🌟 前言：流形学习——AI世界的"数据解结者"

考古学家解开古代卷轴的褶皱，流形学习解开高维数据的本征维度。这个源自微分几何的数学工具，以"局部平直，全局弯曲"的哲学重塑了数据降维的认知范式。本文将带您深入黎曼流形的数学核心，用代码重现数据本质维度的提取奇迹，揭示如何通过测地线距离在维度诅咒的迷雾中开辟通途。

一、流形学习的数学基石：微分几何与拓扑学

1.1 流形假设与维度诅咒

流形定义：

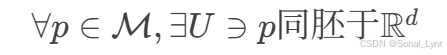
维度灾难：
$n \geq O\left(\left(\frac{1}{\epsilon}\right)^D\right) \quad \text{vs} \quad n \geq O\left(\left(\frac{1}{\epsilon}\right)^d\right)$

1.2 核心算法数学框架对比

算法	数学原理	优化目标	复杂度
Isomap	测地距离保持	$\min \\|D_G - D_Y\\|_F^2$	$\mathcal{O}(n^3)$
LLE	局部线性重构	$\min \sum \\|x_i - \sum W_{ij} x_j\\|^2$	$\mathcal{O}(n k^3)$
t-SNE	概率分布匹配	$\text{KL}(P \parallel Q)$	$\mathcal{O}(n^2)$
UMAP	模糊拓扑保持	$\text{Cross-Entropy}$	$\mathcal{O}(n^{1.14})$