二叉搜索树详解与操作-优快云博客

本文介绍了二叉搜索树的定义，特点以及相关算法，包括查找指定关键码、插入新值和判断是否为二叉搜索树的方法。通过中序遍历规则，详细解释了如何验证一棵二叉树是否符合二叉搜索树的特性。

文章目录

定义
相关算法

定义

二叉搜索树或者是一颗空树，或者是具有下列性质的二叉树：

每个节点都有一个作为搜索依据的关键码，所有节点的关键码互不相同。
左子树(如果存在)上所有的节点的关键码都小于根节点的关键码。
右子树(如果存在)上的所有节点的关键码都大于根节点的关键码
左子树和右子树也是二叉搜索树。

二叉搜索树的结构：

class BinarySearchTree{
    private BstNode root;
    private BstNode cur;

    class BstNode{
        private int key; // 关键码
        private BstNode leftChild; //左孩子
        private BstNode rightChild; //右孩子
        private BstNode parent; // 双亲

        public BstNode(){
            key = 0;
            leftChild = rightChild = parent = null;
        }

        public BstNode(int key){
            this.key = key;
            leftChild  = rightChild = parent = null;
        }

        public BstNode(int key,BstNode parent,BstNode leftChild,BstNode rightChild){
            this.key = key;
            this.leftChild = leftChild;
            this.rightChild = rightChild;
            this.parent = parent;
        }
    }

    public BinarySearchTree(){
        root = cur = null;
    }


    public BinarySearchTree(BstNode root){
        this.root = root;
    }
}

相关算法

在二叉搜索树中查找指定的关键码

实现思路：我们知道二叉搜索树的特点：每一棵二叉搜索树，其左孩子节点的关键码一定小于根节点的关键码，右孩子节点的关键码一定大于根节点的关键码。

① 所以我们首先要确定指定的关键码是存在左子树中还是右子树中。

② 确定好是在左子树还是右子树中，直接在确定的范围内搜索。

如果在左子树(或右子树)中搜索不到指定的关键码，则这个二叉树中一定不存在这个关键码。

代码实现：

 public boolean findVal(int kx){
        cur = root;
        boolean res = false;
        while(cur!=null && cur.key != kx){
            cur = cur.key > kx ? cur.leftChild : cur.rightChild;
        }

        // 跳出while循环说明 要么 ① cur == null ② 要么 cur.key ==kx
        if (cur!=null && cur.key == kx){
            res = true;
        }
        return res;
    }

向二叉搜索树中插入一个新的值

实现思路：

① 考虑空树的情况。

② 如果树不为空，考虑插入的范围。(插入左子树中，还是右子树中)

③ 确定好范围后，进行查找(查找指定的关键码是否已经存在与该二叉树中，如果存在，则不能进行插入，如果不存在，则可以插入)

④ 当确定好指定的关键码不存在于该二叉搜索树中，此时，new一个新的节点，但是我们不确定新new出来的节点的父节点是谁，所以我们需要有一个标记节点，始终指向cur的父节点。

代码实现：

public boolean insertValue(int kx){
        cur = root;
        BstNode tag = null;// 标记节点
        BstNode newNode = null;
        boolean res = true;
        if (cur == null){
            newNode = new BstNode(kx);
            cur = newNode;
            return res;
        }
        while(cur!=null && cur.key!=kx){
            tag = cur;
            cur = cur.key > kx ? cur.leftChild : cur.rightChild;
        }

        if (cur!=null && cur.key == kx){
            res = false;
        }else{
            newNode= new BstNode(kx);
            newNode.parent = tag;
            if (newNode.key < tag.key){
                tag.leftChild = newNode;
            }else{
                tag.rightChild = newNode;
            }
        }
        return res;
    }

判断一棵二叉树是否为二叉搜索树

还记得我们中序遍历规则吗？对于一棵子树来说，会先输出它的左孩子节点，再输出根节点，最后输出右孩子节点。

我们可以依据这个规则，来判断一棵二叉树是否为二叉搜索树。我们拎出一个二叉搜索树单独来看：
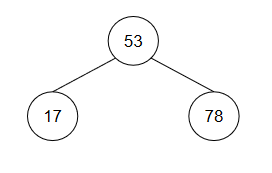
在这里插入图片描述
每次拿到的栈顶元素，都是某一棵二叉树搜索树的根节点，也是上一棵二叉搜索树的左孩子。于是，我们可以再引入一个标记节点，让这个节点指向栈顶元素。(例如：17这个节点，既是17这棵二叉搜索树的根节点，又是53这棵二叉搜索树的左孩子节点)

接着，我们就可以通过二叉搜索树的特性，来判断一棵二叉树是否为二叉搜索树。
代码实现：

 public boolean isBstTree(){
        BstNode pre = null;
        boolean res = true;
        if (cur==null) return res; //空树也可以认为是一颗二叉搜索树

        Stack<BstNode> stack = new Stack<>();
        while(cur!=null || !stack.empty()){
            while(cur!=null){
                stack.push(cur);
                cur = cur.leftChild;
            }
            cur = stack.pop();
            if (pre!=null && pre.key >= cur.key){
                res = false;
                break;
            }
            pre = cur;
            cur = cur.rightChild;
        }
        return res;
    }