区间DP入门（含模版）

1.模版引入

我们从洛谷一道题目开始讲解：石子合并（弱化版） - 洛谷

前缀和

首先，我们先要讲一个知识点叫做前缀和，其实前缀和和dp有一个很相似的特点，都是通过记忆前面的值推导出后面的值。

这个其实很简单，我就不详细解释了，a[i]就表示前i项和，它等于前i-1项加上第i项，这样做减少了时间复杂度，调用前i项和的时候很方便。

int main() {
    int n,i;
    std::vector<int>a(n);
    for (int p = 1; p <= n; i++) {
        std::cin >> i;
        a[i] = a[i - 1] + i;
    }
    return 0;
}

动态规划

石子合并问题（弱化版）

简单说一下题意：就是有n堆石块，每次可以合并相邻的两堆石块，总分+=这两堆石块的质量之和，让求最小总分。那么我们要把n堆石块合并成一堆石块，是不是可以让[1,1]这堆石块和[2,n]这堆石块合并([2,n]表示已经合并好的n-1堆石块），也可以让[1,2]和[3,n]合并，也可以[1,3]和[4,n]合并……，那么[2,n]又是由[2,3]和[4,n]合并而成，或者其他的方式，总之我们要从最小的开始合并，并且记录下每个区间合并而成的最小值。

所以我们要引入一个叫做状态转移方程的东西，这个东西就是区间dp的核心，找到它题目就写了一半了。在这个题里面，我们用dp[i][j]这个数组来记录在[i,j]这个区间的分数，那么假设现在有两个区间[i,k]和[k+1,j]，dp[i][j]可以由dp[i,k

然后我们要知道动态规划有哪几个步骤：1.初始化最小区间（最小区间的值必须是确定的吧，大区间都是由小区间推导而来的）2.枚举区间长度，枚举最左下标3.调用状态转移方程求大区间。

#define N 305
int a[N], weight[N];
int dp[N][N];
int main() {
    int n; std::cin >> n;
    for (int i = 1; i <= n; i++) {
        std::cin >> a[i];
        weight[i] += weight[i - 1] + a[i];
    }
    memset(dp, 1001, sizeof(dp));
    for(int i=1;i<=n;i++)dp[i][i]=0;


    
    return 0;
}

在这个题目中，区间长度为1的区间类似于dp[1][1],dp[2][2]这种，只有一个数，分数必然是0，其它的区间为什么初始化为1001，题目中石子的质量不超过1000，且这和状态转移方程有关。我们后面会用到这样一个式子dp[i][j] = std::min(dp[i][j], dp[i][k] + dp[k + 1][j] + weight[j] - weight[i - 1]);

看下面这张图

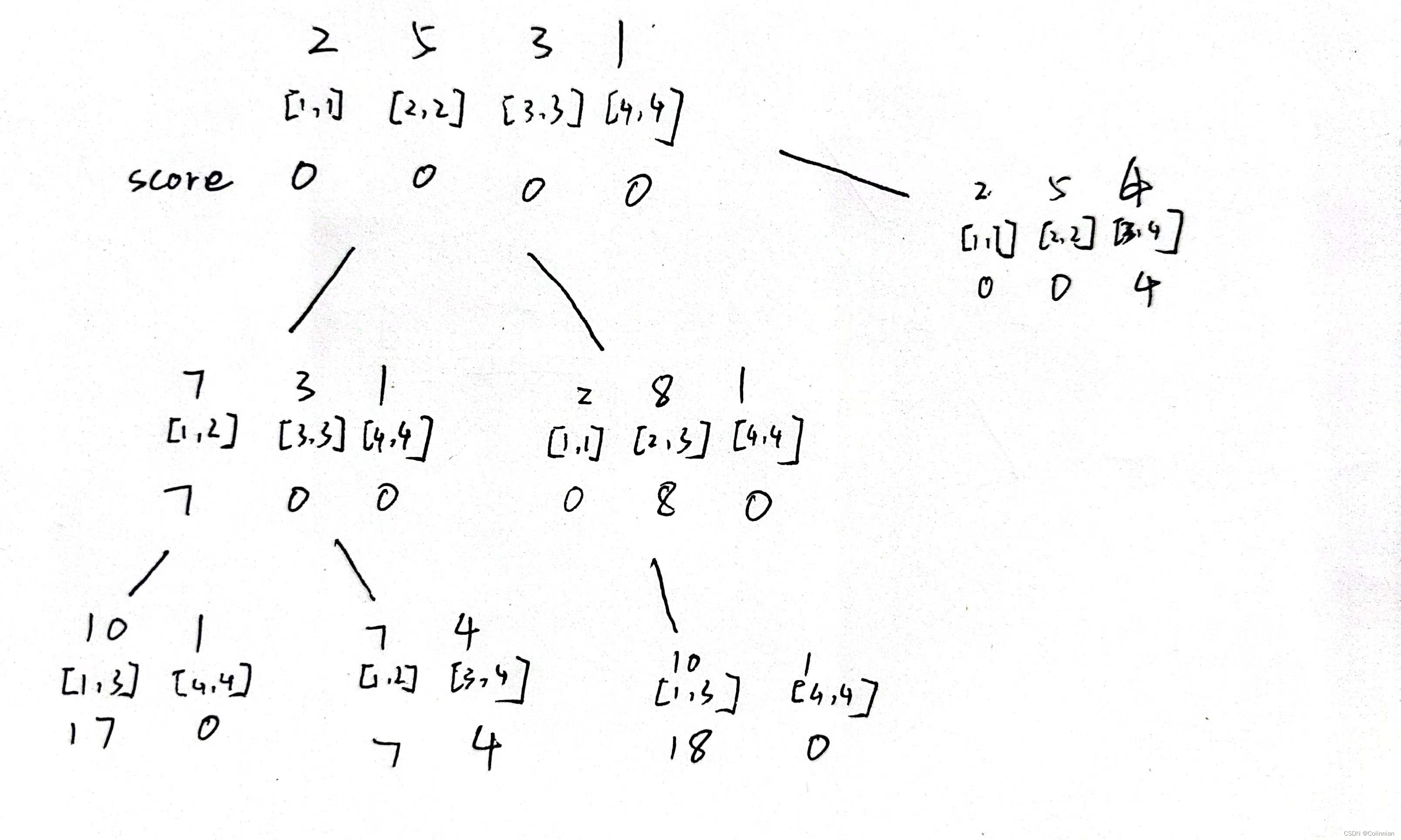
这张图并没有画全所有步骤，但是不难看出产生区间[1,3]的方式有很多种，所以我们要多次对比这次产生的dp[i][j]是都比上次大，试想一下如果dp[1][3]初始化为0或是一个小于17的数，在第一次产生区间[1,3]就是合成为10的那一堆，min函数会选择0而不是17。所以在这个地方我们要把除dp[i][i]的都初始化为大于1000.

接下来写枚举区间长度和枚举最左下标这一部分。这很简单。

#define N 305
int a[N], weight[N];
int dp[N][N];
int main() {
    int n; std::cin >> n;
    for (int i = 1; i <= n; i++) {
        std::cin >> a[i];
        weight[i] += weight[i - 1] + a[i];
    }
    memset(dp, 0x3f, sizeof(dp));
    for(int i=1;i<=n;i++)dp[i][i]=0;
    for (int len = 2; len <= n; len++) {
        for (int i = 1; i + len - 1 <= n; i++) {
             int j = i + len - 1;
            

            }
        }
    }
    std::cout << dp[1][n];
    return 0;
}

len=1的时候我们已经初始化过了，让len从2开始就好了，区间长度从1枚举到n就可以了，注意最左下标是由i决定的，假设i=2，n=4，len=4，那么产生的区间会变成[2,5],5显然已经超出了4，所以要让i+len-1<n.

接下来我们通过使用状态转移方程自动求出最后一个堆就好了。通过给定一个k，表示[i,k],[k+1,j]这两个区间产生的分数相加，并使用我们先前通过一维前缀和求出[i,j]的总重量weight[j]-weight[i-1]就得出来我们当前的分数。最后打印出来区间[1,n]的值就好了。

！！补充一下k为什么要小于j，因为定于j会越界，记得我们使用了dp[k+1][y]吗？

#define N 305
int a[N], weight[N];
int dp[N][N];
int main() {
    int n; std::cin >> n;
    for (int i = 1; i <= n; i++) {
        std::cin >> a[i];
        weight[i] += weight[i - 1] + a[i];
    }
    memset(dp, 0x3f, sizeof(dp));
    for(int i=1;i<=n;i++)dp[i][i]=0;
    for (int len = 1; len <= n; len++) {
        for (int i = 1; i + len - 1 <= n; i++) {
            int j = i + len - 1;
            for (int k = i; k < j; k++) {
                dp[i][j] = std::min(dp[i][j], dp[i][k] + dp[k + 1][j] + weight[j] - weight[i - 1]);
            }
        }
    }
    std::cout << dp[1][n];
    return 0;
}

模版

然后我们就可以引出区间dp的模版 

#define N 305
int a[N], weight[N];
int dp[N][N];
int main() {
    //输入与准备
   

    //初始化
    for (int len = 1; len <= n; len++) {
        for (int i = 1; i + len - 1 <= n; i++) {
            int j = i + len - 1;
            for (int k = i; k < j; k++) {
                //状态转移方程
            }
        }
    }
    std::cout << dp[1][n];
    return 0;
}

 当我做完这道题去做和它题目相同的一道NOI，正当我激动地把代码提交上去的时候……可想而知，全部WA。

当然我要讲的下面这到题也是有加强版的，别问我为什么不讲加强版题解，别问，看不懂，真的看不懂，我这种菜鸟只配套模版。

合并问题

题目在这[USACO16OPEN] 248 G - 洛谷

大致意思就是说可以合并相邻的数，合并后+1，这里合并的意思是2 2，合并后变成3.求最大值，一样的先初始化。

const int N = 250;
int f[N][N];
int main() {
    int n,ans=0; std::cin >> n;
    for (int i = 1; i <= n; i++) {
        std::cin >> f[i][i];
        ans = std::max(ans, f[i][i]);
    }
    
    return 0;
}

在这里我们用ans记录最大值，合并完成后整组数据不一定合并成一个，所以我们没法从中数组中找到最大值打印，只能当它出现的时候记录下来。同时要考虑一种特殊情况，当数组没有变动怎么办，那我们是不是要从原数据中找到一个最大值，所以在输入的时候就顺便把最大值记录下来。

然后套用区间dp模版

const int N = 250;
int f[N][N];
int main() {
    int n,ans=0; std::cin >> n;
    for (int i = 1; i <= n; i++) {
        std::cin >> f[i][i];
        ans = std::max(ans, f[i][i]);
    }
    for (int len = 2; len <= n; len++) {
        for (int i = 1; i + len - 1 <= n; i++) {
            int j = i + len - 1;
            for (int k = 1; k < j; k++) {
                



            }
        }
    }
    printf("%d\n", ans);
    return 0;
}

然后找状态转移方程 在[i,j]区间内插入一个k，那么[i,k]和[k+1,j]这两个区间显然是连续的，那么只要当dp[i,k]==dp[k+1,j]即可，但是在有些区间内它们是没有子区间能够合并上来的，不为0的区间都是能够合并成一个数的区间，如果两个0挨着了是不是会出错，因为原数据中是不会出现0的，题目都说了在1到40之间，所以我们还要加上一个条件dp[i,k]==dp[k+1,j]!=0.

它的状态转移方程也很容易知道了无非就是dp[i,k]+1嘛。接下来写程序

const int N = 250;
int f[N][N];
int main() {
    int n,ans=0; std::cin >> n;
    for (int i = 1; i <= n; i++) {
        std::cin >> f[i][i];
        ans = std::max(ans, f[i][i]);
    }
    for (int len = 2; len <= n; len++) {
        for (int i = 1; i + len - 1 <= n; i++) {
            int j = i + len - 1;
            for (int k = 1; k < j; k++) {
                if (f[i][k] == f[k + 1][j] && f[i][k]) {
                    f[i][j] = std::max(f[i][j], f[i][k] + 1);
                    ans = std::max(ans,f[i][j]);
                }
            }
        }
    }
    printf("%d\n", ans);
    return 0;
}

 f[i][k]为0就不会执行if，"ans = std::max(ans,f[i][j]);",这里的max也是很有必要的，找到最大的那一个[i][j]区间嘛。最后打印ans即可。

文章到这里就结束了，如果对你有帮助，点个赞在走吧。这两道题的加强版等我研究明白了再讲吧，什么时候有时间再写，写一篇博客说实话要花挺长时间的

感慨与吐槽和给新手的一点建议（虽然我也是新手，半入门吧）

一下是我的一点吐槽，不想看的可以退出了。

我也是今天才开始学dp，从刚学C语言到现在快三个多月了，打了好几场比赛，发现好多题都是要用到dp的，不学dp根本不行，然后一学就被大神的题解给背刺了，看不懂根本看不懂，人家的题解时间复杂度可以直接降到n，而我只能抱着我这个的模版瑟瑟发抖。看了这么多题解最有感触的一点就是题解注释少而且对新手极其不友好，一上来来两个变量根本不知道啥意思就给你搞蒙圈了，只能不停地东查西查，然后狂摁F11去调试看程序每一步是怎么运行的。其次挺羡慕那些初高中就早早接触算法，信息学竞赛的，起步晚差距是真的大。

对于新手，先把基础的语法学完再来学算法吧，然后多去看题解，不能太难也不能太简单，要挑你看的懂但又看不懂的，然后通过在纸上模拟逻辑，调试，问chatgpt，问别人等等方式把它搞懂，然后多写博客，这就是费曼学习法，给别人讲懂了，你自己也有很大提升，一定要站在新手的角度去考虑怎么讲解这个知识点，博客是最好的方式，现实中想要给别人讲题，除非你是公认的大神，不然不会有人来问你的，如果你水平太菜，只会有那种拿着一长串代码的真新手来问你，这样的代码你也不会看吧，如果水平中等，大家都是这个水平，谁都不愿意问谁。所以多写博客，多打比赛，其余的也没什么了，多做题。等我成真大神的再专门写一篇吧。