【力扣】验证二叉搜索树

 🔥 博客主页： 我要成为C++领域大神
🎥 系列专栏：【C++核心编程】 【计算机网络】 【Linux编程】 【操作系统】
❤️ 感谢大家点赞👍收藏⭐评论✍️

本博客致力于分享知识，欢迎大家共同学习和交流。

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

 

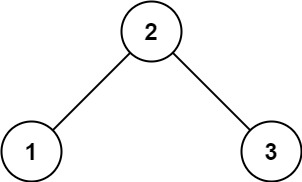
输入：root = [2,1,3]
输出：true

示例 2：

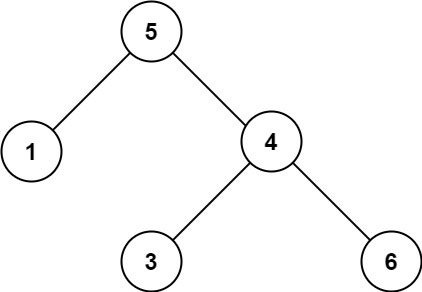
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

---

深度优先递归检查子树

思路

限定每个节点值的有效范围来判断二叉树是否是有效的BST

递归三部曲：

确定函数参数和返回值：参数是节点，左（右）子树值的范围。返回值当前子树是否是BST。
确定递归的终止条件：当前节点为空或者当前节点值不合法返回false
确定单层递归的逻辑：
检查左子树右子树是否合法

• 对于左子树，有效范围是 (left, node->val)；
• 对于右子树，有效范围是 (node->val, right)

代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        return dfs(root, numeric_limits<long>::min(),image.png
                   numeric_limits<long>::max());
    }
    bool dfs(TreeNode* node, long left, long right) {
        if (node == nullptr)
            return true;
        if (node->val <= left || node->val >= right)
            return false;
        return dfs(node->left, left, node->val) &&
               dfs(node->right, node->val, right);
    }
};