Python组蓝桥杯备赛超详细知识点总结笔记_排序算法篇

最新推荐文章于 2025-11-24 15:27:16 发布

原创最新推荐文章于 2025-11-24 15:27:16 发布 · 923 阅读

29 ·

CC 4.0 BY-SA版权

文章标签：

#排序算法 #算法 #蓝桥杯 #python #笔记

Python 组蓝桥杯备赛笔记专栏收录该内容

4 篇文章

订阅专栏

Python 组蓝桥杯备赛笔记（排序算法篇）

一、排序算法概述

排序算法是将一组数据按指定顺序（升序 / 降序）重新排列的基础算法，便于后续查找、统计等操作。根据时间复杂度、空间复杂度和稳定性的差异，可分为简单排序（O (n²)）、高效排序（O (nlogn)） 和特殊排序（基于分桶思想） 三类。二、冒泡排序（Bubble Sort）

算法名称	核心思想	时间复杂度（平均）	时间复杂度（最坏）	时间复杂度（最好）	空间复杂度	稳定性	适用场景	关键特点
冒泡排序	通过相邻元素比较交换，将大元素逐步 “冒泡” 到数组末尾	O(n²)	O(n²)	O (n)（优化后）	O(1)	稳定	小规模数据、教学演示、接近有序的数据	实现最简单，交换次数多，优化后可提前终止
选择排序	每轮从待排序部分选最小值，与待排序部分首位交换，逐步构建有序序列	O(n²)	O(n²)	O(n²)	O(1)	不稳定	小规模数据、硬件交换成本高的场景（如元素体积大）	交换次数少（最多 n-1 次），但比较次数固定，不稳定
插入排序	类比 “抓扑克牌”，将未排序元素插入到已排序部分的正确位置	O(n²)	O(n²)	O(n)	O(1)	稳定	小规模数据、接近有序的数据（如日志增量排序、Excel 局部排序）	局部调整效率高，对有序数据友好，稳定
希尔排序	按 “增量” 分组，对每组插入排序，逐步缩小增量至 1，最终完成排序	O(n^1.3)	O(n²)	O(n)	O(1)	不稳定	中等规模数据（n < 10000）、对空间敏感的场景	插入排序的升级，突破 O (n²) 复杂度，无需额外空间
快速排序	选基准值，将数组分为 “小于 / 等于 / 大于基准值” 三部分，递归排序子数组	O(n log n)	O (n²)（基准不当）	O(n log n)	O(log n)	不稳定	大规模数据（n ≥ 1000）、通用排序场景（数据库、文件排序）	平均效率最高，实现灵活，可通过优化基准值避免最坏情况
归并排序	递归拆分数组为两个子数组，分别排序后合并为有序数组（分治思想）	O(n log n)	O(n log n)	O(n log n)	O(n)	稳定	需稳定排序的大规模数据（电商订单排序）、外排序（数据存磁盘）	复杂度稳定，支持外排序，但空间开销大
堆排序	构建大顶堆，反复提取堆顶（最大值）并调整堆，直至所有元素有序	O(n log n)	O(n log n)	O(n log n)	O (1)（迭代）	不稳定	内存受限、需原地排序的大规模数据（如嵌入式系统）	利用堆的极值特性，空间效率高，但元素访问跳跃性大，缓存友好性差
计数排序	统计每个值的出现次数，通过前缀和计算位置，构建有序数组（非比较型）	O(n + k)	O(n + k)	O(n + k)	O(n + k)	稳定	小范围整数排序（如成绩 0-100、年龄 1-120）、作为基数排序子过程	线性时间排序，仅适用于整数，数据范围 k 需接近 n
基数排序	按数位（低位→高位或高位→低位）排序，每轮用计数排序作为子过程（非比较型）	O(d×(n + k))	O(d×(n + k))	O(d×(n + k))	O(n + k)	稳定	大整数排序（如身份证号）、字符串排序、数据范围大但数位少的场景	依赖数位拆分，可处理大范围数据，稳定性取决于子排序算法
桶排序	将数据分配到若干 “桶” 中，桶内单独排序（用其他算法），最后合并所有桶（分治型）	O (n)（理想）	O (n²)（极端分布）	O (n)（理想）	O(n + k)	稳定	数据均匀分布的场景（如用户年龄、商品价格区间固定）、分布式排序	效率依赖数据分布，均匀分布时接近线性时间，需合理设置桶数量

二、冒泡排序

冒泡排序是一种基础的交换排序算法，核心思想是通过相邻元素的比较与交换，将较大的元素逐步 “冒泡” 到数组末尾，较小元素自然向前移动。

def bubble_sort(a,n):	# n 为数组长度，a 为待排序数组
    # 外层循环：控制轮次，共 n-1 轮（i 从 1 到 n-1）
    for i in range(1, n):
        # 内层循环：控制比较范围，第 i 轮比较前 n-i 个元素（j 从 0 到 n-i-1）
        for j in range(n - i):
            # 相邻元素比较，前大后小则交换
            if a[j] > a[j + 1]:
                a[j], a[j + 1] = a[j + 1], a[j]

1. `visualgo`演示动画

请添加图片描述

2. 优化

基础冒泡排序在数组已有序时仍会执行 n-1 轮循环，可添加 “是否交换” 的标志位优化，减少无效轮次：

def bubble_sort(a,n):
    for i in range(1, n):
        swapped = False  # 标志位：记录本轮是否发生交换
        for j in range(n - i):
            if a[j] > a[j + 1]:
                a[j], a[j + 1] = a[j + 1], a[j]
                swapped = True  # 发生交换，置为 True
        if not swapped:  # 本轮无交换，说明数组已有序，提前退出
            break

优化效果：数组已有序时，仅需 1 轮循环（O(n)），大幅提升效率。

三、选择排序（Selection Sort）

选择排序是一种简单直观的排序算法，核心思想是每一轮从待排序元素中找出最小（或最大）的元素，将其与待排序部分的首位元素交换位置，从而逐步构建有序序列。

def selection_sort(a,n):
    # 外层循环：控制轮次（0 到 n-2，共 n-1 轮）
    for i in range(n - 1):
        # 初始化最小值为当前轮次起始元素
        min_value = a[i]
        min_idx = i
        # 内层循环：从 i 到 n-1 查找最小值
        for j in range(i, n):
            if a[j] < min_value:
                min_value = a[j]
                min_idx = j
        # 交换最小值与当前轮次起始元素
        a[i], a[min_idx] = a[min_idx], a[i]

`visualgo`演示动画

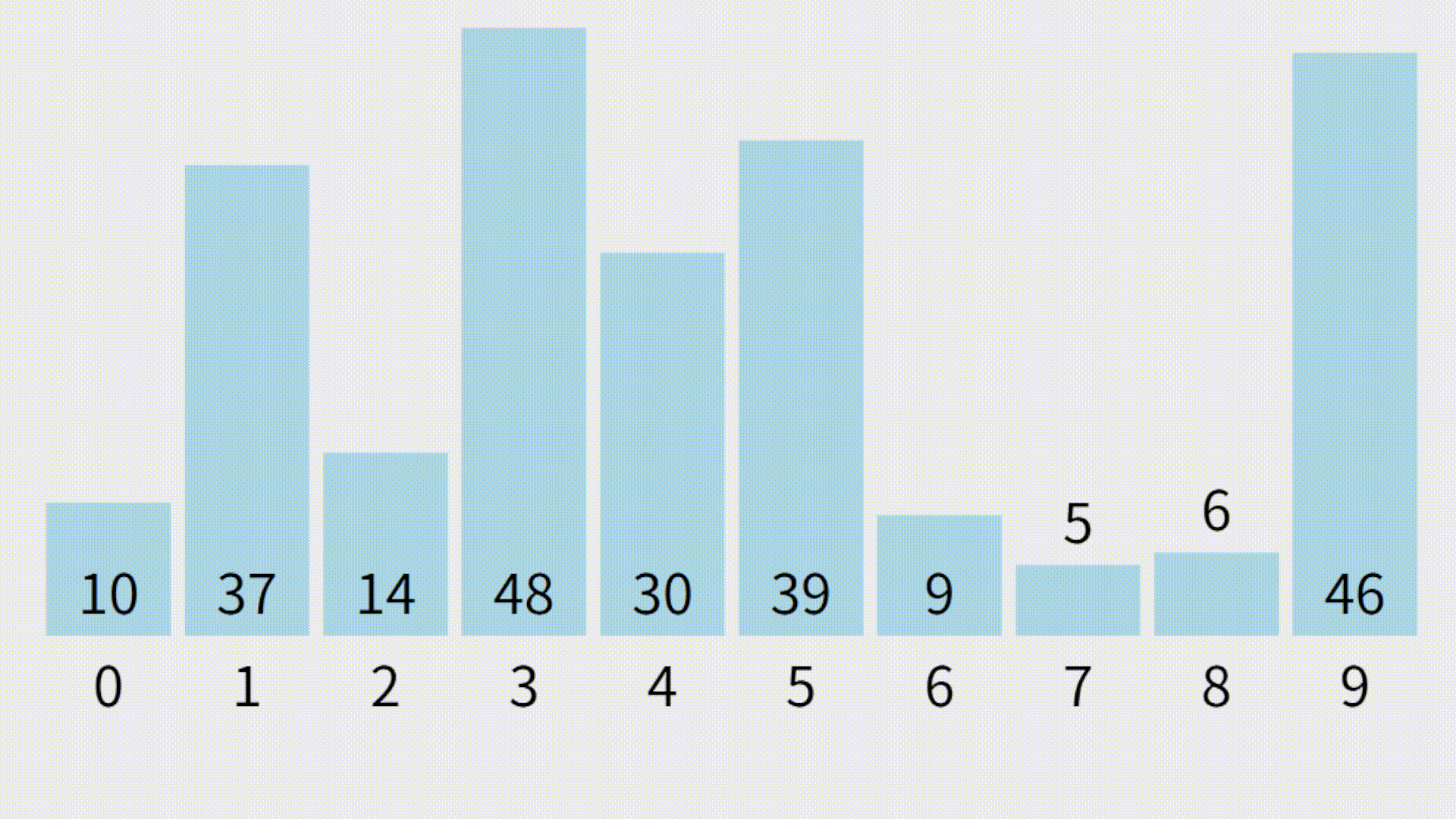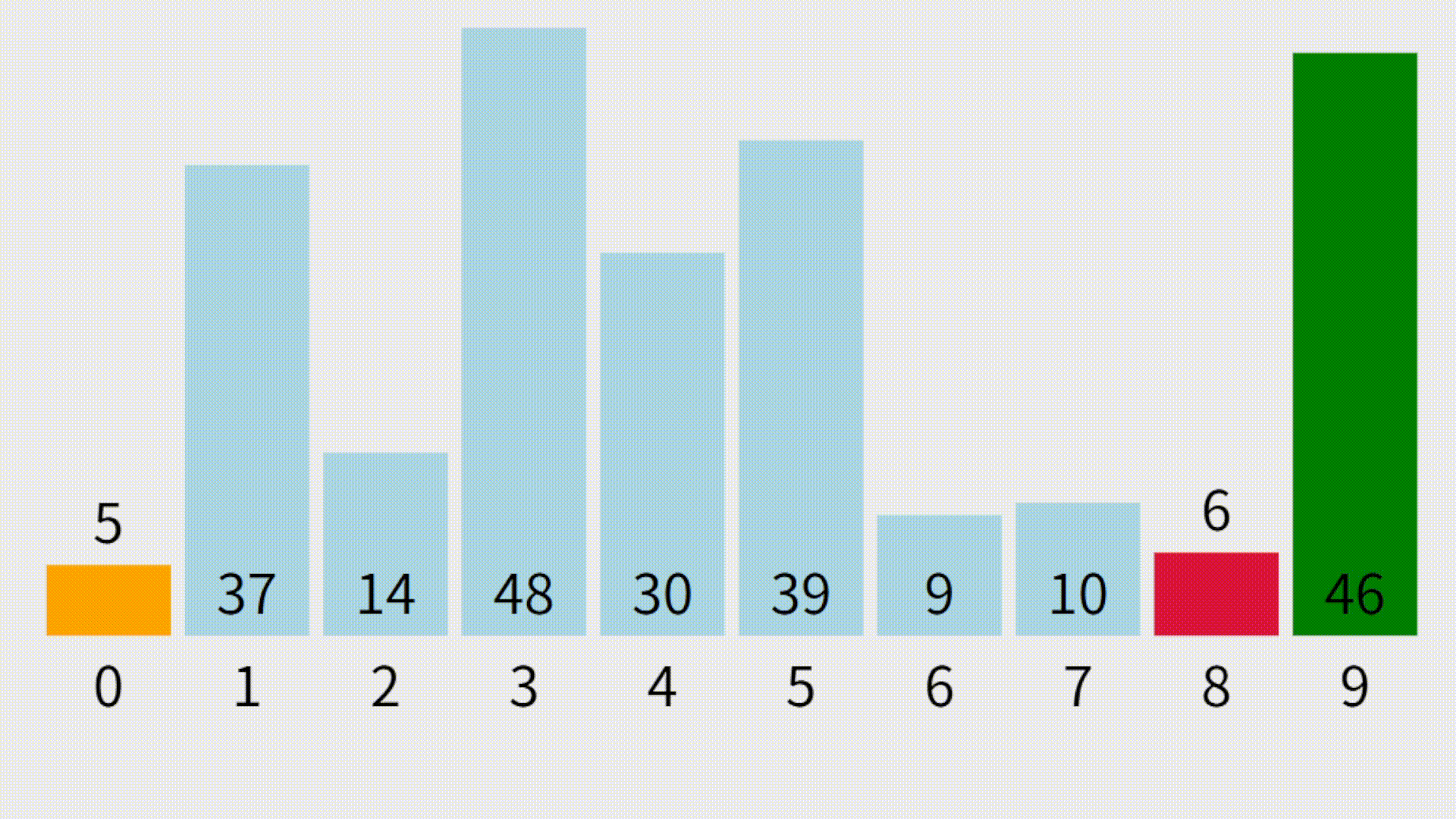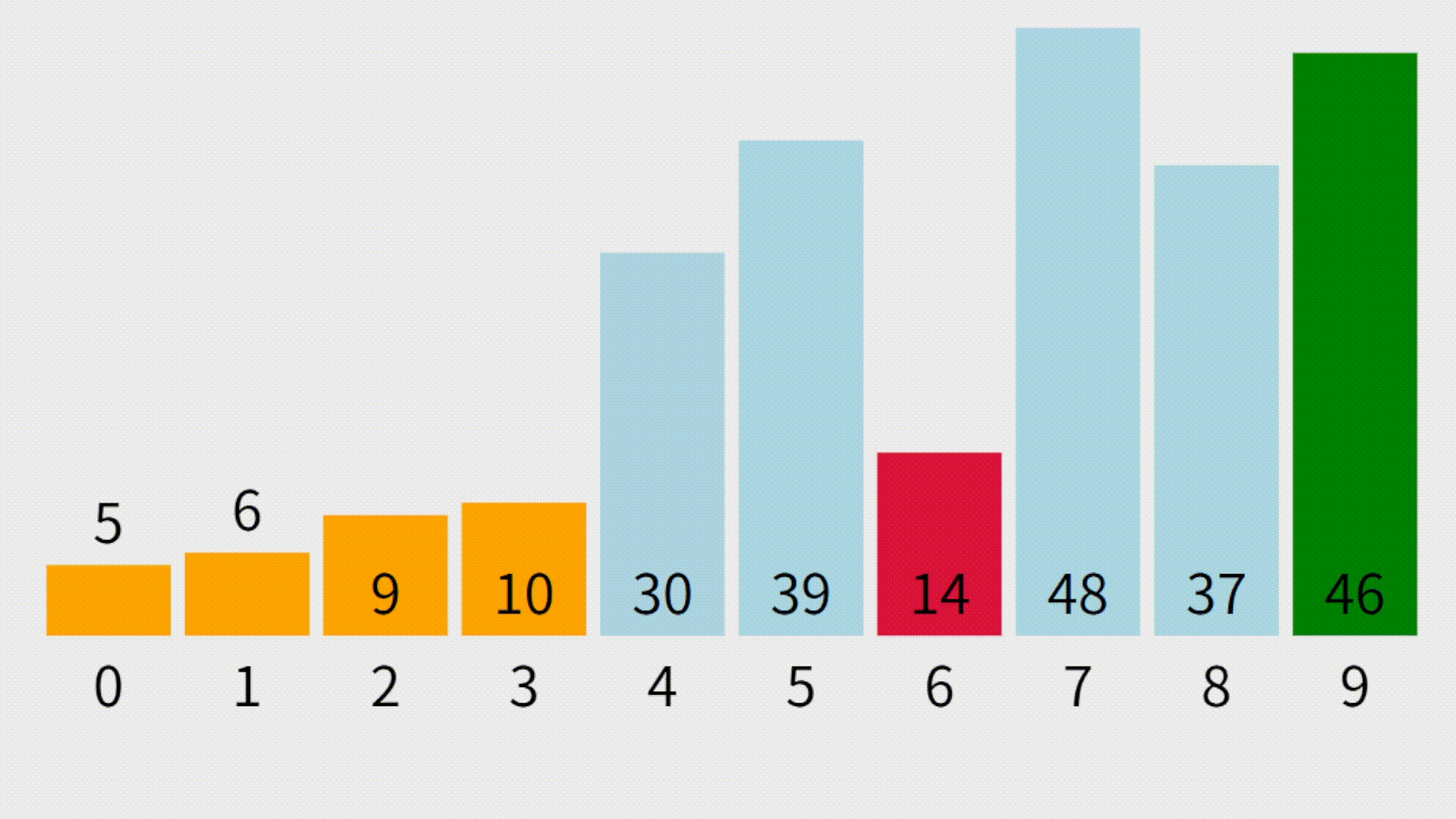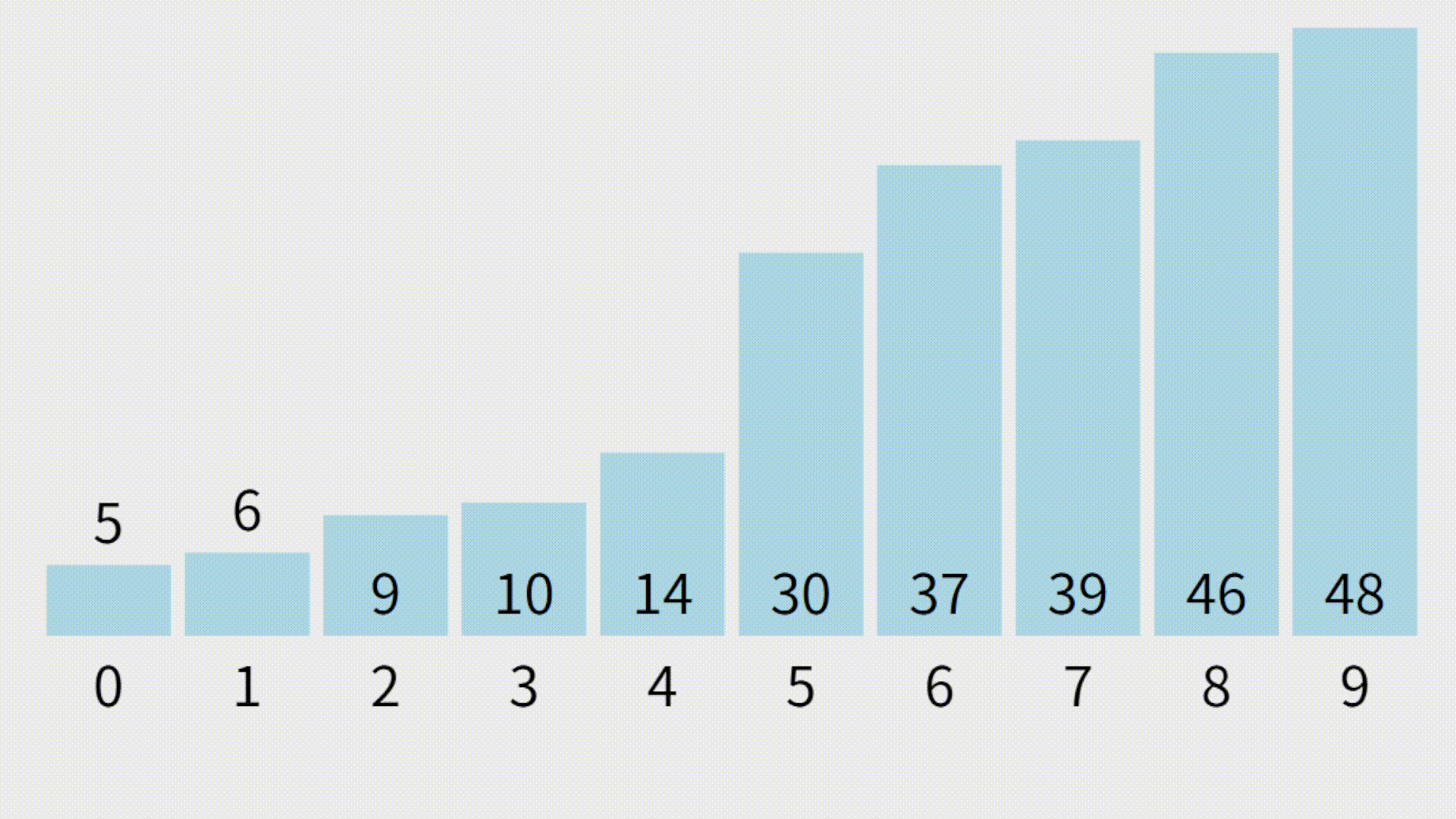
请添加图片描述

四、插入排序（Insertion Sort）

插入排序的核心思想是将数组分为 “已排序” 和 “未排序” 两部分，每次从 “未排序” 部分取一个元素，插入到 “已排序” 部分的正确位置，类似整理扑克牌的过程。

def insertion_sort(a,n):
    # 外层循环：控制未排序部分的元素（i 从 1 到 n-1，默认第一个元素为已排序部分）
    for i in range(1, n):
        # 记录当前待插入的元素
        current = a[i]
        # 内层循环：在已排序部分寻找插入位置（j 从 i-1 向前遍历）
        j = i - 1
        # 当已排序部分元素大于待插入元素时，将其向后移动
        while j >= 0 and a[j] > current:
            a[j + 1] = a[j]
            j -= 1
        # 将待插入元素放到正确位置
        a[j + 1] = current

`visualgo`演示动画

请添加图片描述

五、希尔排序（Shell Sort）

希尔排序是插入排序的改进版，核心思想是通过设定间隔（增量）将数组分割为多个子数组，对每个子数组进行插入排序，逐步缩小间隔直至为 1，最终完成整体排序。通过预排序减少数据的无序程度，提高最终插入排序的效率。

def shell_sort(arr):
    n = len(arr)
    # 初始间隔设为数组长度的一半，逐步缩小间隔
    gap = n // 2
    while gap > 0:
        # 对每个间隔组进行插入排序
        for i in range(gap, n):
            temp = arr[i]  # 当前待插入元素
            j = i
            # 间隔为gap的插入排序
            while j >= gap and arr[j - gap] > temp:
                arr[j] = arr[j - gap]
                j -= gap
            arr[j] = temp
        # 缩小间隔（通常取前一次的一半）
        gap //= 2
    return arr

`Algorithm Visualizer`演示动画

请添加图片描述

六、快速排序（Quick Sort）

快速排序是一种分治思想的排序算法，核心步骤为：选择一个 “基准值”，将数组分为 “小于基准值”“等于基准值”“大于基准值” 三部分，然后递归对左右两部分进行排序。通过分治策略大幅减少比较和交换次数，是实践中高效的排序算法之一。

def quick_sort(arr, left, right):
    if left >= right:
        return  # 子数组长度为1或0时无需排序
    # 选择基准值（此处选最左元素）
    pivot = arr[left]
    i, j = left, right
    # 分区操作：将小于基准值的放左边，大于的放右边
    while i < j:
        # 从右向左找第一个小于基准值的元素
        while i < j and arr[j] >= pivot:
            j -= 1
        arr[i] = arr[j]
        # 从左向右找第一个大于基准值的元素
        while i < j and arr[i] <= pivot:
            i += 1
        arr[j] = arr[i]
    # 将基准值放到最终位置
    arr[i] = pivot
    # 递归排序左子数组和右子数组
    quick_sort(arr, left, i - 1)
    quick_sort(arr, i + 1, right)

`visualgo`演示动画

请添加图片描述

七、归并排序（Merge Sort）

归并排序是一种基于分治思想的排序算法，核心思想是将数组递归拆分为两个子数组，分别排序后再合并为一个有序数组。通过 “分 - 治 - 合” 的策略，将复杂问题分解为简单子问题，最终实现整体排序。

# 1. 归并排序核心函数（递归实现）
def merge_sort(arr):
    # 基线条件：数组长度小于等于1时无需排序
    if len(arr) <= 1:
        return arr
    # 分：将数组拆分为左右两个子数组
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    # 合：将两个有序子数组合并为一个有序数组
    return merge(left, right)

# 2. 合并两个有序数组的函数
def merge(left, right):
    result = []
    i = j = 0
    # 比较两个子数组的元素，按从小到大顺序放入结果数组
    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    # 将剩余元素添加到结果数组（其中一个子数组已遍历完）
    result.extend(left[i:])
    result.extend(right[j:])
    return result

# 3. 读取输入并排序
n = int(input())
a = list(map(int, input().split()))
a = merge_sort(a)
print(' '.join(map(str, a)))

`visualgo`演示动画

请添加图片描述

八、桶排序（Bucket Sort）

桶排序是一种分布式排序算法，核心思想是将待排序数据分到若干个 “桶” 中，对每个桶内数据单独排序（可使用其他排序算法），最后将所有桶的结果合并。适用于数据分布均匀的场景，通过分桶减少单个桶内的数据量，从而提高排序效率。

#设置桶的默认数量为5
def bucket_sort_with_auto_size(arr, num_buckets = 5):
    if not arr or num_buckets <= 0:
        return arr.copy()
    # 1. 计算数据范围
    min_val = min(arr)
    max_val = max(arr)
    data_range = max_val - min_val
    # 2. 自动计算桶大小（确保每个桶的范围合理）
    # 处理所有元素都相同的特殊情况
    if data_range == 0:
        bucket_size = 1
    else:
        # 桶大小 = 数据范围 / 桶数量，向上取整确保覆盖所有数据
        bucket_size = (data_range + num_buckets - 1) // num_buckets
    # 3. 初始化桶
    buckets = [[] for _ in range(num_buckets)]
    # 4. 将元素分配到对应的桶中
    for num in arr:
        # 计算桶索引
        if data_range == 0:
            bucket_index = 0
        else:
            bucket_index = min((num - min_val) // bucket_size, num_buckets - 1)
        buckets[bucket_index].append(num)
    # 5. 桶内排序（使用插入排序）
    for bucket in buckets:
        for i in range(1, len(bucket)):
            current = bucket[i]
            j = i - 1
            while j >= 0 and bucket[j] > current:
                bucket[j + 1] = bucket[j]
                j -= 1
            bucket[j + 1] = current
    # 6. 合并所有桶的结果
    sorted_arr = []
    for bucket in buckets:
        sorted_arr.extend(bucket)
    
    return sorted_arr

`Algorithm Visualizer`演示动画

请添加图片描述

九、堆排序（Heap Sort）

堆排序是基于堆数据结构的排序算法，核心思想是先将数组构建为大顶堆（或小顶堆），然后反复提取堆顶元素（最大值或最小值）并调整堆结构，直至所有元素排序完成。利用堆的性质高效获取极值，实现整体排序。

def heap_sort(arr):
    n = len(arr)
    
    # 1. 构建大顶堆（从最后一个非叶子节点向上调整）
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)
    
    # 2. 逐步提取堆顶元素并调整堆
    for i in range(n - 1, 0, -1):
        arr[0], arr[i] = arr[i], arr[0]  # 交换堆顶（最大值）与当前末尾元素
        heapify(arr, i, 0)  # 调整剩余元素为大顶堆
    return arr

# 2. 堆调整函数（维护大顶堆性质）
def heapify(arr, n, i):
    largest = i  # 初始化最大值为根节点
    left = 2 * i + 1  # 左子节点索引
    right = 2 * i + 2  # 右子节点索引
    
    # 比较左子节点与当前最大值
    if left < n and arr[left] > arr[largest]:
        largest = left
    # 比较右子节点与当前最大值
    if right < n and arr[right] > arr[largest]:
        largest = right
    
    # 若最大值不是根节点，则交换并递归调整子树
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

# 3. 读取输入并排序
n = int(input())
a = list(map(int, input().split()))
a = heap_sort(a)
print(' '.join(map(str, a)))

`hufeifei`演示动画

为什么给链接不放gif?😠

听我解释：
找了一圈，发现还是这个演示动画最详细易懂，但是视频过长转gif内存太大了，导不进来。
加速的话感觉太快看不懂，有想剪辑一下添加字幕什么的，但是不知道怎么剪，压缩成GIF字幕很糊也看不清，最后只能给链接让读者自行跳转查看了😭

胡飞飞堆排序算法可视化

十、计数排序（Counting Sort）

计数排序是一种非比较型排序算法，核心思想是通过统计待排序元素中每个值出现的次数，然后根据次数计算每个值在结果数组中的位置，最终构建有序数组。适用于数据范围较小且为整数的场景，无需元素间比较即可完成排序。

def counting_sort(arr):
    if not arr:
        return arr    
    # 1. 确定数据范围（最大值和最小值）
    min_val = min(arr)
    max_val = max(arr)
    range_size = max_val - min_val + 1  # 数据范围大小
    
    # 2. 初始化计数数组并统计每个元素的出现次数
    count = [0] * range_size
    for num in arr:
        count[num - min_val] += 1  # 映射到计数数组索引（处理负数）
    
    # 3. 计算计数数组的前缀和（确定每个元素的结束位置）
    for i in range(1, len(count)):
        count[i] += count[i - 1]
    
    # 4. 反向遍历原数组，构建结果数组（保证稳定性）
    result = [0] * len(arr)
    for num in reversed(arr):
        # 计算当前元素在结果数组中的位置
        index = count[num - min_val] - 1
        result[index] = num
        count[num - min_val] -= 1  # 更新计数，确保重复元素位置正确
    return result

`Algorithm Visualizer`演示动画

请添加图片描述

十、基数排序（Radix Sort）

基数排序是一种非比较型排序算法，核心思想是按照低位到高位（或高位到低位）的顺序，对每个数位进行排序（通常使用计数排序作为子过程），逐步将所有数位排序完成，最终实现整体有序。利用数位的递进关系，通过多次子排序实现整体排序。

# 1. 基数排序核心函数（低位优先）
def radix_sort(arr):
    if not arr:
        return arr
    
    # 1. 确定最大数的位数（决定排序轮次）
    max_num = max(arr)
    digit_count = len(str(max_num))  # 数位数量
    
    # 2. 对每个数位进行计数排序（从低位到高位）
    for digit in range(digit_count):
        divisor = 10 ** digit  # 用于提取当前数位（1, 10, 100, ...）
        arr = counting_sort_by_digit(arr, divisor)
    return arr

# 2. 按指定数位进行计数排序（子过程）
def counting_sort_by_digit(arr, divisor):
    n = len(arr)
    result = [0] * n
    count = [0] * 10  # 0-9 共10个数字
    
    # 1. 统计当前数位的数字出现次数
    for num in arr:
        digit = (num // divisor) % 10
        count[digit] += 1
    
    # 2. 计算前缀和（确定每个数字的结束位置）
    for i in range(1, 10):
        count[i] += count[i - 1]
    
    # 3. 反向遍历原数组，构建结果数组（保证稳定性）
    for num in reversed(arr):
        digit = (num // divisor) % 10
        index = count[digit] - 1
        result[index] = num
        count[digit] -= 1
    return result

# 3. 读取输入并排序
n = int(input())
a = list(map(int, input().split()))
a = radix_sort(a)
print(' '.join(map(str, a)))

`visualgo`演示动画

请添加图片描述

十一、排序算法选型建议表

选型维度	推荐算法	推荐理由	不推荐算法	规避原因
小规模数据（n < 1000）	插入排序、选择排序	1. 插入排序：对接近有序数据友好，稳定且实现简单，局部调整效率高；2. 选择排序：交换次数仅 n-1 次，适合硬件交换成本高的场景（如元素体积大）	快速排序、归并排序	1. 快速排序：递归开销占比高，小规模数据下优势不明显；2. 归并排序：空间开销 O (n)，性价比低
中大规模数据（n ≥ 1000）	快速排序、归并排序	1. 快速排序：平均时间复杂度 O (n log n)，工业界常用，平均效率最高；2. 归并排序：复杂度稳定无退化，支持稳定排序和外排序（数据存磁盘）	冒泡排序、选择排序	时间复杂度 O (n²)，数据量增大时效率骤降，排序耗时呈平方级增长
需稳定排序	插入排序、归并排序、计数排序、基数排序、桶排序	1. 插入 / 归并排序：基于比较且稳定，适配多数数据类型；2. 计数 / 基数 / 桶排序：非比较型稳定排序，线性时间效率，适合特定场景（如整数、均匀分布数据）	选择排序、快速排序、堆排序	交换 / 分区 / 堆调整过程中，会改变相等元素的相对位置，无法保证稳定性
内存受限（低空间开销）	希尔排序、堆排序（迭代）、快速排序	1. 希尔排序：原地排序，空间复杂度 O (1)，无额外内存开销；2. 堆排序（迭代）：空间 O (1)，仅需常数级变量；3. 快速排序：平均空间 O (log n)，递归栈深度可控	归并排序、计数排序、桶排序	1. 归并排序：需 O (n) 空间存储合并结果；2. 计数 / 桶排序：需 O (n+k) 空间存储计数数组 / 桶
数据范围小（k ≈ n）	计数排序	线性时间复杂度 O (n+k)，直接统计元素出现次数，无需比较，效率远高于比较型排序	堆排序、快速排序	虽为 O (n log n) 复杂度，但需额外比较和逻辑处理，效率低于计数排序
数据均匀分布	桶排序	理想情况下时间复杂度 O (n)，按分布分桶后桶内元素少，排序开销低，可并行处理	选择排序、希尔排序	1. 选择排序：比较次数固定 O (n²)，不依赖数据分布；2. 希尔排序：效率受增量序列影响，均匀分布下无明显优势