作者:chen_h
微信号 & QQ:862251340
微信公众号:coderpai
(四)Python中随机森林的实现与解释
通过从单个决策树构建来使用和理解随机森林
幸运的是,对于像Scikit-Learn这样的库,现在很容易在Python中实现数百种机器学习算法。这很容易,我们通常不需要任何关于模型是如何工作的知识来使用它。虽然不需要知道所有细节,但了解机器学习模型如何工作仍然是非常有帮助的。这使我们可以在模型表现不佳时进行修改参数,或解释模型如何做出决策,如果我们想要说服别人相信我们的模型,这是至关重要的。
在本文中,我们将介绍如何在Python中构建和使用Random Forest。除了查看代码之外,我们还将尝试了解此模型的工作原理。因为由许多决策树组成的随机森林,我们首先要了解单个决策树如何对一个简单的问题进行分类。然后,我们将努力使用随机森林来解决现实世界的数据科学问题。
理解决策树
决策树是随机森林的构建块,是一种非常直观的模型。我们可以将决策树视为一系列对我们数据进行是/否分类的问题。这是一个可解释的模型,因为它可以像我们人类一样进行分类:在我们做出决定之前(在理想世界中),我们会询问有关可用数据的一系列查询,或者一系列特征。
在CART算法中,通过确定特征(称为节点的分裂)来构建决策树,这些特征在经过节点的时候通过Gini指数来进行判断。我们稍后会详细讨论关于Gini 指数的细节,但首先,让我们构建一个决策树,以便我们能够在高层次上理解它。
关于简单问题的决策树
我们将从一个非常简单的二分类问题开始,如下所示:

我们的数据只有特征,x1 和 x2,图中有 6 个数据样本,分为两个标签 0 和 1。虽然这个问题非常简单,但它是线性不可分的,这意味着我们不能通过数据绘制一条直线来对数据进行分类。
然而,我们可以绘制一系列直线,将数据点分成多个框,我们称之为节点。实际上,这就是决策树在训练期间所进行的操作。简单的说,决策树就是通过构造很多线性边界来构造的非线性模型。
为了创建决策树并在数据上进行训练,我们使用 sklearn 来进行。
from sklearn.tree import DecisionTreeClassifier
# Make a decision tree and train
tree = DecisionTreeClassifier(random_state=RSEED)
tree.fit(X, y)
在训练期间,我们为模型提供特征和标签,以便它可以根据特征进行学习,然后分类。然后,我们可以在训练数据上面对我们的模型进行测试。PS:因为我们没有测试数据。
print(f'Model Accuracy: {tree.score(X, y)}')
Model Accuracy: 1.0
我们看到它获得了100%的准确性,这也正是我们所期望的,因为我们给了它训练的数据,并且没有限制树的深度。 事实证明,完全学习训练数据的能力可能是决策树的缺点,因为它可能会导致过度拟合,这一点我们稍后会讨论。
可视化决策树
那么,当我们训练决策树时,实际上是在发生一些什么变化呢?我们找到一种可视化方法来理解决策树,我们可以通过 scikit-learn 中的函数,如下:
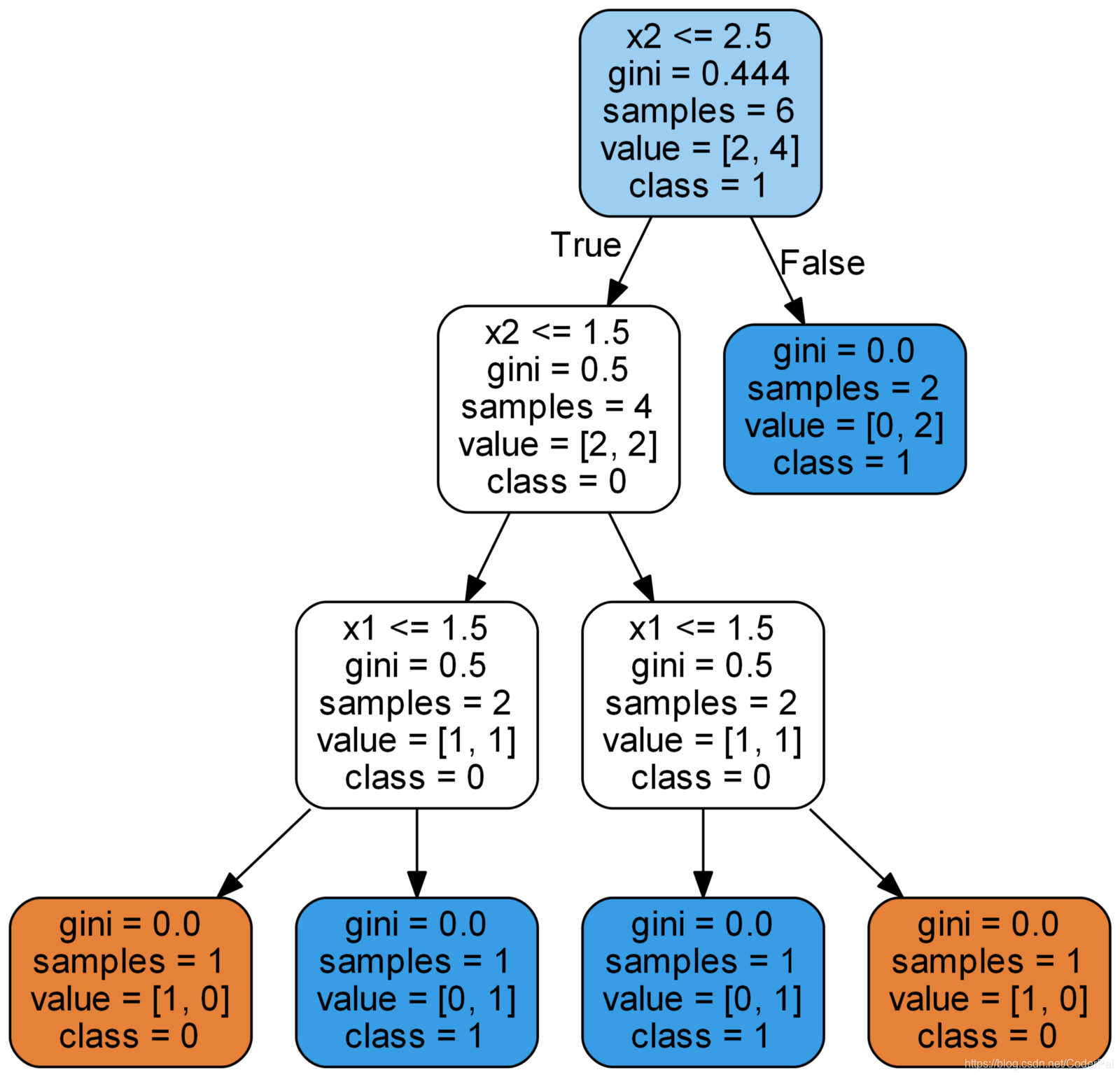
除了叶子节点,所有节点都有五个部分:
- 基于特征的查询,每个分裂节点都会给出真或者假的答案,根据答案,数据点向下移动到树上;
- gini:节点的 gini 指数。当我们向下移动时,平均加权的gini指数会减小;
- samples:节点中的观察数;
- value:每个类中的样本数。例如,顶部节点在类 0 中有2个样本,在类1中有4个样本;
- class:节点中点的多数分类。在叶子节点中,这就是对节点中所有样本的预测了;
对于叶子节点的理解肯定没有问题,因为这些是最终预测的地方。要对新的数据点进行分类,我们只需要将数据点进行下移就行了,使用点的特征来回答问题,直到到达类是预测的叶节点。
为了以不同的方式查看树,我们可以在原始数据上绘制决策树构建的分割。

每个拆分就是一条线,根据特征值将数据点划分为节点。对于这个简单的问题,我们并没有对最大深度进行限制,分区将节点中的每个点仅放置在同一类的点上。稍后我们将看到训练数据的这种完美划分可能不是我们想要的,因为它可能导致过度拟合。
gini 不纯度
在这一节上,我们会深入了解基尼不纯度的概念。节点的Gini不纯度是指节点中随机选择的样本如果被标记错误的概率,其实也就是节点中样本的分布。例如,在顶部节点中,Gini不纯度为 44.4% 。我们使用以下等式得出这个值:

节点 n 的Gini不纯度是 1 减去每个类概率平方的总和。这个听起来可能会有点困惑,那么我们就以根节点来做一个例子:

在每个节点处,决策树在特征中进行拆解,从而最大限度的减少GIni不纯度。
然后,它以贪婪的递归过程重复此拆分过程,直到达到最大深度,或者每个节点仅包含来自一个类的样本。 每层树木的加权总Gini不纯度必须减少。 在树的第二层,总加权基尼杂质值为0.333:

最终,最后一层的加权总 Gini 不纯度变为 0 ,意味着每个节点都是纯粹的,并且从该节点随机选择的点不会被错误分类。虽然这似乎是非常好的,但这意味着该模型可能过度拟合了,因为节点仅适用训练数据构建。
过度拟合:为什么森林比一棵树好
您可能会想问为什么不使用一个决策树?它似乎是完美的分类器,因为它没有犯任何错误!没有分错一个数据。但要记住的关键点是这个树是在训练数据上没有犯错。机器学习模型的目标是很好地概括它以前从未见过的新数据。
当我们具有非常灵活的模型(模型具有高容量)时,就会发生过度拟合,因为它基本上就是通过紧密拟合训练数据来生成模型的。问题是模型不仅学习训练数据中的实际关系,还学习任何存在的噪声。灵活模型具有高方差,因为学习参数(例如决策树的结构)将随着训练数据而显着变化。
另一方面,一个不灵活的模型被认为具有很高的偏差,因为它对训练数据做出了假设(它偏向于预先设想的数据思想。)例如,线性分类器假设数据是线性的,不具备适应非线性关系的灵活性。一个不灵活的模型可能无法适应训练数据,在这两种情况下,高方差和高偏差,那么模型无法很好地推广到新数据。
当我们不限制最大深度时,决策树非常容易过度拟合的原因是因为它具有无限的灵活性,这意味着它可以保持无限增长,直到它一个叶节点只有一个类别,完美地对所有这些进行分类。 如果您返回到决策树的图像并将最大深度限制为2(仅进行一次拆分),则分类不再100%正确。 我们减少了决策树的方差,但代价是增加了偏差。
我们为了限制树的深度,我们可以将许多决策树组合成称为随机森林的单个集合模型。那么就会减少方差(好)并增加偏差(差)。
随机森林
随机森林是由许多决策树组成的模型。 这个模型不是简单地平均树的预测(我们可以称之为“森林”),而是使用两个关键概念,使其名称为随机:
- 在构建树时对训练数据点进行随机抽样
- 分割节点时考虑的随机特征子集
随机抽样训练数据
在训练时,随机森林中的每棵树都会从数据点的随机样本中学习。 样本用替换采样,称为自举,这意味着一些样本将在一棵树中多次使用。 这个想法是通过对不同样本的每棵树进行训练,尽管每棵树相对于一组特定的训练数据可能具有很大的差异,但总体而言,整个森林的方差较小,但不会以增加偏差为代价。
在测试时,通过平均每个决策树的预测来进行预测。 这种在不同的数据子集上训练每个学习器然后对预测求平均值的过程称为bagging,是 bootstrap aggregating的缩写。
用于拆分节点的随机特征子集
随机林中的另一个主要概念是,仅考虑所有特征的子集来分割每个决策树中的每个节点。 通常,这被设置为sqrt(n_features)用于分类,这意味着如果有16个特征,则在每个树中的每个节点处,将仅考虑4个随机特征来分割节点。 (随机林也可以考虑每个节点的所有特征,在回归中比较常用。这些选项可以在Scikit-Learn Random Forest实现中控制)。
如果你能理解一个决策树,bagging的想法,以及随机的特征子集,那么你对随机森林的工作方式有了很好的理解:
随机森林将数百或数千个决策树组合在一起,在略微不同的训练集上训练每个决策树,考虑到有限数量的特征,在每棵树中分割节点。 随机森林的最终预测是通过平均每个树的预测来做出的。
要理解为什么随机森林优于单一决策树时,请想象以下情况:您必须决定特斯拉股票是否会上涨,并且您可以访问十几位对该公司没有先验知识的分析师。每个分析师都有较低的偏差,因为他们没有任何假设,并且可以从新闻报道的数据集中学习。
这似乎是一个理想的情况,但问题是报告除了真实信号之外可能还包含噪声。因为分析师完全根据数据做出预测 - 他们具有很高的灵活性 - 他们可能会被无关的信息所左右。分析师可能会从同一数据集中得出不同的预测。此外,如果给出不同的报告训练集,每个单独的分析师都有很大的差异,并会提出截然不同的预测。
解决方案是不依赖于任何一个人,而是汇集每个分析师的投票分析结果。此外,与随机森林一样,允许每个分析人员仅访问报告的一部分,并希望通过采样取消噪声信息的影响。在现实生活中,我们依赖于多种来源(绝不相信亚马逊的独立评论),因此,决策树不仅直观,而且在随机森林中将它们组合在一起的想法也是如此。
随机森林实践
接下来,我们将使用 Scikit-Learn 在 Python 中构建一个随机森林。 我们将使用分为训练和测试集的真实数据集,而不是学习一个简单的问题。 我们使用测试集作为模型对新数据的执行方式的估计,这也可以让我们确定模型过度拟合的程度。
数据集
我们要解决的问题是二元分类任务,其目标是预测个人的健康状况。 这些特征是个人的社会经济和生活方式特征,健康状况不佳的标签为0,健康状况为1。 该数据集由疾病控制和预防中心收集,可在此处获取(https://www.kaggle.com/cdc/behavioral-risk-factor-surveillance-system)。
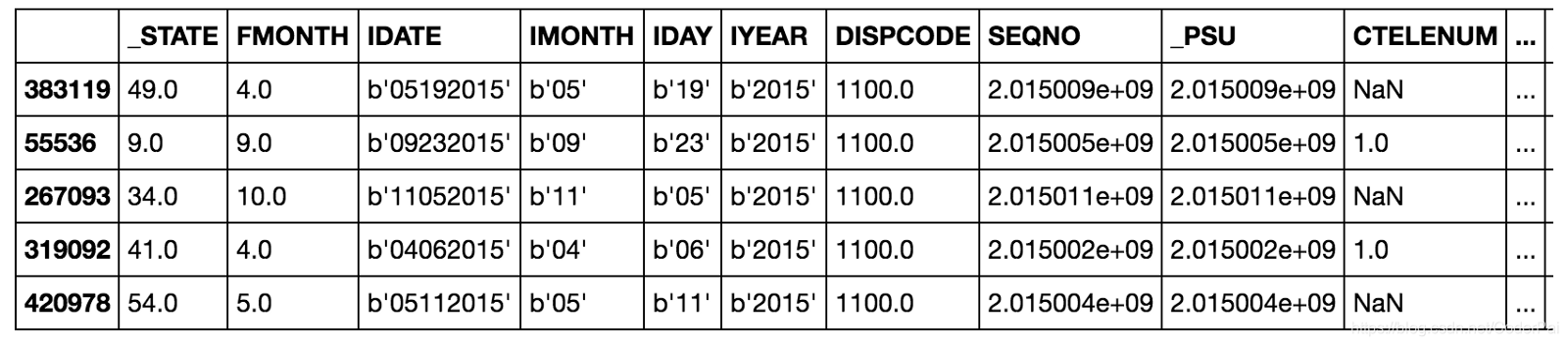
通常,数据科学项目的80%的时间用于清理,探索和制作数据中的特征。 但是,对于本文,我们将直接使用建模。 这是一个不平衡的分类问题,因此准确性不是一个合适的指标。 相反,我们利用 ROC AUC进行评估,从0(最差)到1(最佳)的度量,随机猜测得分为0.5。 我们还可以绘制ROC曲线以评估模型。
接下来我们开始学习随机森林代码,如下:
from sklearn.ensemble import RandomForestClassifier
# Create the model with 100 trees
model = RandomForestClassifier(n_estimators=100,
bootstrap = True,
max_features = 'sqrt')
# Fit on training data
model.fit(train, train_labels)
在训练几分钟后,模型准备好对测试数据进行如下预测:
# Actual class predictions
rf_predictions = model.predict(test)
# Probabilities for each class
rf_probs = model.predict_proba(test)[:, 1]
我们进行类别预测以及预测概率(predict_proba)来计算ROC AUC。 一旦我们有了测试预测,我们就可以计算出ROC AUC。
from sklearn.metrics import roc_auc_score
# Calculate roc auc
roc_value = roc_auc_score(test_labels, rf_probs)
结果
随机森林的最终测试ROC AUC为0.87,而具有无限最大深度的单一决策树的最终测试ROC AUC为0.67。 如果我们查看训练分数,两个模型都达到了1.0 的 ROC AUC,这也是预期的,因为我们给这些模型提供了训练标签,并没有限制每棵树的最大深度。
虽然随机森林过度拟合(在训练数据上比在测试数据上做得更好),但它能够比单一决策树更好地推广测试数据。 随机森林具有较低的方差(良好),同时保持决策树的相同低偏差(也很好)。
我们还可以绘制单个决策树(顶部)和随机森林(底部)的ROC曲线。 顶部和左侧的曲线是更好的模型:

上面是决策树的 ROC

上图是随机森林的 ROC
我们可以采用模型的另一个评估方法,混淆矩阵:
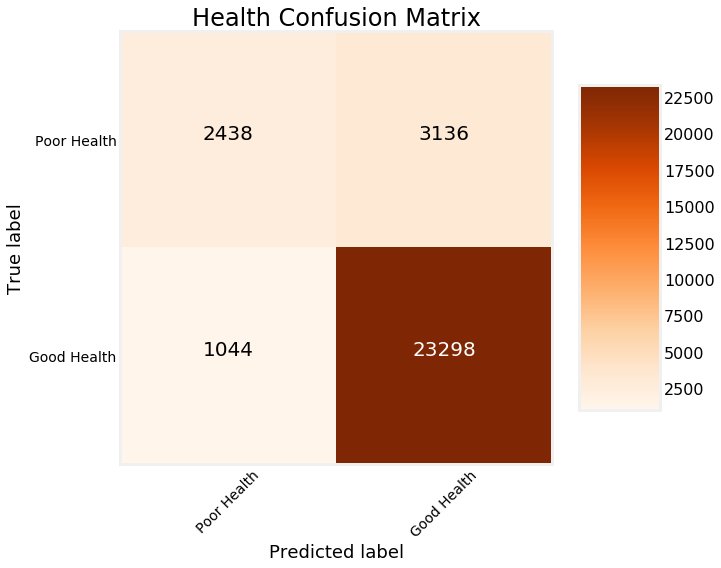
这显示模型在左上角和右下角正确的预测以及模型在左下角和右上角错误的预测。 我们可以使用这些图来诊断我们的模型,并确定它是否做得足够好以投入生产。
特征重要性
随机林中的特征重要性表示在该特征在拆分的所有节点上Gini不纯度减少的总和。 我们可以使用这些来尝试找出随机森林认为最重要的预测特征。 可以从训练好的随机森林中提取重要的特征,并将其放入Pandas数据框中,如下所示:
import pandas as pd
# Extract feature importances
fi = pd.DataFrame({'feature': list(train.columns),
'importance': model.feature_importances_}).\
sort_values('importance', ascending = False)
# Display
fi.head()
feature importance
DIFFWALK 0.036200
QLACTLM2 0.030694
EMPLOY1 0.024156
DIFFALON 0.022699
USEEQUIP 0.016922
特征重要性告诉我们哪些特征在类之间最具辨别力,可以让我们深入了解问题。 例如,这里指示患者是否行走困难的 DIFFWALK 特征是最具有意义的特征。
通过构建最重要的特征分析,我们可以通过删除低重要性的特征,使用高重要性的特征来进行学习。
可视化随机森林
最后,我们可以在森林中可视化单个决策树。 这次,我们必须限制树的深度,否则它将太大而无法转换为图像。 为了得到下图,我将最大深度限制为6.这仍然导致我们无法完全解析大树! 然而,鉴于我们深入研究决策树,我们掌握了模型的工作原理。

 随机森林实战
随机森林实战





















 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








