有效的完全平方数

最新推荐文章于 2022-03-29 22:45:00 发布

原创最新推荐文章于 2022-03-29 22:45:00 发布 · 235 阅读

0 ·

CC 4.0 BY-SA版权

C++ 专栏收录该内容

76 篇文章

订阅专栏

本文介绍了一种使用牛顿迭代法求解平方根的方法。通过解析切线方程，推导出了迭代公式(xi+1)=(xi+n/xi)/2，并给出了C++实现代码，用于判断一个数是否为完全平方数。

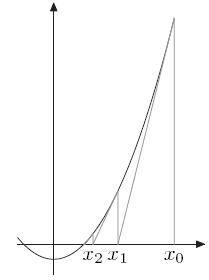
在这里插入图片描述
经过(xi, f(xi))这个点的切线方程为f(x) = f(xi) + f’(xi)(x - xi)，
其中f’(x)为f(x)的导数，本题中为2x。令切线方程等于0，即可求出xi+1=xi - f(xi) / f’(xi)。
继续化简：

xi+1
=xi - (xi2 - n) / (2xi)
= xi - xi / 2 + n / (2xi
= xi / 2 + n / 2xi
= (xi + n/xi) / 2。

class Solution {
public:
    bool isPerfectSquare(int num) {
        long long start = num;
        while(start * start > num)
        {
            start = (start + num/start)/2;
        }
        if (start * start == num)
            return true;
        return false;
    }
};