Jerry Mouse
Time Limit: 1000ms Memory limit: 65536K 有疑问?点这里^_^
题目描述
Kudo and Saya are good friends, and they are always together.
But today, since Saya is not here (Where is Saya? You can get the answer at Problem F), Kudo fells very bored. So Kudo starts to watch TV for fun.
Now, she is watching the famous cartoon “Tom and Jerry”. Jerry’s home have many entrance, he always enter his home in an entrance and get out from another.
Kudo suddenly thought that what will happen if there are many Jerrys?
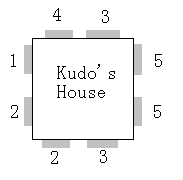
Kudo finds out a paper box and dig many holes in the side of the box. Then, she marks every hole with an integer, representing its owner. Finally, she signs the box “Kudo’s House” as shown in Figre 1.
She defined mouse A and mouse B is the same mouse if and only if:
a) mouse A and mouse B are in a same house and A equals to B;
b) mouse A and mouse B are in different houses, but they have a hole that combined together, such as mouse 3 in Kudo’s House and mouse 7 in Lin’s House;
c) There exits a lists of mouse M1, M2 … Mp, while A and M1 are the same, M1 and M2 are the same … Mp and B are the same.
But there is a problem: Suppose mouse 3 in Kudo’s House is the same with mouse 7 in Lin’s House, while mouse 7 in
Lin’s House is the same with mouse 4 in Kudo’s House. It means that mouse 3 and 4 in Kudo’s House are the same!
Kudo is very confused, so she comes to you for help.
Given the initial N boxes, can you tell her finally each hole belongs to whom?
Here, N always equals to 1, 4, 9, 16, 25, 36, 49, 64, 81 or 100. Kudo always combines the boxes as shown in Figure 3, while n = √N.
But today, since Saya is not here (Where is Saya? You can get the answer at Problem F), Kudo fells very bored. So Kudo starts to watch TV for fun.
Now, she is watching the famous cartoon “Tom and Jerry”. Jerry’s home have many entrance, he always enter his home in an entrance and get out from another.
Kudo suddenly thought that what will happen if there are many Jerrys?
Kudo finds out a paper box and dig many holes in the side of the box. Then, she marks every hole with an integer, representing its owner. Finally, she signs the box “Kudo’s House” as shown in Figre 1.

Figure 1 The gray part represents a hole, and the numbers means its owner, i.e. the two gray parts in the lower left corner means the two holes belongs to mouse 2.
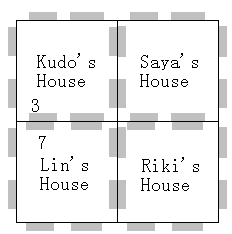
Kudo think it is very interesting, so she makes a lot of boxes, and sign them “Saya’s House”, “Riki’s House”, “Lin’s House” and so on.

Figure 2 The jointed gray parts represent the same hole.
At last, she combines them together to make a large box as shown in Figure 2.She defined mouse A and mouse B is the same mouse if and only if:
a) mouse A and mouse B are in a same house and A equals to B;
b) mouse A and mouse B are in different houses, but they have a hole that combined together, such as mouse 3 in Kudo’s House and mouse 7 in Lin’s House;
c) There exits a lists of mouse M1, M2 … Mp, while A and M1 are the same, M1 and M2 are the same … Mp and B are the same.
But there is a problem: Suppose mouse 3 in Kudo’s House is the same with mouse 7 in Lin’s House, while mouse 7 in
Lin’s House is the same with mouse 4 in Kudo’s House. It means that mouse 3 and 4 in Kudo’s House are the same!
Kudo is very confused, so she comes to you for help.
Given the initial N boxes, can you tell her finally each hole belongs to whom?
Here, N always equals to 1, 4, 9, 16, 25, 36, 49, 64, 81 or 100. Kudo always combines the boxes as shown in Figure 3, while n = √N.
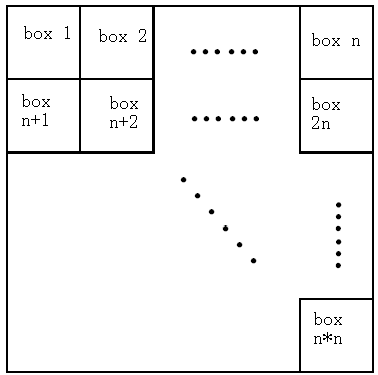
Figure 3 How Kudo combines the boxes.
输入
The input consists of several test cases.
The first line of input in each test case contains two integers N (0<N≤100) and M (0<M≤1000), which represent the number of boxes and the number of holes in each side of the box. In every side of the N boxes,You can assume that there are always M holes, and the M holes are arranged with equal spacing.
Each of the next N lines containing 4M integers representing the holes on the boxes. The first M integers represent the holes on the upside, from left to right; the second M integers represent the holes on the downside, from left to right; the third M integers represent the holes on the leftward, from up to down; the forth M integers represent the holes on the rightward, from up to down. You can assume that the hole number is not greater than M*2.
The last case is followed by a line containing two zeros.
The first line of input in each test case contains two integers N (0<N≤100) and M (0<M≤1000), which represent the number of boxes and the number of holes in each side of the box. In every side of the N boxes,You can assume that there are always M holes, and the M holes are arranged with equal spacing.
Each of the next N lines containing 4M integers representing the holes on the boxes. The first M integers represent the holes on the upside, from left to right; the second M integers represent the holes on the downside, from left to right; the third M integers represent the holes on the leftward, from up to down; the forth M integers represent the holes on the rightward, from up to down. You can assume that the hole number is not greater than M*2.
The last case is followed by a line containing two zeros.
输出
For each case, print the case number (1, 2 …) and 4*n*M integers (n=√N) represents the holes on the upside, downside, leftward and rightward side of the large box, using the same format as the input file.
In your answer, the holes signed by the same numbers should belong to the same mouse, while the holes signed by different numbers should belong to different mouse. The number should be an integer, starting from 1. Since there are multiply solutions, please print the one whose first number is the least. If there are still multiply solutions, print the one whose second number is the least, and so on.
Your output format should imitate the sample output. Print a blank line after each test case.
In your answer, the holes signed by the same numbers should belong to the same mouse, while the holes signed by different numbers should belong to different mouse. The number should be an integer, starting from 1. Since there are multiply solutions, please print the one whose first number is the least. If there are still multiply solutions, print the one whose second number is the least, and so on.
Your output format should imitate the sample output. Print a blank line after each test case.
示例输入
4 1 2 2 1 1 2 2 1 1 1 1 2 2 1 1 2 2 0 0
示例输出
Case 1: 1 2 1 2 3 4 3 4
 卡通老鼠游戏谜题
卡通老鼠游戏谜题





 本博客介绍了一款基于卡通角色“汤姆与杰瑞”的趣味编程挑战,玩家需要解决多个小老鼠之间的连通性问题,通过一系列规则判断哪些老鼠被视为同一个个体。游戏设定在一个由多个盒子组合而成的大盒子中,每个盒子都有多个入口,并标记了不同的数字来表示其归属。挑战在于理解这些规则并找出最终每个入口归属于哪个个体。
本博客介绍了一款基于卡通角色“汤姆与杰瑞”的趣味编程挑战,玩家需要解决多个小老鼠之间的连通性问题,通过一系列规则判断哪些老鼠被视为同一个个体。游戏设定在一个由多个盒子组合而成的大盒子中,每个盒子都有多个入口,并标记了不同的数字来表示其归属。挑战在于理解这些规则并找出最终每个入口归属于哪个个体。
















 2160
2160

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








