leetcode刷题知识点

知识点整理：

一、数组

1、求数组长度

sizeof(arr1) / sizeof(arr1[0]);

结果是三维数组的空间申请：

        char*** res = (int **)malloc(sizeof(char**) * stringsSize);
        for (int i = 0; i < stringsSize; i++) {
            res[i] = (char**)malloc(stringsSize * sizeof(char*));
            for (int j = 0; j < stringsSize; j++) {
                res[i][j] = (char*)malloc(sizeof(char*) * 26);
                memset(res[i][j], 0, sizeof(char*) * 26);
            }
        }

或者

    /* 初始化 */
    char*** ret = (char***)malloc(sizeof(char**) * stringsSize);
    *returnColumnSizes = (int*)malloc(sizeof(int) * stringsSize);
    for (int i = 0; i < stringsSize; i++) {
        ret[i] = (char**)malloc(sizeof(char*) * stringsSize);
        (*returnColumnSizes)[i] = 0;
    }

二、字符串

sscanf（src，format，dst）

string ————> string

	   ————> int

代替atoi

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int main()
{
   int day, year;
   char weekday[20], month[20], dtm[100];

   strcpy( dtm, "Saturday March 05:1989" ); //不受中间的字符的影响
   sscanf( dtm, "%s %s %d:%d", weekday, month, &day, &year ); // itoa

   printf("%s %d, %d = %s\n", month, day, year, weekday );
    
   return(0);
}

常见用法：

取指定长度的字符串。如在下例中，取最大长度为4字节的字符串。
sscanf(“123456 “, “%4s”, buf);
printf(”%s\n”, buf);
结果为：1234

参考：https://www.cnblogs.com/lyq105/archive/2009/11/28/1612677.html

sprintf（dst, format, src）

snprintf（dst, size, format, src）

    char* s = "runoobcom";
 
    // 读取字符串并存储在 buffer 中
    int j = snprintf(buffer, 6, "%s\n", s); // atoi

	//buffer:"runoo"(其中有个结束符)
	//j = 10,原字符串长度

strcmp

strncmp

strcpy

strncpy

strstr

返回第一次出现子串substr的地址；如果没有检索到子串，则返回NULL

   const char haystack[20] = "RUNOOB";
   const char needle[10] = "NOOB";
   ret = strstr(haystack, needle);
 
   printf("子字符串是： %s\n", ret);
	// 子字符串是： NOOB

strtok

token = strtok(str, s) // str 字符串， s是间隔符
while(token != NULL) {
    token = strtok(NULL, s);
}

三、排序

qsort模板：
参考https://leetcode-cn.com/circle/article/KBnaqU/

//一、一维数组
/* 升序 */
int cmp(const void* a, const void* b) {
    return (*(int*)a - *(int*)b);
}

//二、二维数组 维度m*2
/* 1、直接定义成数组 */
int cmp1(const void* a, const void* b) {
    int *m =(int*)a, *n =(int*)b; //一级指针代表一级数组
    if (m[0] != n[0]) {
        return (m[0] - n[0])
    } else {
        return (m[1] - n[1]);
    }
}

/* 2、动态分配内存 */
int cmp2(const void* a, const void* b) {
    int *m = *(int**)a, *n = *(int**)b;
    if (m[0] != n[0]) {
        return m[0] - n[0];
    } else {
        return m[1] - n[1];
    }
}
int **arr2 = (int**)malloc(sizeof(int*) * 10);
for (int i = 0; i < 10; i++) {
    arr2[i] = (int*)malloc(sizeof(int) * 2);
    memset(arr2[i], 0, sizeof(int) * 2);
}
qsort(arr2[i], 10, sizeof(int*), cmp2);

//三、二维数组 维度m*n
/* 1、直接定义成数组 */
#define MAX 3
int cmp1(const void* a, const void* b) {
    int *m = (int*)a, *n = (int*)b;
    for (int i = 0; i < MAX; i++) {
        if (m[i] != n[i]) {
            return m[i] - n[i];
        }
    }
}

/* 2、动态分配内存 */
int cmp2(const void* a, const void* b) {
    int *m = *((int**)a), *n = *((int**)b);
    for (int i = 0; i < MAX; i++) {
        if (m[i] != n[i]) {
            return m[i] - n[i];
        }
    }
}

//三、字符串(字符数组)
int cmp(const void* a, const void *b) {
    return strcmp((char*)a, (char*b));
}

//四、字符串数组
/* 1、直接定义成数组 */
int cmp1(const void *a, const void *b) { //a是str1中的元素 与qsort(str1)是一种类型，类型对齐
    return strcmp((char*)a, (char*)b);
}
int cmp2(const void* a, const void *b) {
    return strcmp(*(char**)a, *(char**)b);
}
char str1[][10] = { "iosd", "adw", "werws", "sdf", "abc" }; //字符串数组 qsort(str1) str1看做一维数组 str1是一级指针
char *str2[] = { "iosd", "adw", "werws", "sdf", "abc" }; //字符串指针数组qsort(str2) str2看做二维数组 str2是二级指针
char **str3 = (char**)malloc(sizeof(char*) * 5);
for (int i = 0; i < 5; i++) {
	str3[i] = malloc(sizeof(char) * 26);
}
qsort(str1, 5, sizeof(str1[0]), cmp1);
qsort(str2, 5, sizeof(char*), cmp2);
qsort(str3, 5, sizeof(char*), cmp2);

//五、数据结构数组
/* ①根据字符串长度进行排序；②字符串长度相同时，根据字符串字符对应ascii值进行排序 */
struct STR {
    int len;
    char *str;
};

int cmp(const void *a, const void *b) {  //cmp的写法比较灵活，可以根据排序需要进行修改
    struct STR *m = (struct STR*)a, *n = (struct STR*)b;
    if (m->len != n->len) {
        return m->len - n->len;
    }
    else {
        return strcmp(m->str, n->str);
    }
}

int main() {
    char *str[8] = { "acd", "fsfe", "aae", "sw", "servb", "fsvbs", "wg" };  //题目给定的字符串序列

    struct STR *arr = (struct STR*)calloc(8, sizeof(struct STR));
    for (int i = 0; i < 7; i++) {  //对结构体len和str进行赋值
        arr[i].len = strlen(str[i]);
        arr[i].str = (char*)calloc(10, sizeof(char));
        strcpy(arr[i].str, str[i]);
    }

    qsort(arr, 7, sizeof(struct STR), cmp);
}

作者：雨不落
链接：https://leetcode-cn.com/circle/article/KBnaqU/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
 
//--浮点
//　在对浮点或者double型的一定要用三目运算符，因为要是使用像整型那样相减的话，如果是两个很接近的数则可能返回一个很小的小数
//（大于-1，小于1），而cmp的返回值是int型，因此会将这个小数返回0，系统认为是相等，失去了本来存在的大小关系
int compare (const void *a, const void *b) {
    return *(double*)a > *(double*)b ? 1 : -1;//不能直接写 return *(double*)a - *(double*)b
}

//总结
/* 
1、 普通数组定义，如int arr[10][2]、char str[10][5]的方式定义的二维数组或字符串数组
*/
int cmp(const void *a, const void *b)
{
    char *m = (int*)a, *n = (int*)b;
    return ;
}
qsort(arr, 10, arr[0], cmp);
/* 
2、 指针数组定义，如int **arr =(int**)calloc(...)、char *str[10]的方式定义的指针数组
*/
int cmp(const void *a, const void *b)
{
    char *m = *(int**)a, *n = *(int**)b;
    return ;
}
qsort(arr, 10, sizeof(int*), cmp);

四、二分查找

闭区间统一模板：

// 只存在一个target
/* 二分搜索 */
int search(int* nums, int numsSize, int target){
    int left = 0;
    int right = numsSize - 1;
    int mid;
    while (left <= right) {
        mid = left + (right - left) / 2;
        if (target == nums[mid]) {
            return mid;
        } else if (target < nums[mid]) {
            right = mid - 1;
        } else if (target > nums[mid]){
            left = mid + 1;
        }
    }
    return -1;
}
// 存在多个target
/* 二分搜索 边界 */
int left_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定左侧边界
            right = mid - 1;
        }
    }
    // 最后要检查 left 越界的情况
    if (left >= nums.length || nums[left] != target) {
        return -1;
    }
    return left;
}

int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定右侧边界
            left = mid + 1;
        }
    }
    // 最后要检查 right 越界的情况
    if (right < 0 || nums[right] != target) {
        return -1;
    }
    return right;
}

五、设计题

结构体定义

顺序表

typedef struct {
    int len;
    char str[MAX]; //字符串元素尽量使用静态，浪费空间，但不需要再动态申请
}

链表

typedef struct SNode{
  struct ListNode *head;
  int length;
} Solution;

顺序表几个步骤

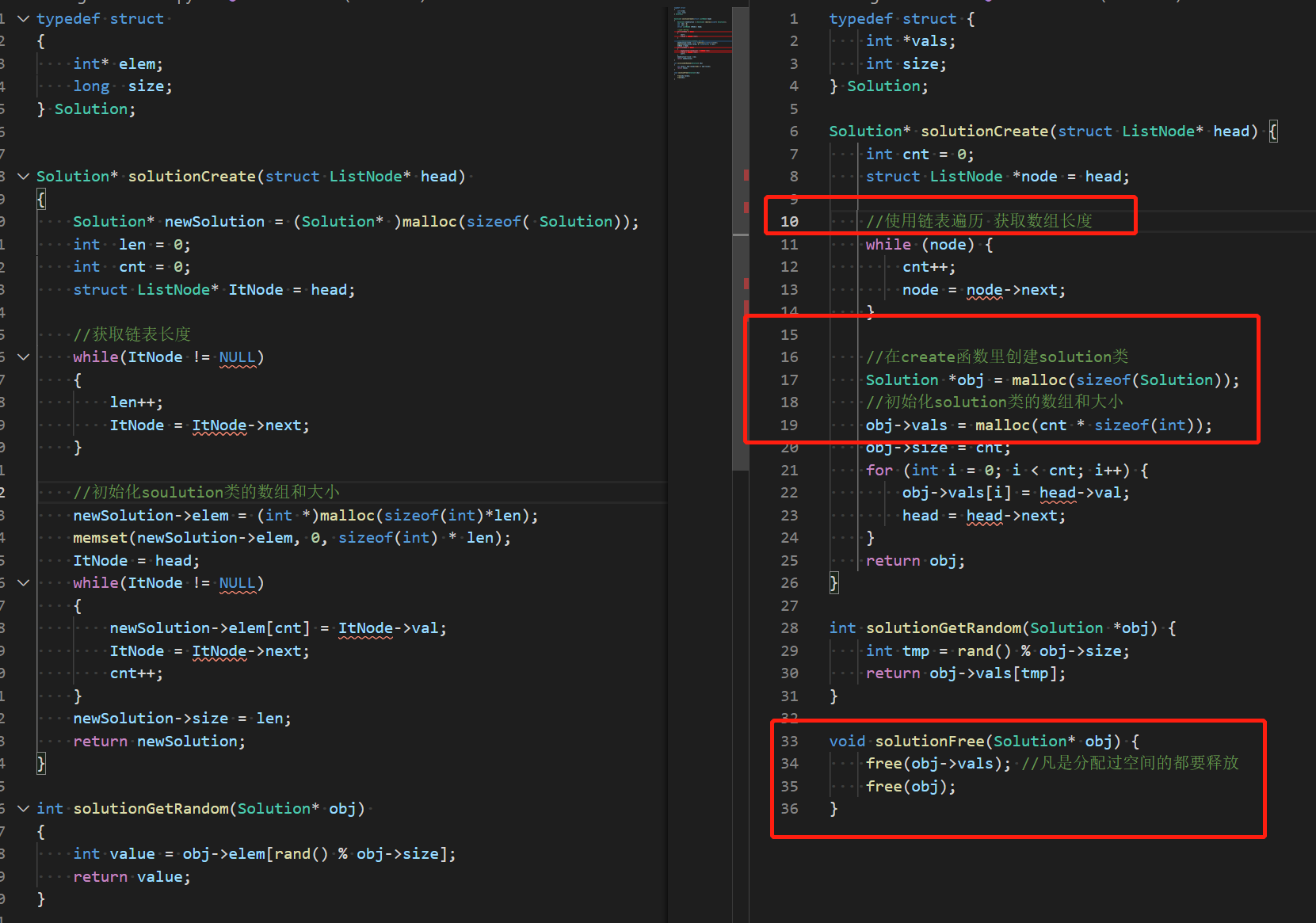
初始化：359题与382题对比

访问方式

. 和 ->

obj[i].message 是因为obj[i]是顺序表的结点

obj->vals[i] 是因为obj是顺序表头指针

初始化

obj[i].val = val;

strcpy(obj[i].message, message);

1396. 设计地铁系统

不要在添加结点的时候使用循环，因为会多次调用

//错误用法：在增加结点时，使用了循环，忽略结点是多次调用的
void undergroundSystemCheckIn(UndergroundSystem* obj, int id, char * stationName, int t) {
    for (int i = 0; i < MAX; i++) {
        obj[i].id = id;
        strcpy(obj[i].startStation, stationName);
        obj[i].t1 = t;
    }
    return;
}

//正确做法
int top = 0; //定义全局变量
void undergroundSystemCheckIn(UndergroundSystem* obj, int id, char * stationName, int t) {
    obj[top].id = id;
    strcpy(obj[top].startStation, stationName);
    obj[top].t1 = t;
 	top++;
    return;
}

如果定义了全局变量top，来表示事件调用次数，需要在对象创建阶段将其置0
752. 打开转盘锁

#define NUMMAX 1001
typedef struct {
    int time[2];
    //int index;
} MyCalendar;

int top = 0; // 如果结构体当中有记录长度的index就不需要top了

MyCalendar* myCalendarCreate() {
    top = 0;    // 需要在每次测试用例调用之前进行清零，否则多次调用，top一直累加会越界
    MyCalendar* myCalendar = (MyCalendar*)malloc(sizeof(MyCalendar) * NUMMAX);
    for (int i = 0; i < NUMMAX; i++) {
        myCalendar[i].time[0] = 0;
        myCalendar[i].time[1] = 0;
    }
    return myCalendar;
}

uthash库的使用

1）使用场景：

1. key-val键值对关系
2. 题目中需要查找key来填充val

2）初始化

typedef struct {
	int key;
	int val;
	UT_hash_handle hh; // 哈希表内部的一个句柄，一定要包含
} HashTable;

HashTable* g_usrs = NULL; // 初始化全局指针，指向整个hash表
int top; // 哈希表结点的长度

HashTable* HashTableCreate(int capacity) {
	top = capacity;
	return g_usrs;
}

3）添加（包含“查找”）

void HashTablePut(HashTable* obj, int key, int value) {
	HashTable* cur_usr = NULL;
	/* 重复性检查，当把两个相同的key值的结构体添加到哈希表会报错 */
	HASH_FIND_INT(g_usr, &key, cur_usr);
	if (cur_usr == NULL) {
		cur_usr = (HashTable*)malloc(sizeof(HashTable)); // 指针不为空，记得分配空间
		cur_usr->key = key;
		cur_usr->val = val;
		HASH_ADD_INT(g_usrs, key, cur_usr);
	}
}

4） 循环删除

void HashTableDelete() {
	HashTable* cur_usr = NULL;
	HashTable* next_usr = NULL;
	HASH_ITER(hh, g_usr, cur_usr, next_usr) {
		HASH_DEL(g_usr, cur_usr);
		free(user); // 可选
	}
}

uthash库函数汇总：

HASH_ADD_INT(g_usr, key, cur_usr); // 增加
HASH_FIND_INT(g_usr, &key, cur_usr); // 查找
HASH_DEL(g_usr, cur_usr);	// 删除
HASH_ITER(hh, g_usrs, cur_usr, next_usr); // 迭代
HASH_COUNT(g_usrs); // 计数
HASH_SORT(g_usrs, cmp); // cmp与qsort中的比较函数完全一致

/* 遍历哈希表中的所有项目 */
// 法一：使用哈希表中的句柄递归打印
for(s=users; s != NULL; s=s->hh.next) {
        printf("user id %d: name %s\n", s->id, s->name);
        }
// 法二：
HASH_ITER(hh, g_usrs, cur_usr, next_usr) {
	printf("user id %d: name %s\n", s->id, s->name);
}

六、前缀和、差分

前缀和

1）使用场景：
一维前缀和：
适用于快速、频繁地计算一个索引区间内的元素之和。计算i~j对应的元素之和，sum[i…j] = sum[j + 1] - sum[i]
二维前缀和：
计算矩形面积
2）核心代码
图示：
nums 3 5 2 -2 4 1
preSum 0 3 8 10 8 12 13
如果要求索引区间[1, 4]内的所有元素之和，就可以通过preSum[5] - preSum[1]，时间复杂度为O(1)。

/* 构造前缀和数组 */
int* presum = (int*)malloc(sizeof(int) * (numsSize + 1)); // 会比原来的数组多一个值
preSum[0] = 0 // preSum[0] = 0, 便于计算累加和
for (int i = 1; i < numsSize; i++) {	
	preSum[i] = preSum[i - 1] + nums[i - 1];
}

/* 计算nums中i ~ j的和 */
int ans = preSum[j + 1] - preSum[i];

差分

1）使用场景
差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。
2）核心代码
图示：
nums 8 2 6 3 1
diff 8 -6 4 -3 -2
如果对nums数组1~3的区间进行+3，等价于在diff数组索引1加3，而对索引4减3

/* 构造差分数组 */
int* diff = (int*)malloc(sizeof(int) * numsSize);
diff[0] = nums[0]
for (int i = 1; i < numsize; i++) {
	diff[i] = nums[i] - nums[i - 1];
}
/* 对区间增减后求原数组 */
diff[i] += val;
if (j + 1 < numsSize) {
	diff[j + 1] -= val;
}

七、滑动窗口

算法应用场景：

关键词：

满足xxx条件（计算结果，出现次数，同时包含）

最长/最短

子串/子数组/子序列

例如：长度最小的子数组

滑动窗使用思路（寻找最长）

——核心：左右双指针（L，R）在起始点，R向右逐位滑动循环

——每次滑动过程中

如果：窗内元素满足条件，R向右扩大窗口，并更新最优结果

如果：窗内元素不满足条件，L向右缩小窗口

——R到达结尾

滑动窗使用思路（寻找最短）

——核心：左右双指针（L、R）在起始点，R向右逐位滑动循环

——每次滑动的过程中

如果：窗内元素满足条件，L向右缩小窗口，并更新最优结果

如果：窗内元素不满足条件，R向右扩大窗口

——R到达结尾

//最长模板
初始化left,right,result,bestResult
while (右指针没有到结尾) {
    窗口扩大，加入right对应元素，更新当前result
    while(result不满足要求) {
        窗口缩小，移除left对应元素，left左移
    }
    更新最优结果bestResult
    right++;
}
返回bestResult;

//最短模板
初始化left,right,result,bestResult
while (右指针没有到结尾) {
    窗口扩大，加入right对应元素，更新当前result
    while(result满足要求) {
        更新最优结果bestResult
        窗口缩小，移除left对应元素，left左移
    }
    right++;
}
返回bestResult;

八、二叉树

二叉树遍历（递归）

前、中、后

递归三要素：

1.确定递归函数的参数和返回值

2.确定终止条件

3.确定单层递归逻辑

#define MAX 2000
// 前序
// 1.确定递归函数的参数和返回值
void preorder(struct TreeNode* root, int* ret,int* returnSize)
{
    // 2.确定终止条件
    if (root == NULL) {
        return;
    }
    // 3.确定单层递归逻辑
    ret[(*returnSize)++] = root->val;
    preorder(root->left, res, returnSize);
    preorder(root->right, res, returnSize);
    return;
}
// 中序
void middleorder(struct TreeNode* root, int* ret,int* returnSize) {
    if (root == NULL) {
        return;
    }
    middleorder(root->left, res, returnSize);
    ret[(*returnSize)++] = root->val;
    middleorder(root->right, res, returnSize);
    return;
}
// 后序
void postorder(struct TreeNode* root, int* ret,int* returnSize) {
    if (root == NULL) {
        return;
    }
    postorder(root->left, res, returnSize);
    postorder(root->right, res, returnSize);
    ret[(*returnSize)++] = root->val;
    return;
}
int* Travsersal(struct TreeNode* root, int* returnSize) {
    int *ret = malloc(sizeof(int) * MAX);
    *returnSize = 0;
    preorder(root, res, returnSize);
    middleorder(root, res, returnSize);
    postorder(root, res, returnSize);
    
    return ret;
}

二叉树遍历（非递归 栈）

// 前序
#define MAX 100
int* preorderTraversal(struct TreeNode* root, int* returnSize){
    int* ret = (int*)malloc(sizeof(int) * MAX);
    struct TreeNode** stk = (struct TreeNode**)malloc(sizeof(struct TreeNode) * MAX);
    *returnSize = 0;
    int top = -1;
    struct TreeNode* p = root;
    while(p != NULL || top > -1) {
        if (p != NULL) {
            ret[(*returnSize)++] = p->val;
            stk[++top] = p;
            p = p->left;
        } else {
            p = stk[top--]->right;
        }
    }
    return ret;
}

// 中序
#define MAX 100
int* preorderTraversal(struct TreeNode* root, int* returnSize){
    int* ret = (int*)malloc(sizeof(int) * MAX);
    struct TreeNode** stk = (struct TreeNode**)malloc(sizeof(struct TreeNode) * MAX);
    *returnSize = 0;
    int top = -1;
    struct TreeNode* p = root;
    while(p!=NULL || top>-1){
        if(p!=NULL){
            stk[++top]=p;//左节点入栈
            p=p->left;
        }
        else{
            ret[(*returnSize)++] = p->val;//返回左节点值
            p=stk[top--]->right;//转到右节点重复以上步骤
        }
    }
    return ret;
}
// 后序
int* postorderTraversal(struct TreeNode* root, int* returnSize){
    *returnSize=0;
    int* ans=(int*)malloc(sizeof(int)*100);
    struct TreeNode** stk=(struct TreeNode**)malloc(sizeof(struct TreeNode*)*100);
    int top=-1,i=0; //count记录访问右节点的个数
    struct TreeNode* pre=root;//p为遍历指针

    while(root!=NULL || top>-1){
        if(root!=NULL){
            stk[++top]=root;
            root=root->left;
        }
        else if(stk[top]->right!=NULL && stk[top]->right!=pre)
            root=stk[top]->right;
        else{
            pre=stk[top--];
            ans[i++]=pre->val;
            *returnSize=i;
        }
    }

    return ans;
}

二叉树遍历（层序）

/* 核心数据结构 */
struct TreeNode* queue[MAX]; // MAX代表树中节点范围
int front = 0;				 // 队头
int rear = 0; 				 // 队尾
struct TreeNode* cur;
queue[rear++] = root;		 // 根节点非空入队

while(front != rear) {
    int last = rear;		 // 每层结点的边界
    int colSize = 0;
    ret[*returnSize] = (int*)malloc(sizeof(int) * (last - front));
    while(front < last) {
        cur = queue[front++];
        ret[*returnSize][colSize++] = cur->val;
        if (cur->left) queue[rear++] = cur->left;
        if (cur->right) queue[rear++] = cur->right;
    }
}

九、图论

回溯 = 递归 + 剪枝

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }
    for (选择：本层集合中元素（树中节点***的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

// 链接：https://leetcode.cn/problems/all-paths-from-source-to-target/solution/by-carlsun-2-66pf/

深度优先搜索DFS

void dfs(参数) {
	if (终止条件) {
		存放结果；
		return;
	}
	
	for (选择：本节点所连接的其他节点) {
		处理节点；
		dfs(); // 递归
		回溯，撤销处理结果
	}
}

示例2

[1, 3] [3, 0, 1]中的1可能重复访问，图成环，无法到达n-1

visited数组标记防止成环

深搜三部曲：

1.确定递归函数，参数–可以在写递归函数的时候，发现需要什么参数，再去补充

void dfs(图，搜索到的节点)

2.确定终止条件–终止条件决定dfs是否死循环，栈溢出

if (终止条件) {

存放结果;

return;

}

如果一开始没有写终止条件，可能写在dfs递归逻辑里

3.处理目前搜索节点出发的路径

for循环去遍历目前搜索节点，所能到的所有节点

for (选择：本节点可以到达的其他节点) {

处理节点；

dfs(图，选择的节点); // 递归

回溯，撤销处理结果

}

如果需要回溯，可能使用栈来存储当前节点

十、优先队列

队列内部按照优先级排序，也叫堆排序，实现方式是二叉树

HW-CSTL库优先队列API

使用vos_priorityqueue

常用API

1.   VOS_PriQueCreate:创建一个priority queue，返回其控制块指针
   

•      参数：a)cmpFunc:比较函数;b)用户数据拷贝及释放对
  

2.   VOS_PriQuePush：插入一个数据到priority queue
   

•      参数：a)priority queue控制块;b)value
  

3.   VOS_PriQuePushBatch：插入一组数据到priority queue
   

•      参数：a)priority queue控制块b)beginItermAddr:用户数据的起始地址;c)待插入的数据个数；d)单个数据的大小
  

4.   VOS_PriQuePop：弹出头部数据
   

•      参数：a)priority queue控制块
  

5.   VOS_PriQueTop:返回堆顶数据
   

•      参数：a)priority queue控制块
  

6.   VOS_PriQueEmpty:判断priority queue是否为空
   

•      参数：a)priority queue控制块
  

7.   VOS_PriQueSize:获取priority queue中成员个数
   

•      参数：a)priority queue控制块
  

8.   VOS_PriQueDestory:删除priority queue所有成员及控制块
   

•      参数：a)priority queue控制块
  

十一、单调栈