python基础_看这一篇就够了

最新推荐文章于 2024-09-30 18:00:31 发布

原创最新推荐文章于 2024-09-30 18:00:31 发布 · 396 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#python #编程语言 #python基础 python培训

Python 同时被 2 个专栏收录

4 篇文章

订阅专栏

python 数据结构与算法分析

3 篇文章

订阅专栏

本文详细介绍了Python的基础知识，包括内建的原子和集合数据类型，如布尔、列表、字符串和集；控制结构如for、while和if语句；异常处理；函数定义；以及面向对象编程，特别是Fraction类的实现，包括构造方法、str方法、add方法和eq方法。通过实例展示了Python的数据操作和面向对象特性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Python是一门现代、易学、面向对象的编程语言。

1.数据

在 Python 以及其他所有面向对象编程语言中，**类都是对数据的构成（状态）以及数据能做什么（行为）的描述。**由于类的使用者只能看到数据项的状态和行为，因此类与抽象数据类型是相似的。**在面向对象编程范式中，数据项被称作对象。一个对象就是类的一个实例。 **

1.1 内建原子数据类型

// 整除
在这里插入图片描述

Python 通过 bool 类实现对表达真值非常有用的布尔数据类型。布尔对象可能的状态值是 True 或者 False，布尔运算符有 and、or 以及 not。
优先级从高到低 not and or
false or true =true
true or false = true
false or false = false

1.2 内建集合数据类型

列表

如果需要快速初始化列表，可以通过重复运算来实现，如下所示。

非常重要的一点是，重复运算返回的结果是序列中指向数据对象的引用的重复。下面的例子可以很好地说明这一点。

构建数据结构的方法
字符串
set
集（set）是由零个或多个不可修改的 Python数据对象组成的无序集合。集不允许重复元素，并且写成由花括号包含、以逗号分隔的一系列值。
字典
keys、values 和 items 方法均会返回包含相应值的对象。可以使用 list 函数将字典转换成列表。在表 1-8中可以看到， get 方法有两种版本。如果键没有出现在字典中，get 会返回 None。然而，第二个可选参数可以返回特定值。

2 输入与输出

在这里插入图片描述

3 控制结构

三大结构

for while 语句
if 语句
迭代

3.1 for while 语句

3.2 if 语句

Python也有单路分支结构，即 if 语句。如果条件为真，就会执行相应的代码。如果条件为假，**程序会跳过 if 语句，执行下面的语句。**例如，下面的代码段会首先检查变量 n 的值是否为负。如果值为负，那么就取它的绝对值，再计算它的平方根。
在这里插入图片描述

3.3 列表解析式

下面结构表示1到 10中奇数的平方数
在这里插入图片描述
任意支持迭代的序列都可用于列表解析式

4 异常处理

语法错误
SyntaxError : invalid syntax
语句不符合语法规范
eg:没有加‘ ：’ 括号类型使用错误
逻辑错误，通常，这些运行时错误被称为异常。
我们可以用try语句块调用print函数来处理这个异常。对应的except语句块捕捉到这个异常，并为用户打印一条提示信息。except会捕捉到 sqrt 抛出的异常并打印提示消息，然后会使用对应数字的绝对值来保证 sqrt 的参数非负。

程序员也可以使用 raise语句来触发运行时异常.

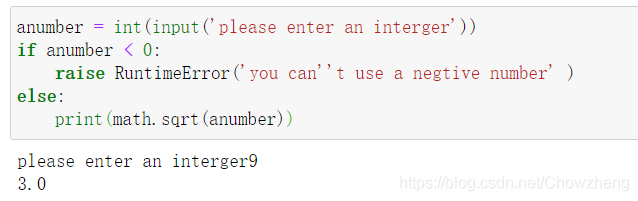
5 定义函数

以牛顿迭代法求平方根为例：
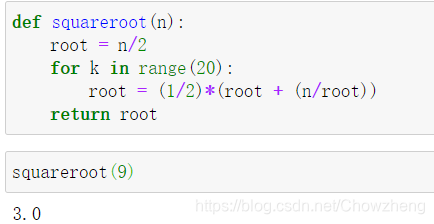
在这里插入图片描述

6 Python面向对象编程：定义类

6.1 Fraction 类

要展示如何实现用户定义的类，一个常用的例子是构建实现抽象数据类型 Fraction 的类。我们已经看到，Python提供了很多数值类。但是在有些时候，需要创建“看上去很像”分数的数据对象。
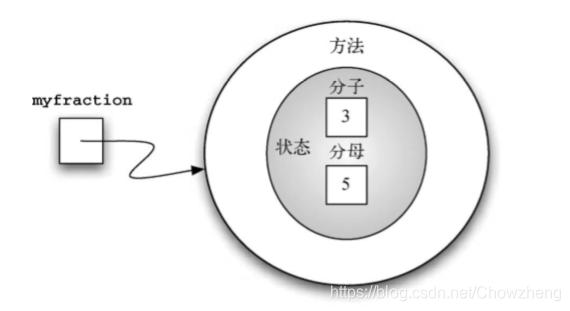
像3/5这样的分数由两部分组成。上面的值称作分子，可以是任意整数。下面的值称作分母，
可以是任意大于 0 的整数（负的分数带有负的分子）。尽管可以用浮点数来近似表示分数，但我们在此希望能精确表示分数的值。 Fraction 对象的表现应与其他数值类型一样。我们可以针对分数进行加、减、乘、除等运算，也能够使用标准的斜线形式来显示分数，比如 3/5。此外，所有的分数方法都应该返回结果的最简形式。这样一来，不论进行何种运算，最后的结果都是最简分数。

6.1.1 类及构建方法

6.1.1.1 Fraction类及其构造方法

在这里插入图片描述
self是一个总是指向对象本身的特殊参数，它必须是第一个形式参数。构造方法中的self.num定义了Fraction对象有一个叫做num的内部数据对象作为其状态的一部分。同理,self.den定义了分母。这两个实际参数的值在初始是赋予了状态，使得新创建的Fraction对象能够知道其初始值。

调用方法
myfunction = Fraction(3,5)
在这里插入图片描述

6.1.1.2 show 方法

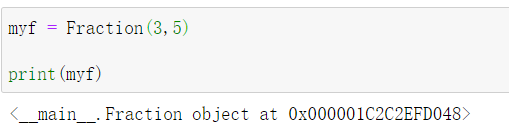
在这里插入图片描述
myf 唯一能做的就是显示存储在变量中的实际引用（地址本身）。
有两种办法可以解决这个问题。一种是定义一个 show 方法，使得 Fraction 对象能够将自己作为字符串来打印。不幸的是，这种方法并不通用。为了能正确打印，我们需要告诉 Fraction 类**如何将自己转换成字符串。**要完成任务，这是 print 函数所必需的。

方法1

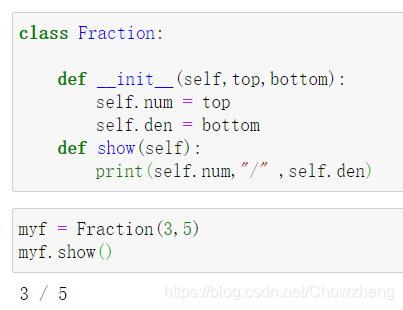
6.1.1.3 str 方法

之前默认实现是返回实例的地址字符串。
我们使用__str__返回字符串。
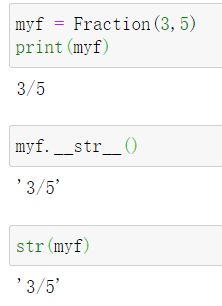
在这里插入图片描述

后两者是‘3/5’是因为返回了字符串myf

6.1.1.3 add 方法

在这里插入图片描述

虽然结果是对的，但不是最简分数，最好的表达是3/4
我们需要一种方法寻找分子和分母的最大公约数（greatest common divisor，GCD）。

6.1.1.4 eq 方法

如果我们要比较 f1 和 f2时，只有在它们是同一个对象的引用时，f1 == f2才为 True。这被称为浅相等.在当前实现中，分子和分母相同的两个不同的对象是不相等的。
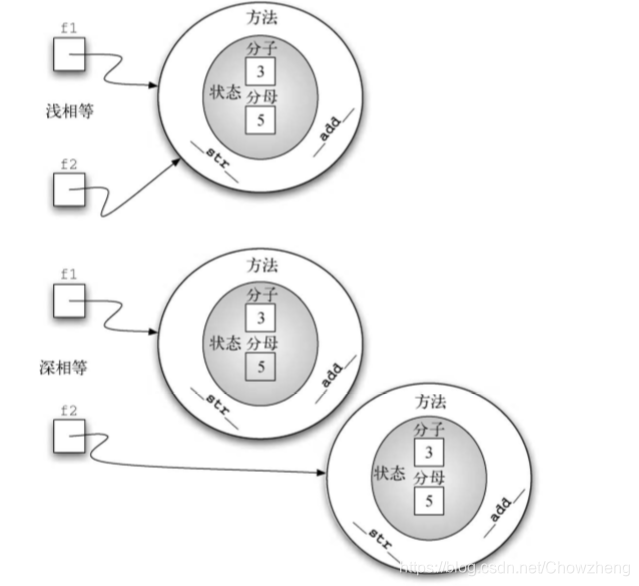
在这里插入图片描述
通过重写__eq__方法，可以建立深相等——根据值来判断相等，而不是根据引用

6.2 逻辑门与电路

最后一节介绍面向对象编程的另一个重要方面。继承使一个类与另一个类相关联，就像人们相互联系一样。与之类似，Python中的子类可以从父类继承特征数
据和行为。父类也称为超类。

class LogicGate:
    def __init__(self,n):
        self.label = n
        self.output = None
        
    def getLabel(self):
        return self.label
    def getOutput(self):
        self.output = self.performGateLogic()
        return self.output

class BinaryGate(LogicGate):
    def __init__(self, n):
        super().__init__(n)
        
        self.pinA = None
        self.pinB = None
    def getPinA(self):
        if self.pinA == None:
            return int(input('Enter pin A input for gata ' + \
                        self.getLabel() + '--->'))
        else:
            return self.pinA.getFrom().getOutput()
        
    def getPinB(self):
        return int(input('Enter pin B input for gata' + \
                        self.gatLabel() + '--->'))

class UnaryGata(LogicGate):
    def __init__(self,n):
        super().__init__(n)
        
        self.pin = None
        
    def getPin(self):
        return int(input('Enter Pin input for gata' + \
                        self.getLabel() +'--->'))
    
class AndGate(BinaryGate):
    def __init__(self,n):
        super().__init__(n)
    def performGateLogic(self):
        
        a = self.getPinA()
        b = self.getPinB()
        if a == 1 and b == 1:
            return 1
        else:
            return 0
class Connector:
    
    def __init__ (self,fgate,tagata):
        self.fromgate = fgate
        self.tofate = tgate
        
        tgate.setNextPin(self)
    def getFrom(self):
        return self.fromgate
    def getTo(self):
        return self.tofate

    def setNextPin(self,source):
        if self.pinA == None:
            self.pinA == source
        else:
            if self.pinB == None:
                self.pinB = source
            else:
                raise RuntimeError('Error : NO EMPTY PINS')