数据结构与算法之美【6】-栈

已于 2022-09-19 23:14:03 修改
阅读量650 收藏 1
点赞数
CC 4.0 BY-SA版权
分类专栏： 《数据结构与算法之美》读书笔记 文章标签： 数据结构 算法 栈 线性栈 链式栈
于 2021-03-13 00:14:12 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/Chiang2018/article/details/114713430
本文详细介绍了栈这一数据结构的基本概念，包括其操作特点、应用场景及其实现方式。具体讲解了函数调用栈、表达式求值及括号匹配中的栈应用，并提供了链式栈和线性栈的具体实现代码。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

目录

一、概述

二、栈的应用场景

1、函数调用栈

2、表达式中的栈

3、括号匹配中的栈

三、示例代码

1、链式栈

2、线性栈

一、概述

栈是一种操作受限的线性表，只允许从栈顶（栈顶指针）插入和删除数据，所以每次删除的元素都是最后进栈的元素，故栈也被称为后进先出（LIFO）表。栈主要包含两个操作，入栈（也叫做压栈）和出栈，即在栈顶插入数据和从栈顶删除数据。

栈既可以用数组来实现，也可以用链表来实现。用数组实现的栈，我们叫作顺序栈，用链表实现的栈，我们叫作链式栈。

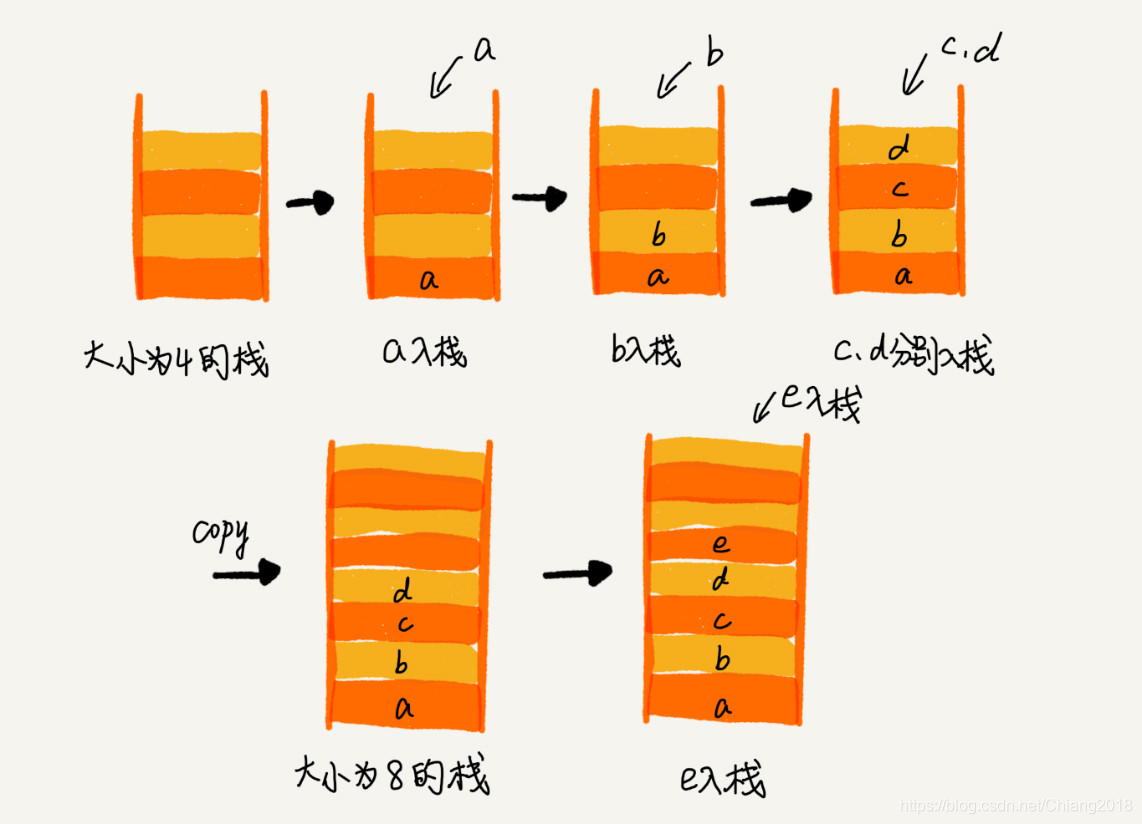
关于时间复杂度，因为在出栈只需要移动一个变量存储空间，所以它的时间复杂度为O(1)，但是对于入栈分两种情况：

1、栈空间固定不变

此时若空间不满，则直接入栈，若空间满，则丢弃不入栈，所以此时时间复杂度为O(1)

2、栈空间支持动态扩容

若此时栈未满时，时间复杂度不变，也为O(1)，但是当栈满时，需要重新分配内存，并复制栈内所有数据，此时：

  • 时间复杂度为：O(n)
  • 最好情况复杂度为：O(1)
  • 最坏情况复杂度为：O(n)
  • 均摊情况复杂度为O(1)

二、栈的应用场景

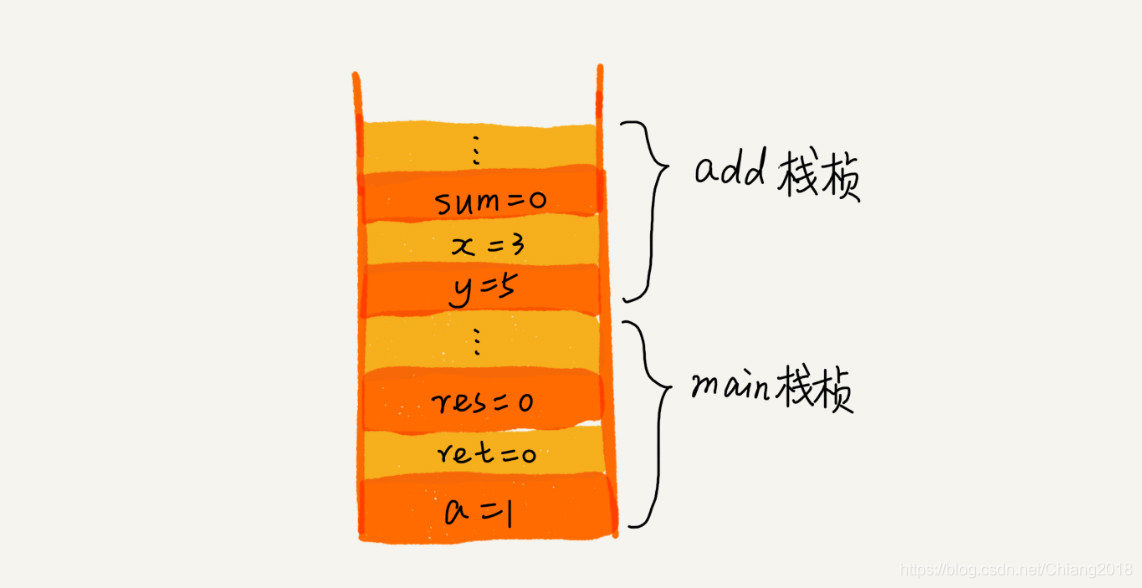
1、函数调用栈

我们知道，操作系统给每个线程分配了一块独立的内存空间，这块内存被组织成“栈”这种数据结构, 用来存储函数调用时的临时变量。即每进入一个函数，就会将临时变量作为一个栈帧入栈，当被调用函数执行完成返回时，将栈帧出栈。如下代码，在函数调用栈的顺序如下图所示：

int main() {
   int a = 1; 
   int ret = 0;
   int res = 0;
   ret = add(3, 5);
   res = a + ret;
   printf("%d", res);
   reuturn 0;
}

int add(int x, int y) {
   int sum = 0;
   sum = x + y;
   return sum;
}

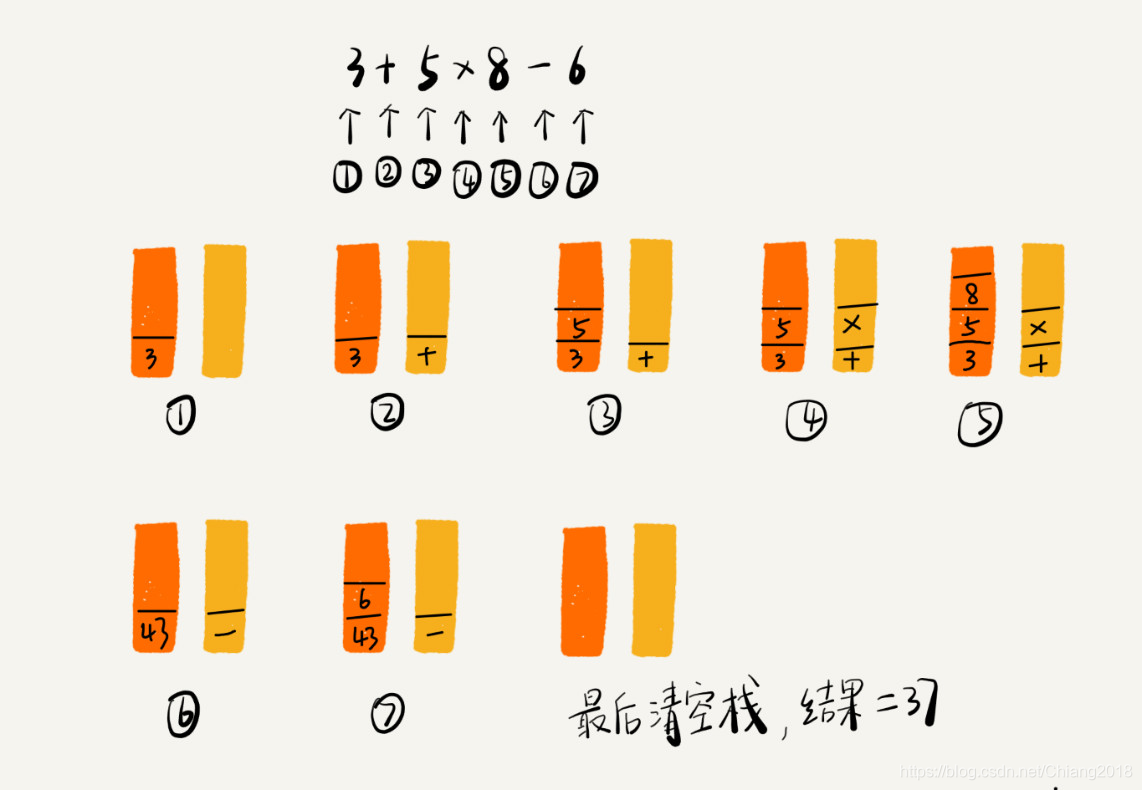
2、表达式中的栈

编译器如何利用栈来实现表达式求值？

实际上编译器是通过两个栈来实现的。其中一个保存操作数的栈，另一个是保存运算符的栈。编译器从左向右遍历表达式，当遇到数字，我们就直接压入操作数栈；当遇到运算符，就与运算符栈的栈顶元素进行比较，如果比运算符栈顶元素的优先级高，就将当前运算符压入栈；如果比运算符栈顶元素的优先级低或者相同，从运算符栈中取栈顶运算符，从操作数栈的栈顶取 2 个操作数，然后进行计算，再把计算完的结果压入操作数栈，继续比较。

我将 3+5*8-6 这个表达式的计算过程画成了一张图，你可以结合图来理解我刚讲的计算过程。

3、括号匹配中的栈

栈除了用栈来实现表达式求值，我们还可以借助栈来检查表达式中的括号是否匹配。

我们同样简化一下背景。我们假设表达式中只包含三种括号，圆括号 ()、方括号[]和花括号{}，并且它们可以任意嵌套。比如，{[] ()[{}]}或[{()}([])]等都为合法格式，而{[}()]或[({)]为不合法的格式。那我现在给你一个包含三种括号的表达式字符串，如何检查它是否合法呢？

这里也可以用栈来解决。我们用栈来保存未匹配的左括号，从左到右依次扫描字符串。当扫描到左括号时，则将其压入栈中；当扫描到右括号时，从栈顶取出一个左括号。如果能够匹配，比如“(”跟“)”匹配，“[”跟“]”匹配，“{”跟“}”匹配，则继续扫描剩下的字符串。如果扫描的过程中，遇到不能配对的右括号，或者栈中没有数据，则说明为非法格式。当所有的括号都扫描完成之后，如果栈为空，则说明字符串为合法格式；否则，说明有未匹配的左括号，为非法格式。

三、示例代码

1、链式栈

// 栈动态.cpp : 定义控制台应用程序的入口点。
//

// 单链表.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <stdlib.h>
#include <iostream>

template <class T>
class Node
{
public:
    T data;
    Node(T& item);
    Node<T>* next;
};

template<class T>
class LinkList
{
public:
    LinkList();
    ~LinkList();
    int getSize(void);
    bool IsEmpty(void);
    int gotoNext(void);
    int getPostion(void);
    int InsertNode(T& data);
    int DeleteNode(void);
    void getCurrNodeData(T& data);
    void setCurrNodeData(T& data);
    void clear();
    void print();

private:
    Node<T>* head;
    Node<T>* currNode;
    int size;
    int position;
    void freeNode(Node<T>* p);
};

/* 链表节点构造函数 */
template <class T>
Node<T>::Node(T& item)
{
    data = item;
    next = NULL;
}

/* 链表构造函数 */
template <class T>
LinkList<T>::LinkList()
{
    head = NULL;
    currNode = NULL;
    size = 0;
    position = -1;
}

/* 链表析构函数 */
template <class T>
LinkList<T>::~LinkList()
{
    clear();
}

/* 获取链表长度 */
template <class T>
int LinkList<T>::getSize(void)
{
    return size;
}

/* 判断链表是否为空 */
template <class T>
bool LinkList<T>::IsEmpty(void)
{
    return size==0?true:false;
}

/* 移动到下个节点，返回下个节点的位置值 */
template <class T>
int LinkList<T>::gotoNext(void)
{
    if(NULL == head)
    {
        return -1;
    }

    if(NULL == currNode)
    {
        return -1;
    }
    else
    {
        currNode = currNode->next;
        position++
    }

    return position;
}

/* 获取当前节点的位置 */
template <class T>
int LinkList<T>::getPostion(void)
{
    return position;
}

/* 在当前节点前插入新节点 */
template <class T>
int LinkList<T>::InsertNode(T& data)
{
    Node<T>* p = new Node<T>(data);

    if(0 == size)
    {
        head = p;
        head->next = NULL;
        currNode = p;
    }
    else
    {
        p->next = currNode->next;
        currNode->next = p;
        currNode = p;
    }

    size++;
    position++;
    return size;
}


/* 删除当前节点 */
template <class T>
int LinkList<T>::DeleteNode(void)
{
    if(0 == size)
    {
        return -1;
    }
    
    Node<T>* p = head;
    Node<T>* tmp;
    for(int i = 0;i < size;i++)
    {
        if(NULL == p)
        {
            return -1;
        }

        if(p->next == currNode)
        {
            p->next = currNode->next;
            break;
        }

        p = p->next;
    }

    tmp = currNode;

    if(currNode == head)
    {
        head = currNode->next;
    }

    if(NULL == currNode->next)
    {
        position--;
        currNode = p;
    }
    else
    {
        currNode = currNode->next;
    }
    

    freeNode(p);
    size--;
    if(0 == size)
    {
       position = -1;
    }

    return 0;
}

/* 释放指定节点的内存 */
template <class T>
void LinkList<T>::freeNode(Node<T>* p)
{
    if(!p)
    {
        delete p;
    }

    return;
}

/* 获取当前节点的数据 */
template <class T>
void LinkList<T>::getCurrNodeData(T& data)
{
    if(currNode)
    {
        data = currNode->data;
    }

    return ;
}

/* 修改当前节点的数据 */
template <class T>
void LinkList<T>::setCurrNodeData(T& data)
{
    if(currNode)
    {
        currNode->data = data;
    }

    return ;
}

/* 清空链表 */
template <class T>
void LinkList<T>::clear()
{
    if(0 == size)
    {
        return;
    }

    Node<T>* p = head;
    Node<T>* tmp = head->next;
    while(p)
    {
        freeNode(p);
        p = tmp;
        if(tmp)
        {
            tmp = tmp->next;
        }
    }

    head = NULL;
    currNode = NULL;
    size = 0;
    position = -1;

    return;
}

template <class T>
void LinkList<T>::print()
{
    if(0 == size)
    {
        return;
    }

    Node<T>* p = head;
    Node<T>* tmp = head->next;
    while(p)
    {
        std::cout<<p->data<<std::endl;
        p = tmp;
        if(tmp)
        {
            tmp = tmp->next;
        }
    }

    return;
}
template <class T>
class LinkedStack
{
private:
    LinkList<T>* link;
public:
    LinkedStack();
    void push(T& data);
    T pop();
    void ClearStack();
    int getSize();
    bool isEmpty();
};
template <class T>
LinkedStack<T>::LinkedStack()
{
    link = new LinkList<T>;
}
template <class T>
bool LinkedStack<T>::isEmpty()
{
    return link->IsEmpty();
}
template <class T>
int LinkedStack<T>::getSize()
{
    return link->size;
}

template <class T>
void LinkedStack<T>::ClearStack()
{
    link->clear();
}
template <class T>
void LinkedStack<T>::push(T& data)
{
    link->InsertNode(data);
}

template <class T>
T LinkedStack<T>::pop()
{
    T tmp;
    if(isEmpty())
    {
        return NULL;
    }
    
    link->getCurrNodeData(tmp);

    link->DeleteNode();

    return tmp; 
}

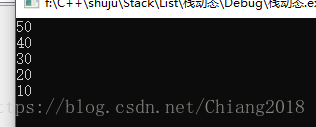
int main(int argc, _TCHAR* argv[])
{
    int j = 0;
    int a = 10,b=20,c=30,d=40,e=50;
    LinkedStack<int> list;

    list.push(a);
   
    list.push(b);
    list.push(c);
    list.push(d);
    list.push(e);

    j = list.pop();
    std::cout<<j<<std::endl;

    j = list.pop();
    std::cout<<j<<std::endl;

    j = list.pop();
    std::cout<<j<<std::endl;

    j = list.pop();
    std::cout<<j<<std::endl;

    j = list.pop();
    std::cout<<j<<std::endl;

    std::cin.get();
	return 0;
}

运行结果为：

这里写图片描述

2、线性栈

#include "stdafx.h"
#include <iostream>  
#include <new>  
   
//定义  
template<class T>  
class LineStack  
{  
public :  
    LineStack(int MaxListSize=10);  //构造函数
    ~LineStack()                             //析构函数 
    {
        delete[] elements;
    }  
  
    bool IsEmpty() const             //判断是否为空
    {
        return top==-1;
    }  

    bool IsFull() const               //判断是否满
    {
        return top==MaxSize-1;
    }  

    T pop(); //出栈 

    int push(const T& data);  //进栈

    T getPop();  //获取栈顶元素值

    void clear();  //清空栈

    void print() ;  
  
private:  
    int top;  //栈顶指针
    int MaxSize;  //数组最大长度
    T *elements;//一维动态数组  
  
};  

//实现...  
template<class T>  
LineStack<T>::LineStack(int MaxListSize)  
{   
    //基于公式的线性表的构造函数  
    MaxSize = MaxListSize;  
    elements = new T[MaxSize];  
    top = -1;  
}  
  
template<class T>  
T LineStack<T>::pop()  
{  
    if(IsEmpty()) 
    {
        return NULL;  
    }

    return elements[top--];  
}  
  
template<class T>  
int LineStack<T>::push(const T& data)  
{  
    if(IsFull())
    {
        return -1;
    }
    else
    {
        elements[++top] = data;
    }

    return 0;  
}  
  
  
template<class T>  
T LineStack<T>::getPop()  
{  
    if(IsEmpty()) 
    {
        return NULL;  
    }

    return elements[top]; 
}  
  
template<class T>  
void LineStack<T>::clear()  
{  
    top = -1;
    return true;  
}  
  
template<class T>  
void LineStack<T>::print()  
{  
    for(int i=0;i<=top;i++)
    {
        std:: cout<<elements[i]<<"   ";  
    }
}  
 
void LineStackSample()  
{  
    int j;
    int a = 10,b = 20,c = 30,d = 40;

    LineStack<int> S(10);  
    std::cout<<"IsFull  = "<<S.IsFull()<<std::endl;  
    std::cout<<"IsEmpty = "<<S.IsEmpty()<<std::endl;  
  
    S.push(a);
    S.push(b);
    S.push(c);
    S.push(d);

    j = S.pop();
    std::cout<<j<<std::endl;
    j = S.pop();
    std::cout<<j<<std::endl;
    j = S.pop();
    std::cout<<j<<std::endl;
    j = S.pop();
    std::cout<<j<<std::endl;

    return;
}  

int main(int argc, _TCHAR* argv[])  
{  
    LineStackSample();  
  
    //暂停操作  
    char str;  
    std::cin>>str;  
    //程序结束  
    return 0;  
}

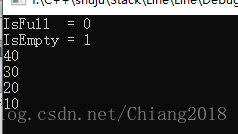
运行结果为：

这里写图片描述

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

Chiang木

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值