蓝桥之统计子矩阵

样例说明
满足条件的子矩阵一共有 19 , 包含:

大小为 1×1 的有 10 个。

大小为 1×2 的有 3 个。

大小为1×3 的有 2 个。

大小为 1×4 的有 1 个。

大小为 2×1 的有 3 个。

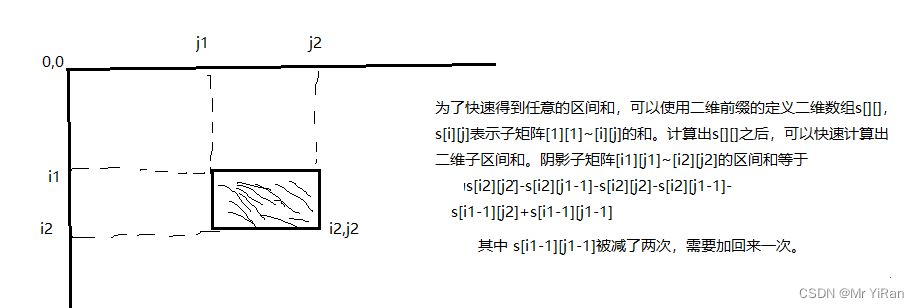
前缀和二维数组

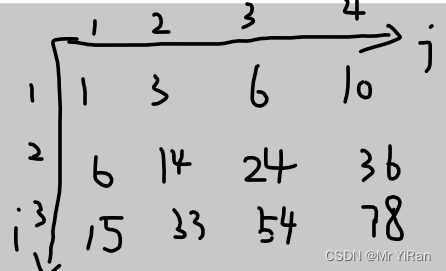
前缀和+暴力搜索

import java.util.*;
public class Main{

    private static int ans=0;

    public static void main(String[] args) {
      Scanner scanner=new Scanner(System.in);
      int N=scanner.nextInt();
      int M=scanner.nextInt();
      int K=scanner.nextInt();
      int[][] a=new int[N+1][M+1];
      int[][]  preSum = new int[N+1][M+1];
      for(int i=1;i<=N;i++){
          for(int j=1;j<=M;j++){
              a[i][j]=scanner.nextInt();
              //二维数组中的各个前缀合
              //
              preSum[i][j] = a[i][j]+preSum[i-1][j]+preSum[i][j-1]-preSum[i-1][j-1];
          }
      }
       //暴力枚举二维数组
        for(int i1=1;i1<=N;i1++){//遍历行
           for(int i2=i1;i2<=N;i2++){
               for(int j1=1;j1<=M;j1++){//遍历列
                   for(int j2=j1;j2<=M;j2++){
                      //枚举各个满足要求的前缀和
                       int z=preSum[i2][j2]-preSum[i2][j1-1]-preSum[i1-1][j2]+preSum[i1-1][j1-1];
                      // System.out.println(z);
                       if(z<=K){
                           ans++;
                       }
                   }
               }
           }
       }
        for (int i = 0; i <=N; i++) {
            for (int j = 0; j <=M; j++) {
                System.out.print(preSum[i][j]+"　");
            }
            System.out.println();
        }
        System.out.println(ans);
    }
}

4个for循环时间复杂度比较高
采用前缀和+滑动窗口
首先对每一列进行前缀和

  for(int i=1;i<=N;i++){
          for(int j=1;j<=M;j++){
              a[i][j]=scanner.nextInt();
              preSum[i][j] = a[i][j]+preSum[i-1][j];
          }
      }

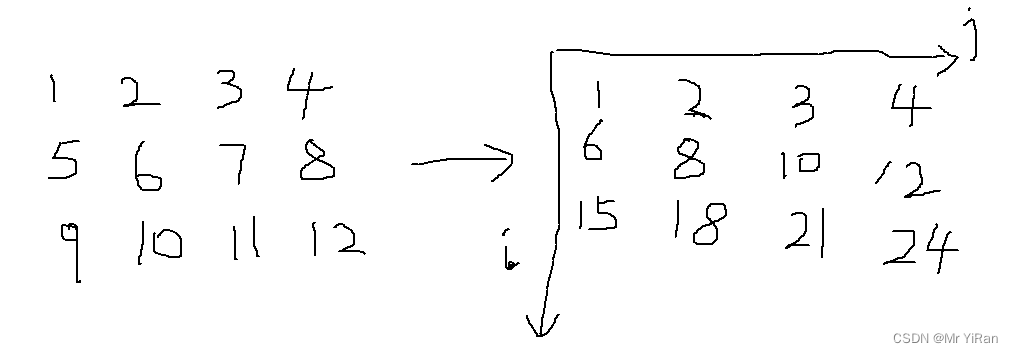
通过滑动窗口我们可以将4个for循环减少至3个。只需两层for循环遍历行，第三场for循环两个代表列的指针进行滑动窗口。
当遇到不满足条件的时候j+1向右移动列指针。

        for(int i1=1;i1<=N;i1++){
            for(int i2=i1;i2<=N;i2++){
                int sum=0;//一个范围的区间和结束需要重新将sum更新为0
                for(int j1=1,j2=1;j2<=M;j2++){
                    sum+=preSum[i2][j2]-preSum[i1-1][j2];//累加区间和
                    System.out.println(sum);
                    while(sum>K){
                        sum-=preSum[i2][j1]-preSum[i1-1][j1];//不符合条件，减去上一列的区间和(通过左边界的最上层的区间和减去左下边界下一层的区间和就等于上一列的区间和)
                        //System.out.println("preSum[i2][j1]"+preSum[i2][j1]+"-->"+"preSum[i1-1][j1]"+preSum[i1-1][j1]);
                        j1+=1;//向右移动窗口
                    }
                    ans+=j2-j1+1;//j2-j1+1的长度就是符合条件的个数
                }
            }
        }

完整代码：

import java.util.Scanner;
import java.io.*;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    private static StreamTokenizer re=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));//快速输入
    private static int nextInt() throws IOException {
        re.nextToken();
        return (int)re.nval;
    }
    public static void main(String[] args) throws IOException{
        //Scanner scan = new Scanner(System.in);
        //在此输入您的代码...

        int N=nextInt();
        int M=nextInt();
        int K=nextInt();
        int[][] a=new int[N+1][M+1];
        int[][]  preSum = new int[N+1][M+1];
        for(int i=1;i<=N;i++){
            for(int j=1;j<=M;j++){
                a[i][j]=nextInt();
                preSum[i][j] = a[i][j]+preSum[i-1][j];
            }
        }
        int ans=0;
        for(int i1=1;i1<=N;i1++){
            for(int i2=i1;i2<=N;i2++){
                int sum=0;//一个范围的区间和结束需要重新将sum更新为0
                for(int j1=1,j2=1;j2<=M;j2++){
                    sum+=preSum[i2][j2]-preSum[i1-1][j2];//累加区间和
                //    System.out.println(sum);
                    while(sum>K){
                        sum-=preSum[i2][j1]-preSum[i1-1][j1];//不符合条件，减去上一列的区间和(通过左边界的最上层的区间和减去左下边界下一层的区间和就等于上一列的区间和)
                        //System.out.println("preSum[i2][j1]"+preSum[i2][j1]+"-->"+"preSum[i1-1][j1]"+preSum[i1-1][j1]);
                        j1+=1;//向右移动窗口
                    }
                    ans+=j2-j1+1;//j2-j1+1的长度就是符合条件的个数
                }
            }
        }
        System.out.println(ans);
    }
}

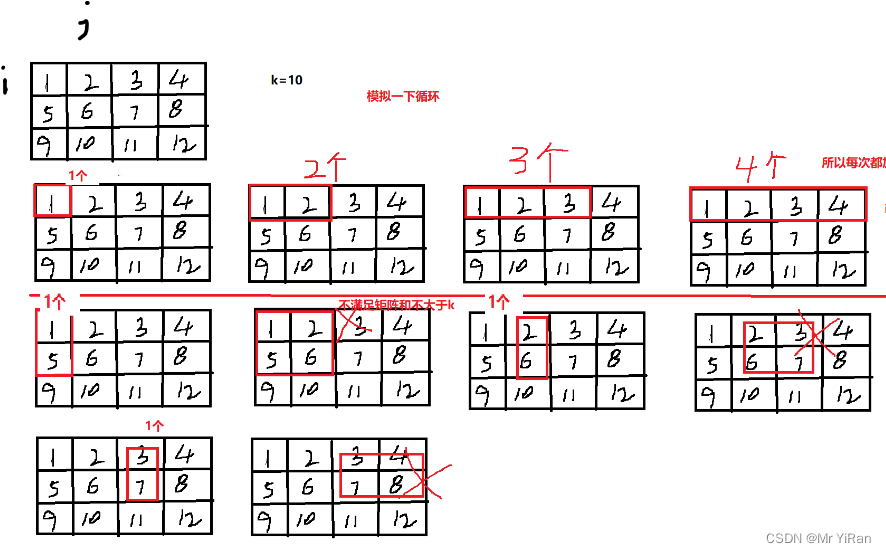
模拟过程