目录
非参数模型:k-最近邻,决策树和随机森林。介绍交叉验证,超参数调整和集合模型。
非参数学习者。
事情即将变得有点......摇摆不定。
与我们迄今为止所涵盖的方法相比 - 线性回归,逻辑回归和SVM,其中模型的形式是预定义的 - 非参数学习者没有先验地指定的模型结构。我们没有推测在训练模型之前我们试图学习的函数f的形式,正如我们之前使用线性回归所做的那样。相反,模型结构纯粹是根据数据确定的。
这些模型对训练数据的形状更加灵活,但这有时会以可解释性为代价。这很快就会更有意义。我们跳吧。
k-最近邻居(k-NN)
“你是你最亲密的朋友的平均水平。”
k-NN似乎太简单了,不能成为机器学习算法。想法是通过找到k个最近数据点标签的平均值(或模式)来标记测试数据点x。
看看下面的图片。假设您想知道神秘绿色圆圈是红色三角形还是蓝色方形。你是做什么?
您可以尝试提出一个花哨的方程式,该方程式查看Green Circle位于下方坐标平面上的位置并进行相应的预测。或者,你可以看看它最近的三个邻居,并猜测绿圈可能是红三角。你还可以进一步扩展圆圈并查看五个最近的邻居,然后进行预测(其五个最近邻居中的3/5是蓝色方块,所以当k =时我们猜测神秘绿色圆圈是蓝色方块5)。
k-NN插图,k = 1,3和5.要对上面的神秘绿色圆圈(x)进行分类,请查看其单个最近邻居“红色三角形”。所以,我们猜测 ŷ =“红三角”。当k = 3时,看看3个最近的邻居:这些模式再次是“红三角”,所以ŷ =“红三角”。在k = 5的情况下,我们采用5个最近邻居的模式。现在,请注意 ŷ变成“蓝色方块”。来自维基百科的图片。
而已。这是k-最近邻居。如果变量是连续的(如房价),或者如果它们是分类的(如猫与狗),你可以查看k个最接近的数据点并取其值的平均值。
如果你想猜测未知的房价,你可以拿一些地理位置相近的房子的平均值,你最终会得到一些非常好的猜测。这些甚至可能优于某些经济学家建立的参数回归模型,该模型估算了床/浴室,附近学校,公共交通距离等的模型系数。
如何使用k-NN预测房价:
1)存储训练数据,诸如邮政编码,邻居,卧室数,平方英尺,距公共交通工具的距离等特征的矩阵X,以及相应销售价格的矩阵Y.
2) 根据X中的特征,根据与相关房屋的相似性对训练数据集中的房屋进行排序。我们将在下面定义“相似度”。
3)取最近k个房屋的平均值。这是你对销售价格的猜测(即y)
k-NN不需要将Y与X相关联的预定义参数函数f(X)的事实使得它非常适合于关系太复杂而无法用简单线性模型表达的情况。
距离指标:定义和计算“接近度”
当您找到“最近邻居”时,如何计算距离相关数据点的距离?你如何在数学上确定上面例子中哪个蓝色方块和红色三角形最接近绿色圆圈,特别是如果你不能只绘制一个漂亮的2D图形和眼球呢?
最直接的衡量标准是欧几里德距离(直线,“随着乌鸦飞行”)。另一个是曼哈顿距离,就像步行街区。例如,您可以想象曼哈顿距离在涉及优步驾驶员票价计算的模型中更有用。
绿线=欧几里德距离。蓝线=曼哈顿距离。资料来源:维基百科
还记得毕达哥拉斯定理找到直角三角形的斜边长度吗?
![]()
c =斜边的长度(上面的绿线)。a和b =其他边的长度,成直角(上面的红线)。
根据c求解,我们通过取a和b的平方长度之和的平方根来找到斜边的长度,其中a和b是三角形的正交边(即它们与之成90度角)彼此,在空间中垂直方向)。
![]()
发现在两个正交方向给定的载体中的斜边的长度的这样的想法推广到许多方面,这是我们如何推导欧几里德距离的公式d(P,Q)点之间的p和q在Ñ维空间:

欧几里德距离的公式,来自毕达哥拉斯定理。
使用此公式,您可以计算所有训练数据点与您尝试标记的数据点的接近程度,并采用k个最近邻居的均值/模式进行预测。
通常情况下,您不需要手动计算任何距离指标 - 快速Google搜索会显示NumPy或SciPy中预先构建的功能,这些功能将为您完成此操作,例如euclidean_dist = numpy.linalg.norm(p-q)- 但看到八年级的几何概念最终会如何变得有趣有助于今天建立ML模型!
选择k:使用交叉验证调整超参数
要决定使用哪个k值,您可以使用不同的k值和交叉验证来测试不同的k-NN模型:
- 将您的训练数据分成几个部分,并在除一个部分之外的所有部分训练您的模型; 使用保持段作为“测试”数据。
- 通过将模型的预测(ŷ)与测试数据的实际值(y)进行比较,了解模型的执行情况。
- 选择平均而言,在所有迭代中产生最低误差的平均值。
交叉验证说明。分裂和迭代的数量可以变化。
较高的k可防止过度拟合
值越高ķ帮助解决过学习,但如果价值ķ太高模型将是非常偏颇和不灵活。举个极端的例子:如果k = N(数据点的总数),模型就会将所有测试数据笨拙地分类为训练数据的均值或模式。
如果动物数据集中最常见 的动物是苏格兰折叠小猫,那么将k设置为N(训练观察数量)的k-NN 将预测世界上的其他动物也是苏格兰折叠小猫。在维沙尔看来,这将是非常棒的。Samer不同意。

完全无偿的苏格兰折叠.gif。我们称之为学习假期。?
在现实世界中何处使用k-NN
您可以使用k-NN的一些示例:
- 分类:欺诈检测。由于您只是存储更多数据点,因此可以使用新的培训示例立即更新模型,从而可以快速适应新的欺诈方法。
- 回归:预测房价。在住房价格预测中,字面意义上的“近邻”实际上是价格相似的良好指标。k-NN在物理接近度很重要的领域很有用。
- 输入缺失的训练数据。如果.csv中的某列有大量缺失值,则可以通过采用均值或模式来估算数据。k-NN可以让您对每个缺失值进行更准确的猜测。
决策树,随机森林
制作一个好的决策树就像玩一个“20个问题”的游戏。
右边的决策树描述了泰坦尼克号上的生存模式。
第一个分裂的根源决策树应该是这样,你应该问的20个问题,第一个问题:你希望将数据尽可能干净分离,从而最大限度地提高信息增益从分裂。
如果你的朋友说“我正在考虑一个名词,请问我最多20个是/否的问题来猜测它是什么”,你的第一个问题是“它是土豆吗?”,那么你就是一个笨蛋,因为他们我会说不,你几乎没有获得任何信息。除非你碰巧知道你的朋友一直在想土豆,或者正在考虑一下。然后你做得很好。
相反,像“这是一个对象吗?”这样的问题可能更有意义。
这有点像医院如何对患者进行分类或接近鉴别诊断。他们提前问几个问题并检查一些基本的生命体征,以确定你是否会立即死亡或什么的。他们不会在你走进门时进行活组织检查以检查是否患有胰腺癌。
有一些方法可以量化信息增益,这样您就可以基本上评估每个可能的训练数据分割,并最大限度地提高每个分组的信息增益。这样,您可以尽可能有效地预测每个标签或值。
现在,让我们看一下特定的数据集,并谈谈我们如何选择拆分。
泰坦尼克号数据集
Kaggle有一个Titanic 数据集,用于很多机器学习的介绍。当泰坦尼克号沉没时,2,224名乘客和机组人员中有1,502人遇难。尽管有一些运气,但女性,儿童和上层阶级更有可能生存。如果你回顾上面的决策树,你会发现它在某种程度上反映了性别,年龄和阶级的变化。
在决策树中选择拆分
熵是一组中的紊乱量(通过基尼指数或交叉熵测量)。如果值真的是混合的,那就有很多熵; 如果你可以干净地分割价值,就没有熵。对于父节点上的每个拆分,您希望子节点尽可能纯净 - 最小化熵。例如,在泰坦尼克号中,性别是生存的一个重要决定因素,因此在第一次拆分中使用此功能是有意义的,因为它是导致信息获取最多的那个。
让我们来看看我们的泰坦尼克号变量:

资料来源:Kaggle
我们通过选择其中一个变量并根据它来分割数据集来构建树。
第一次拆分将我们的数据集分为男性和女性。然后,女性分支在年龄上再次分裂(最小化熵的分裂)。同样,男子分会按阶级分开。通过跟随新乘客的树,您可以使用树来猜测它们是否已经死亡。
泰坦尼克号的例子是解决分类问题(“生存”或“死亡”)。如果我们使用决策树进行回归 - 比如预测住房价格 - 我们会对确定住房价格的最重要特征进行分割。多少平方英尺:大于或小于___?多少间卧室和浴室:多于或少于___?
然后,在测试期间,您将通过所有拆分运行特定房屋,并将房屋最终的最终叶节点(最底部节点)中的所有房屋价格的平均值作为您对销售价格的预测。
您可以使用决策树模型调整一些超参数,包括max_depth和max_leaf_nodes。请参阅决策树上的scikit-learn模块,以获取有关定义这些参数的建议。
决策树是有效的,因为它们易于阅读,即使数据混乱也很强大,并且在训练后一次性部署便宜。决策树也适用于处理混合数据(数字或分类)。
也就是说,决策树在训练时计算成本高,具有过度拟合的巨大风险,并且倾向于找到局部最优,因为它们在分裂之后无法返回。为了解决这些弱点,我们转向一种方法,说明将许多决策树组合成一个模型的能力。
随机森林:决策树的集合
由许多模型组成的模型称为集合模型,这通常是一种成功的策略。
单个决策树可以进行大量错误的调用,因为它具有非常黑白的判断。一个随机森林是元估计是将许多决策树,与一些有用的修改:
- 可以在每个节点上拆分的功能数量限制为总数的一定百分比(这是您可以选择的超参数 - 有关详细信息,请参阅scikit-learn文档)。这确保了集合模型不会过分依赖任何单个特征,并且可以合理地使用所有潜在的预测特征。
- 每个树在生成其分割时从原始数据集中绘制随机样本,添加另一个随机性元素以防止过度拟合。
这些修改还可以防止树木过于高度相关。如果没有上面的#1和#2,每个树都是相同的,因为递归二进制分裂是确定性的。
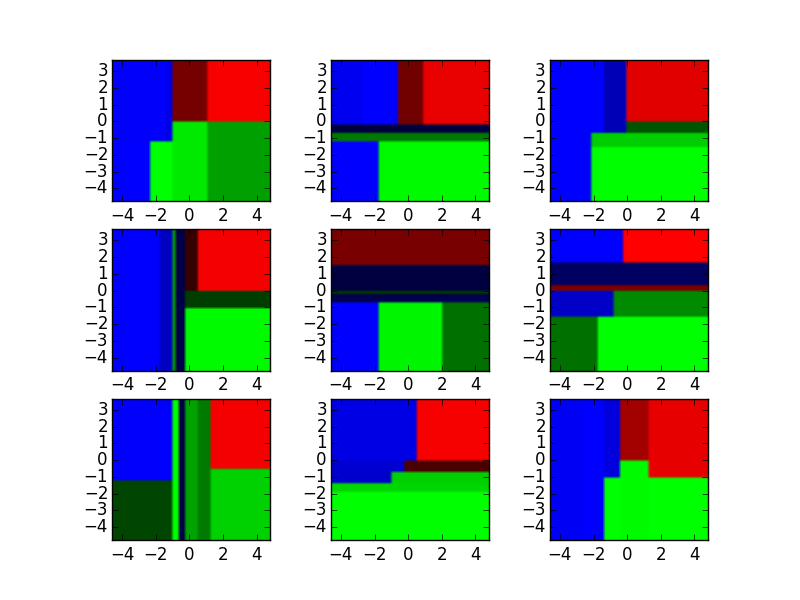
为了说明,请参阅下面的这九个决策树分类器。
资料来源:http://xenon.stanford.edu/~jianzh/ml/
这些决策树分类器可以聚合成一个随机森林集合,它组合了它们的输入。将每个决策树输出的水平轴和垂直轴视为特征x1和x2。在每个特征的某些值处,决策树输出“蓝色”,“绿色”,“红色”等的分类。
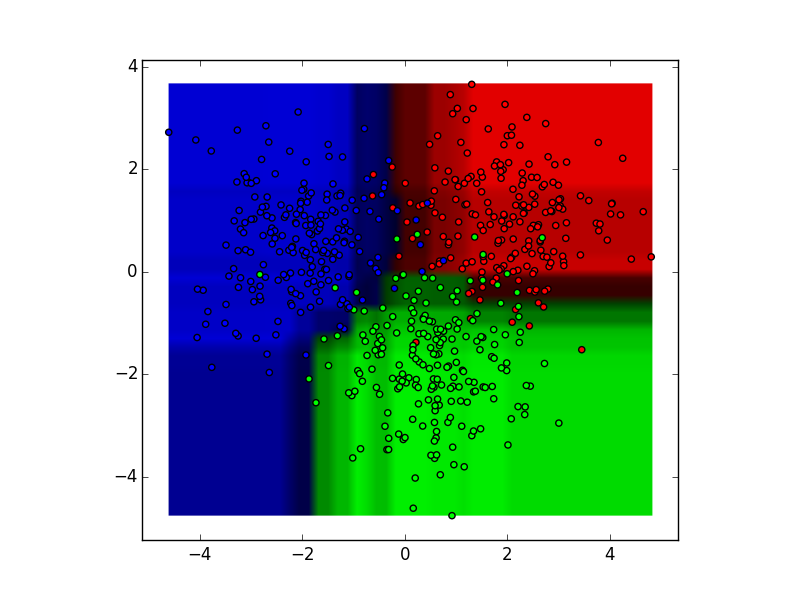
资料来源:http://xenon.stanford.edu/~jianzh/ml/
这些结果通过模态投票或平均聚合成单个集合模型,最终胜过任何单个决策树的输出。
随机森林是建模过程的一个很好的起点,因为它们往往具有强大的性能,对较少清理的数据具有高容忍度,并且可用于确定哪些特征在许多特征中实际上重要。
还有许多其他聪明的集合模型结合了决策树并产生了出色的性能 - 以XGBoost(极限梯度提升)为例。
有了这个,我们总结了我们对有监督学习的研究!
干得好。在本节中,我们介绍了:
- 两种非参数监督学习算法:k-NN和决策树
- 措施距离和信息增益
- 随机森林,是集合模型的一个例子
- 交叉验证和超参数调整
希望您现在对我们如何在给定训练数据集的情况下学习f有一些坚实的直觉,并使用它来对测试数据进行预测。
接下来,我们将讨论如何在第3部分:无监督学习中解决我们没有任何标记的训练数据的问题。
练习材料和进一步阅读
2.3a - 实施k-NN
尝试本演练,从头开始在Python中实现k-NN。您可能还想查看scikit-learn文档,以了解预构建实现的工作原理。
2.3b - 决策树
尝试“ 统计学习简介”第8章中的决策树实验室。您还可以使用Titanic数据集,并查看本教程,其中包含与上述相同的概念及附带的代码。以下是随机森林的scikit-learn实现,用于数据集的开箱即用。
原文:https://medium.com/machine-learning-for-humans/supervised-learning-3-b1551b9c4930
 非参数学习与集合模型
非参数学习与集合模型







 本文探讨了非参数监督学习算法k-NN和决策树,介绍了距离度量、信息增益概念,以及随机森林集合模型的原理。通过泰坦尼克号数据集实例,展示了决策树的构建与拆分选择。
本文探讨了非参数监督学习算法k-NN和决策树,介绍了距离度量、信息增益概念,以及随机森林集合模型的原理。通过泰坦尼克号数据集实例,展示了决策树的构建与拆分选择。






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








