LeetCode：最大网络秩

解决方案的性能：

时间复杂度：O（n^2）

题目描述：

n 座城市和一些连接这些城市的道路 roads 共同组成一个基础设施网络。每个 roads[i] = [a_i, b_i] 都表示在城市 a_i 和 b_i 之间有一条双向道路。

两座不同城市构成的城市对的网络秩定义为：

与这两座城市直接相连的道路总数。如果存在一条道路直接连接这两座城市，则这条道路只计算一次 。整个基础设施网络的最大网络秩是所有不同城市对中的最大网络秩 。

给你整数 n 和数组 roads，返回整个基础设施网络的最大网络秩 。

示例 1：

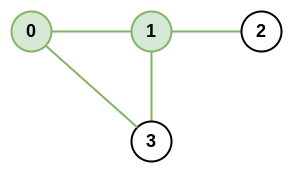
输入：n = 4, roads = [[0,1],[0,3],[1,2],[1,3]]

输出：4

解释：城市 0 和 1 的网络秩是 4，因为共有 4 条道路与城市 0 或 1 相连。位于 0 和 1 之间的道路只计算一次。

示例 2：

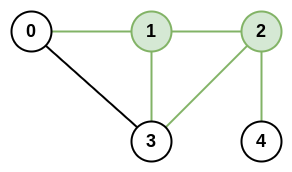
输入：n = 5, roads = [[0,1],[0,3],[1,2],[1,3],[2,3],[2,4]]

输出：5

解释：共有 5 条道路与城市 1 或 2 相连。

提示：

2 <= n <= 100

0 <= roads.length <= n * (n - 1) / 2

roads[i].length == 2

0 <= a_i, b_i <= n-1

a_i != b_i

解题思路：

通过题干很容易想到的要找出度最大的节点和度次大的节点，但容易忽略的是度最/次大的节点可能不止一个，而是一组！

首先建立邻接矩阵以标记节点之间是否连通，并创建一个单独的数组记录各节点的度。

之后如果最大度值节点只有一个，就看次大度值节点里有没有不与之不相连的；假使存在，那结果为first + second，否则结果为first + second - 1；

如果度最大度值节点为一组，则查找该组节点里是否有不相连的节点；如果存在，结果为first * 2，否则结果为first * 2 - 1；

代码：

class Solution {
public:
    int maximalNetworkRank(int n, vector<vector<int>>& roads) {
        vector<vector<bool>> con(n,vector<bool>(n,false));
        vector<int> degree(n,0);
        //在邻接矩阵上标记节点连接情况，并统计出各节点的度
        for(auto road : roads){
            int x = road[0],y = road[1];
            con[x][y] = true;
            con[y][x] = true;
            degree[x]++;
            degree[y]++;
        }

        int fir = 0,sec;
        vector<int> firArr,secArr;
        //遍历度统计数组，找出其中的最大值和次大值，以及其对应的节点
        for(int i = 0;i < n;i++){
            if(degree[i] > fir){
                sec = fir;
                secArr = firArr;

                fir = degree[i];
                firArr.clear();
                firArr.emplace_back(i);
            }
            else if(degree[i] == fir)
            firArr.emplace_back(i);
            else if(degree[i] > sec){//此处是为应对出现倒阶梯型增长的数组
                sec = degree[i];
                secArr.clear();
                secArr.emplace_back(i);
            }
            else if(degree[i] == sec)
            secArr.emplace_back(i);
        }
        //最大度值节点只有一个，查看次大度值节点里有没有不与之相连的；假使存在，结果为first + second，否则结果为first + second - 1
        if(firArr.size() == 1){
            for(auto v : secArr){
                if(!con[firArr[0]][v])  return fir + sec;
            }
            return fir + sec - 1;
        }
        //最大度值节点为一组，查找该组节点里是否有不相连的节点；如果存在，结果为first * 2，否则结果为first * 2 - 1；
        for(auto u : firArr){
            for(auto v : firArr){
                if(u != v&&!con[u][v]) return fir * 2;
            }
        }
        return fir * 2 - 1;
    }
};