解题报告（3）数组

第一种：for循环遍历

第二种：

 

 

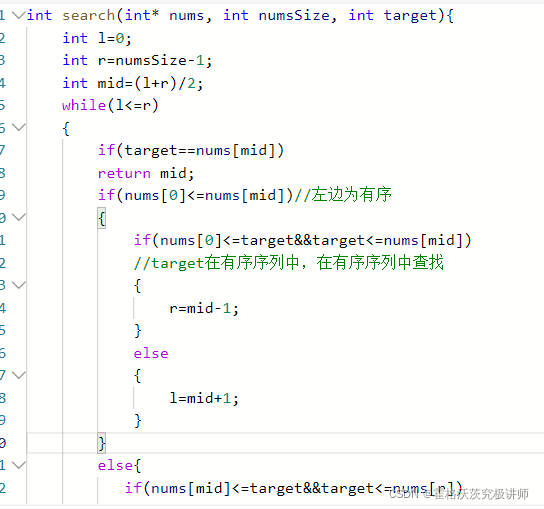
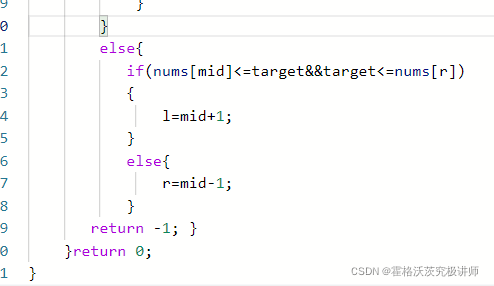
利用二分查找思想

步骤

（1）：定义左边界，右边界，中点mid

（2）：由于数组经过旋转，被分为两个有序序列，而以mid为界，其左右必有一个有序序列

所以先以（nums【0】<mid）为判断条件，判断哪个是有序序列

（3）：判断target是否在有序序列中

附二分查找模板

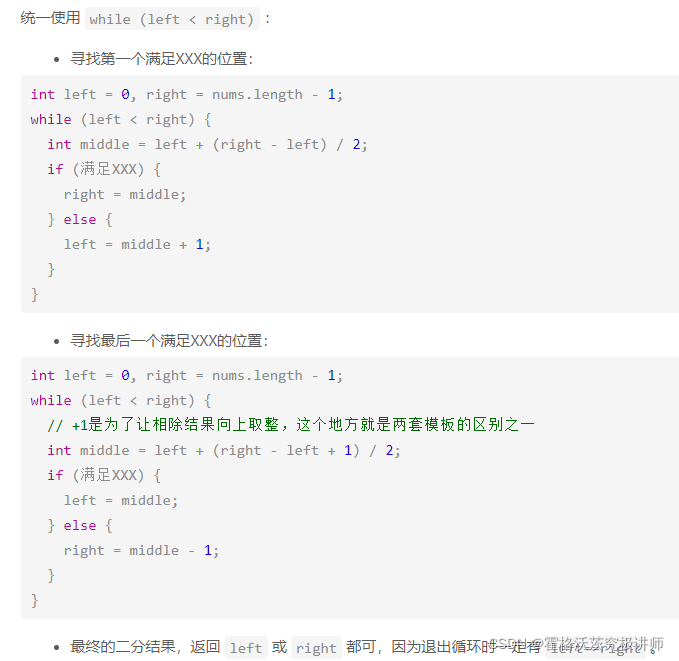
 第二题：数组仍升序，但可能存在相同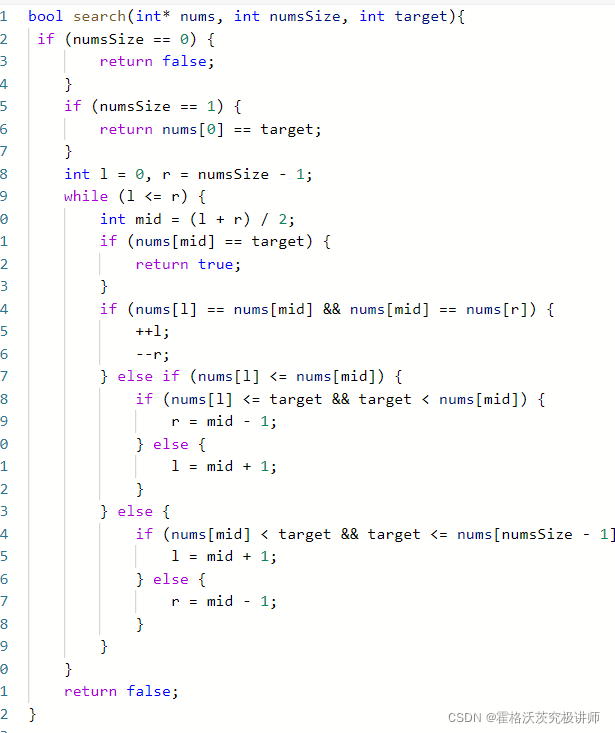数字

 添加特殊情况左界和右界和中点都相等

即将左右边界都+1（一定不是target）

第三题

 

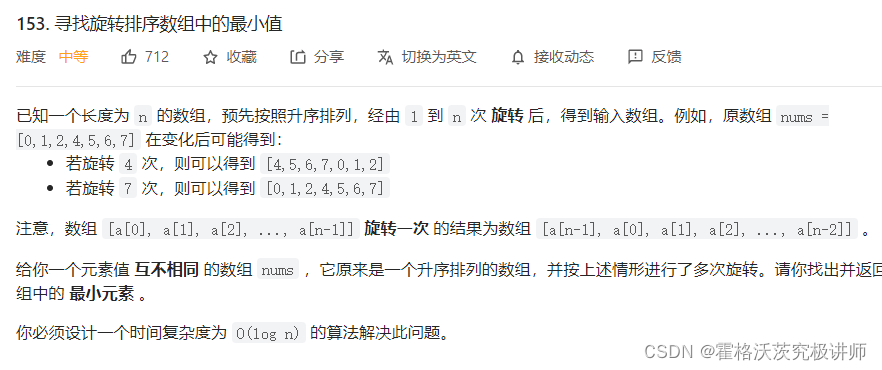
直接ctrl+v复制过来的。。

虽然与二分查找相类似，但有点不同

考虑旋转后数组最后元素x，最小值左边元素必大于x，最小值右边元素必小于x，（因为最小值一定是翻转后的第一个数）

X可类推至high（第一次的high就是x，第二次时high要么仍然是X，要么high到X已经被抛弃）

所以当num[mid]<num[high]时，说明mid在最小值右边，所以抛弃mid到high的一段，即high=pivot

第四五题 斐波那契数列

 第六题

 第二种方法：动态规划  即循环数组

需考虑动态转移方程：T（n+3）=...

边界条件：T0 T1 T2

构造循环数组

 

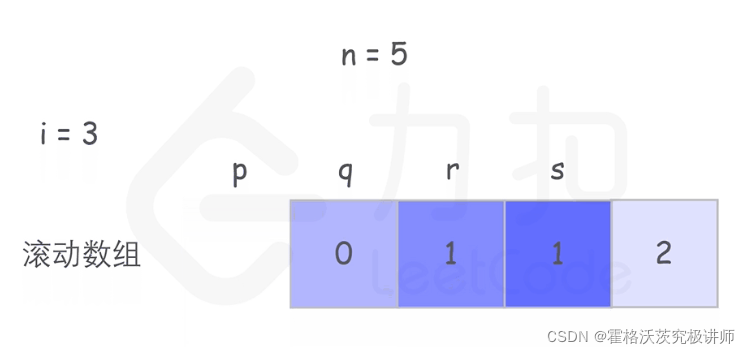
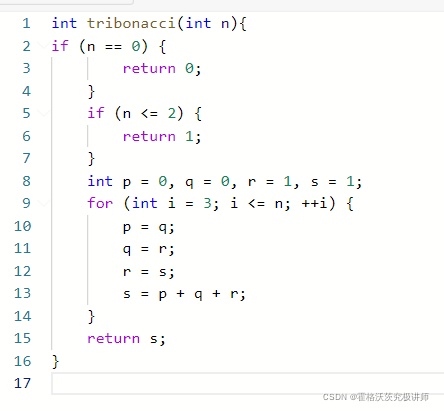
 i=3时赋值，循环1次

循环赋值，最后输出s

小结：学了二分查找和动态规划（也可以说是从答案上看了）