代码随想录算法训练营第十二天 | 239. 滑动窗口最大值、347.前 K 个高频元素

239. 滑动窗口最大值

题目链接：Leetcode239. 滑动窗口最大值

文章讲解：代码随想录—239. 滑动窗口最大值

思路：
一开始的思路就是暴力解法，外层循环里面套一个小循环，时间复杂度不可能只是线性。

本题和209. 长度最小的子数组区别在于，本题需要输出某一个数组元素，而209题只需要输出符合条件的数组长度即可，因此不能用简单的滑动窗口解决问题。

大顶堆每次只能弹出最大值，因此也无法用大顶堆解决问题。

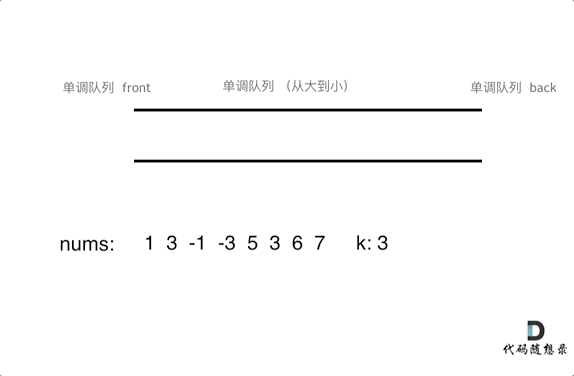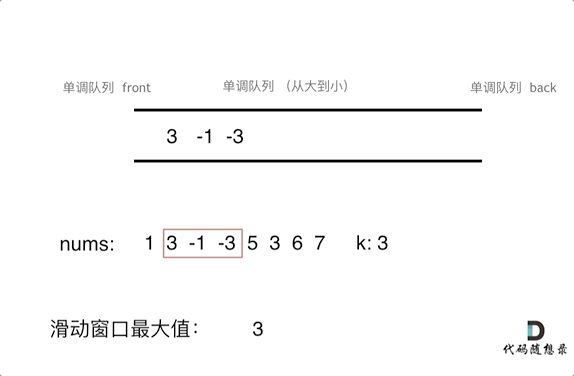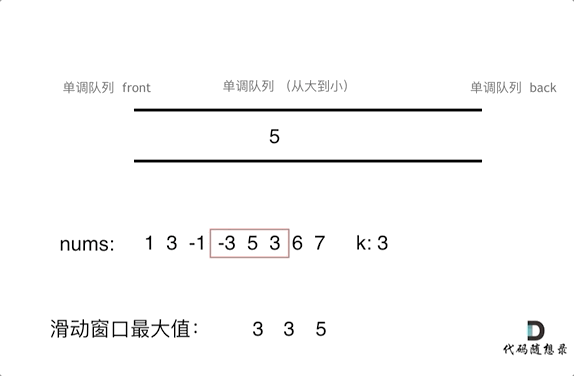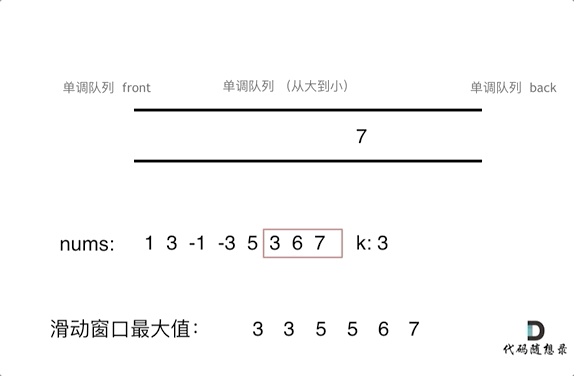
本题是用单调队列解决的，单调队列维护的不是队列中的所有元素，只需要维护有可能成为最大值的几个元素即可，如下图。否则如果完全按着从大到小或者从小到大的顺序成为优先队列，就没有办法随着窗口移动继续维护了。

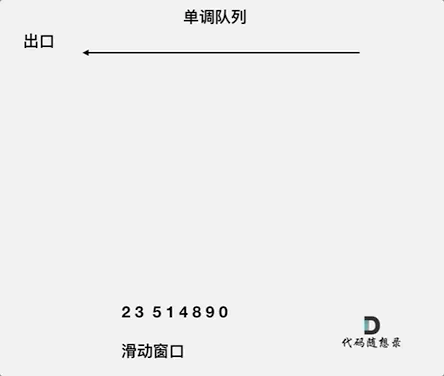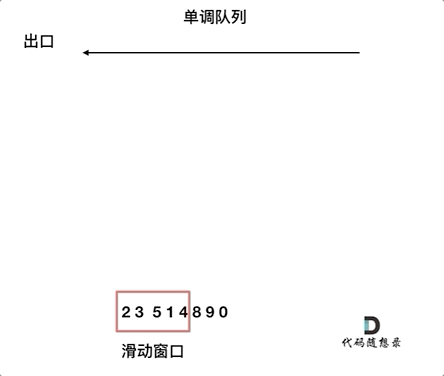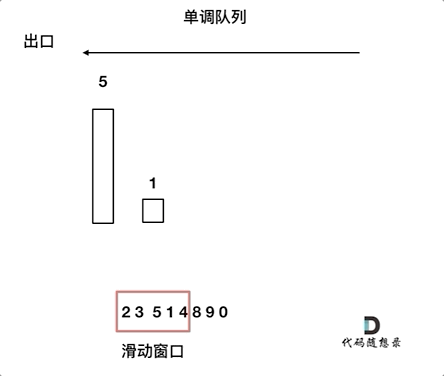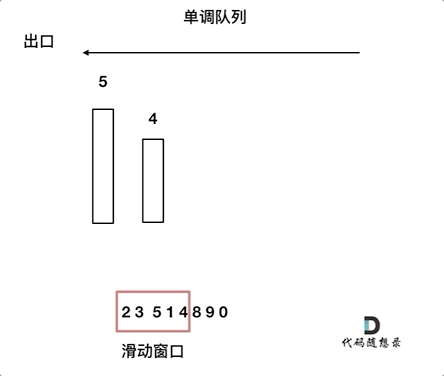
随着窗口滑动，只需要维护当前窗口最大值及之后的窗口元素。当下一个弹出值是当前最大值时，只需要把当前最大值从队列中弹出即可，队列中下一个元素成为当前最大值。录入下一个元素时，要比较队尾元素是否比新录入值大，如果队尾元素小，就要把队尾元素弹出，然后继续比较队尾元素，直到录入元素小，把它插入到队列尾部。综上，本题需要自己维护队列。

class Solution {
private:
    class MyQueue {
    public:
        deque<int> que;

        void push(int value) {
            while (!que.empty() && value > que.back()) que.pop_back();
            que.push_back(value);
        }

        void pop(int value) {
            if (!que.empty() && value == que.front()) que.pop_front();
        }

        int front() {
            return que.front();
        }
    };
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        MyQueue que;
        vector<int> res;
        for (int i = 0; i < k; i ++) {
            que.push(nums[i]);
        }
        res.push_back(que.front());
        for (int i = k; i < nums.size(); i ++) {
            que.pop(nums[i - k]);
            que.push(nums[i]);
            res.push_back(que.front());
        }
        return res;
    }
};

时间复杂度：O(n)

空间复杂度：O(k) 

347. 前K个高频元素

题目链接：Leetcode347. 前K个高频元素

文章讲解：代码随想录—347. 前K个高频元素

思路：

因为之前做过散列表的题，因此能首先想到用 map 统计各个元素出现的频率。但更重要的是后续根据频率的排序方法。

乍一看题，要找频率最高的k个元素，会想用大根堆。但是因为我们只维护大小为k的队列，后续再更新队列时，弹出的是大根堆的顶部，也就是当前队列频率最高的元素，这显然不是我们想要的，因此这道题中选用的是小根堆。

需要注意的是，虽然是小根堆，但建立的时候写的却是 left > right，大根堆则是 right < left。

此外，因为是小根堆，转到答案数组时需要从后往前记录，因此设置答案数组 vector 的时候要规定数组大小 k。

class Solution {
private:
    class mycomparison {
    public:
        bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
            return lhs.second > rhs.second;
        }
    };
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        unordered_map<int, int> map;
        for (int i = 0; i < nums.size(); i ++) map[nums[i]] ++;
        
        priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que;

        for (unordered_map<int, int>::iterator it = map.begin(); it != map.end(); it ++) {
            pri_que.push(*it);
            if (pri_que.size() > k) pri_que.pop();
        }

        vector<int> res(k);
        for (int i = k - 1; i >=0; i --) {
            res[i] = pri_que.top().first;
            pri_que.pop();
        }

        return res;
    }
};

时间复杂度：O(nlogk)

空间复杂度：O(n)

总结

今天的两个题都是用于维护k个有序队列，一个是用于维护潜在满足题意的部分元素的单调队列，一个是用于维护队列完全有序的优先队列。

• 栈是容器适配器，底层容器使用不同的容器，导致栈内数据在内存中不一定是连续分布的。
• 用栈实现队列需要建立两个栈，用队列实现栈就用一个队列就能实现
• 操作系统中的目录也是用到了栈的数据结构，递归也是用到的栈，因此递归都能用栈实现