2018 BeijingGDG 一日游

Android

JetPack

官方框架，稳定，持续更新。

https://github.com/googlesamples/android-sunflower

https://developer.android.com/jetpack/

结论：应用开发，寻找替代框架的选择。

Kotlin

1、趋势明朗，Google 官网经过几年沉淀，Google 内部大规模使用。官方盖章。

2、比Java好用，而且开元代码很多都是用Kotlin来编写的。

结论：Kotlin 成为 Android 以后发展绕不开的技术。

技术优势细节：

Sequence 高效

协程，一部成“同步”：eg,2 个接口异步回调都完成时执行

简洁支持多个库

kotlion 空安全 
图片框架mcimage
兼容 第三方库

Android系统源码

查看 --> 记录博客 or 笔记 --> UML 类图 --> 形成知识体系

1、有目的阅读：日常工作中遇到、学习计划中。

2、在线阅读源码： http://androidxref.com/

下载地址：https://pan.baidu.com/s/1ngsZs

3、阅读工具推荐：Source Insight

如何阅读系统源码其他博客推荐：

罗升阳、邓凡平、Gityan、刘望舒

4、UML 类图推荐：

工具：https://www.processon.com/

时序图：Visio2013、Visio2016

 

聚美优品 待开源 性能优化组件

简单介绍：

悬浮窗、动态实时显示：activity 全类名，当前 application 网络流量、当前内存使用量、cpu。

可展示并修改全部的 sharedpreferences 

等等，是调试、测试利器。

特点：快捷 直观、

原理：参考 Android profile 插件 和其他 shell 命令。

对于线上版本的环境：可以设置密码 来触发此功能。

细节举例：获取 CPU 使用情况静态

top -n 1
top -n -d 1不延迟（有些手机需要同步获取）

 

音视频技术在短视频项目中的应用

直播、倒播、特效、倍速

粒子系统 核心OpenGL
肢体识别 尬舞机

视频、多媒体这块没有研究，上图了：

核心拿到原数据 对原数据进行加工

 

 

 

人对声音比对图像更敏感

 

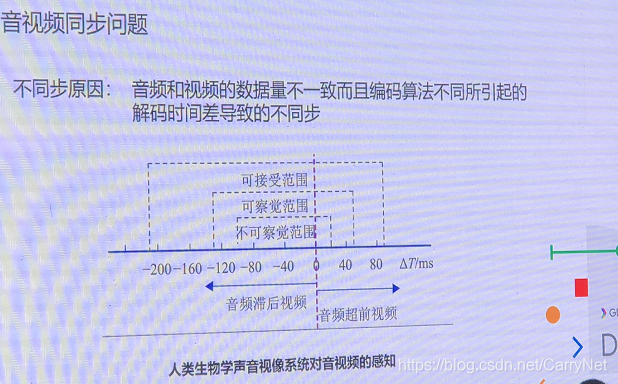
方案：以音频为主，原因：人类对音频敏感

 

TenosrFlow

现在深度学习状况，神经网络的发展历程与原理

人工智能的边界。

参考图灵机，给出的机器极限。

未来发发展与大规模发展应用趋势，在互联网行业中或者社会经济中的地位。

那些可以落地，那些还没有成熟未来可能会落地，哪些是人工智能边界外的东西。

神经网络，个人总结：

把机器像小孩子一样训练，让他学会某些技能，而不需要人力具体的建模。当然是在科学支持的界限内。