gSpan算法的研究多层索引文献引用判断图同构

口水话：疫情间看了论文《用多层索引判断图相似（中文翻译）》，里面的一个小细节提到了如何判断子图同构的问题。作者采用了gSpan（原文链接）原文链接2 简单版的算法，大体思路为：通过构造DFS代码树，不断地挖掘频繁子图的过程。

gspan是频繁子图挖掘算法，gsapn在图数据库中建立了一种新的字典序，并且把每一个图映射一个独特的最小DFS编码作为其规范化的标签。通过这个标签，gspan可以使用深度优先搜索去挖掘频繁联通子图。

问题定义：
gspan是为了挖掘满足一定支持度的联通子图。其中支持度定义：表示的是一个子图，有多少了图中包含这个子图。
前人方法缺点：
[4,5]中的FSG和AGM的方法利用了Apriorior[1]方法的优点。但是有俩个缺点
1 产生频繁项集。从k个频繁子图产生k+1个候选比项集本身更复杂、成本更高
2 修剪fasle positive的缺点：修剪假阳性图采用子图同构方法，但是子图同构的方法是NP-Complete问题，因此修剪假阳性图成本高。
而gspan算法直接将频繁子图的生长和频繁子图的检查放在一个步骤里面，加速了挖掘过程。

DFS subscripting:一个图可以进行多种DFS遍历，对应可以生成多个DFS树。但是这些树都是和原图子图同构（树怎么可能和图同构？）b-d三幅图是三种遍历算法生成的DFS树。

详细描述：

首先，根据每个图生成深度优先搜索树，依次列出这些搜索树的DFS编码。因为一个图有不同的深度优先搜索树，因此多种DFS编码。其中每种DFS编码都是按照字典序进行排列。文中使用DFS最小编码（DFS编码树的前序搜素）作为讨论的方案，DFS最小编码是第一种编码。
在图2中，给出图a，有深度优先搜索树bcd**[文献9]**，它们和a是同构的。

在表2中，给出了三种不同的DFS编码，它们对应图2bcd，加粗的边代表了图a三种不同的DFS树。其中编码的形成需要理解几个概念：

前向边：包含了DFS树中的所有边，从结束顶点开始增长，否则从其父节点增长
反向边：包含了不在DFS树中的边，从结束顶点依次和ID最小的顶点之间的边

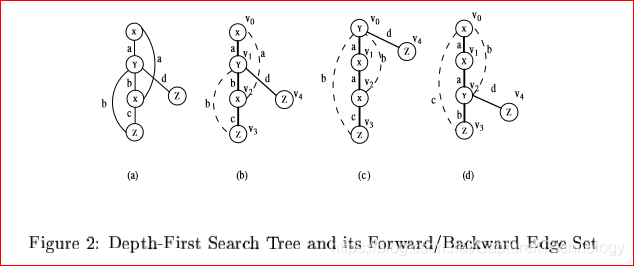
表1中每个DFS树生成DFS编码有一定的规则，俩条邻居边会满足如下的限制：1.若前一条边是反向边(（i,j.label(i),lable((i,j)),label(j)）中的i>j即为反向边，如(3,1,Z,b,Y)是一条反向边)，下一条边是反向边必须保证j+1 = (i) +1 且i+1 <=i ;若下一条边是前向边，则也满足类似的属性。定理如下：

表1中列出了一个图的三种DFS编码，在算法中仅仅使用最小的一个编码，即最小DFS编码（定义8）。

gSpan算法：

1. 根据数据库GS中顶点和边标签出现的频率给其排序；
2. 移除掉不频繁的顶点和边（不频繁：小于给定的支持度）
3. 按照频率的降序重新给顶点和边relabel
4. 将GS中所有频繁1边图放入S1
5. 按照DFS字典序（DFS字典序）排序S1中的元素

Step2: (算法8-9行) 对于1-边的频繁子图，子图挖掘增加（图1中）以1-边为根的子树的所有节点。

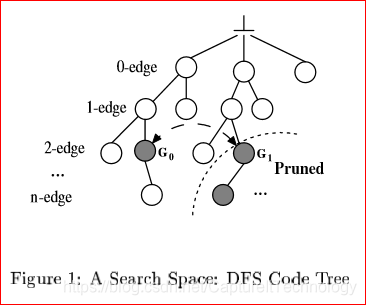
Step3: 依次挖掘1-边图的频繁子图，每次挖掘完一个边图的频繁子图之后，在原来的数据库中要把之前的1-边剔除掉。这一个过程将GS投影为含有更加少的顶点、边的小图，使得挖掘的过程更加迅速。

Step4:当所有的频繁1-边图和它们的后代都产生后算法停止。