【数据结构初阶】用堆解决TOP-K问题

🌟hello，各位读者大大们你们好呀🌟

🍭🍭系列专栏：【数据结构初阶】

✒️✒️本篇内容：top-k问题解决方法对比、最优方法（堆）代码实现

🚢🚢作者简介：计算机海洋的新进船长一枚，请多多指教( •̀֊•́ ) ̖́-

📡📡代码存放仓库：gitee码云-topk问题存放！

---

目录

🌳一、引言

🌳二、方法对比

🌳三、解决思路

🌵1. 用数据集合中前K个元素来建堆

🌵2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

🌳四、代码实现

🌵1.向下调整算法 

🌵2.建堆+遍历

🌵3.验证

---

一、引言

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。

---

二、方法对比

通过正常排序、建堆选数（a，b）两种方法的时间复杂度对比，我们可以得出结论：

建堆选数（b）方案更优。

---

三、解决思路

最佳的方式就是用堆来解决，基本思路如下： 

1. 用数据集合中前K个元素来建堆

• 前k个最大的元素，则建小堆
• 前k个最小的元素，则建大堆

2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

---

四、代码实现

下面以 N 个数求 K 个最大数为例子

1.向下调整算法 

void Swap(int* p1, int* p2)//位置交换函数
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void AdjustDown(int* a, int n, int parent)
{
	int minChild = parent * 2 + 1;//堆的性质
	while (minChild < n)
	{
		// 找出小的那个孩子
		//minChild + 1 < n —— 防止越界（出现没有右孩子的情况）
        //开始minChild是左孩子，判断后，小的孩子就是minChild
		if (minChild + 1 < n && a[minChild + 1] < a[minChild])
		{
			minChild++;
		}

		if (a[minChild] < a[parent])
		{
			Swap(&a[minChild], &a[parent]);//比较完后交换位置
			parent = minChild;
			minChild = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

2.建堆+遍历

void PrintTopK(int* a, int n, int k)
{
	// 1. 建堆--用a中前k个元素建堆
	int* kMinHeap = (int*)malloc(sizeof(int) * k);//开辟空间
	assert(kMinHeap);    //检验是否开辟失败
	for (int i = 0; i < k; ++i)//存数据
	{
		kMinHeap[i] = a[i];
	}
	for (int i = (k - 1 - 1) / 2; i >= 0; --i)//从第一个父亲节点开始向下调整
	{
		AdjustDown(kMinHeap, k, i);
	}

	// 2. 将剩余n-k个元素依次与堆顶元素交换，不满则则替换
	for (int j = k; j < n; ++j)
	{
		if (a[j] > kMinHeap[0])
		{
			kMinHeap[0] = a[j];
			AdjustDown(kMinHeap, k, 0);
		}
	}

	for (int i = 0; i < k; ++i)
	{
		printf("%d ", kMinHeap[i]);
	}
	printf("\n");
}

3.验证

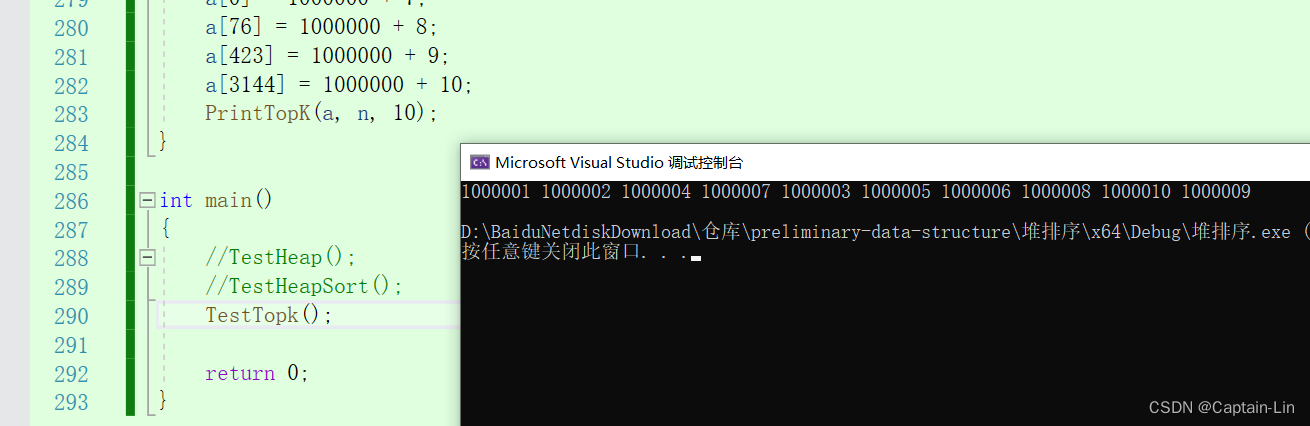
如果代码无误，会输出10个自定义的最大的数

//选最大的建小堆
void TestTopk()
{
	int n = 10000;
	int* a = (int*)malloc(sizeof(int) * n);//给a创立空间
	srand(time(0));    //生成随机数
	for (int i = 0; i < n; ++i)//避免有超过1000000的数出现，便于后面检验
	{
		a[i] = rand() % 1000000;
	}

	a[5] = 1000000 + 1;
	a[1231] = 1000000 + 2;
	a[531] = 1000000 + 3;
	a[5121] = 1000000 + 4;
	a[120] = 1000000 + 5;
	a[99] = 1000000 + 6;
	a[0] = 1000000 + 7;
	a[76] = 1000000 + 8;
	a[423] = 1000000 + 9;
	a[3144] = 1000000 + 10;

	PrintTopK(a, n, 10);//如果代码无误，会顺序输出上述10个最大的数
}

int main()
{
	TestTopk();

	return 0;
}

🌹🌹TOP-K问题的分析和解决方法大概就讲到这里啦，博主后续会继续更新数据结构初阶的其他内容，满满干货，如果觉得博主写的还不错的话，希望各位小伙伴不要吝啬手中的三连，你们的支持是博主坚持创作的动力！💪💪