1. 单链表实现代码
定义简单的单链表实现代码，里面定义单链表每个节点的组成形式，是一个内部类，实现了最基本的增、删、查、迭代器遍历功能。
package com.calarqiang.linear;
import java.util.Iterator;
/**
* @author calarqiang
* @create 2022-07-23-13:54
* 实现单向链表
*/
public class LinkList<T> implements Iterable<T> {
private int N;
private Node<T> head;
// 内部节点类
private class Node<T> {
private T elem;
private Node<T> next;
public Node(T elem, Node<T> next) {
this.elem = elem;
this.next = next;
}
}
public LinkList() {
this.N = 0;
// 初始化头结点
this.head = new Node(null, null);
}
// 获取元素个数
public int getLen() {
return this.N;
}
// 清空链表
public void clear() {
this.head = null;
this.N = 0;
}
// 在末尾插入一个元素
public void insert(T elem) {
Node newNode = new Node(elem, null);
// 寻找到最后一个节点
Node<T> p = head;
while (p.next != null) {
p = p.next;
}
p.next = newNode;
this.N++;
}
// 在链表指定索引处插入一个元素
public void insert(int index, T elem) {
// 判断插入位置是否合法
if (index < 0 || index > this.N) {
System.out.println("插入位置不合法！");
return;
}
Node newNode = new Node(elem, null);
// 找到该索引的上一个索引处元素
Node<T> p = head;
for (int i = 0; i <= index - 1; i++) {
p = p.next;
}
newNode.next = p.next;
p.next = newNode;
this.N++;
}
// 判断链表是否为空
public boolean isEmpty() {
return this.N == 0;
}
// 删除指定位置的元素
public T remove(int index) {
// 判断位置是否合法
if (index < 0 || index >= this.N) {
System.out.println("删除位置不合法！");
return null;
}
Node<T> p = head;
// 找到指定元素的上一个元素
for (int i = 0; i <= index - 1; i++) {
p = p.next;
}
// 用一个元素记录要删除的节点的值
T elem = p.next.elem;
p.next = p.next.next;
return elem;
}
// 寻找某个元素所在的索引处
public int getElem(T elem) {
Node<T> p = head;
for (int i = 0; p.next != null; i++) {
p = p.next;
if (p.elem.equals(elem)) {
return i;
}
}
// 没有找到，返回-1
return -1;
}
// 通过重写Iterable接口中的iterator方法来实现迭代器
@Override
public Iterator<T> iterator() {
return new MyIter();
}
// 编写一个内部类，来实现Iterator接口，并重写hasNext和next方法。
private class MyIter implements Iterator<T> {
private Node<T> cursor;
public MyIter() {
this.cursor = head;
}
@Override
public boolean hasNext() {
return this.cursor.next != null;
}
@Override
public T next() {
cursor = cursor.next;
return cursor.elem;
}
}
}
2. 单链表反转
原理：所谓链表反转，就是让原来的单链表指向发生变化，从左往右---->从右往左，指向发生反转。
定义两个重载方法，第一个方法对整个链表进行反转，第二个重载方法为反转单个节点的方法。
// 反转整个单链表
public void reverse() {
// 判断单链表是否为空，如果为空，就不需要反转
if (head.next == null) {
return;
}
// 调用反转节点方法，对每个节点进行反转
reverse(head.next);
}
// 反转每个结点
public Node<T> reverse(Node curr) {
// 递归退出条件
if (curr.next == null) {
head.next = curr;
curr.next = null;
return curr;
}
// 如果当前节点的下一个节点不为null，则反转下一个节点,这里返回的是要反转的节点的下一个节点，此时为当前反转的上一个节点了
Node prev = reverse(curr.next);
// 让原来的下一个节点变成当前节点的上一个节点，并让当前节点的下一个节点为null，返回当前节点
prev.next = curr;
curr.next = null;
return curr;
}
3. 快慢指针
字面意思，就是一个指针移动的快，一个指针移动的慢，通过这个两个指针移动的特点，就可以完成相应的需求。
可以通过快慢指针，完成下面几个需求。
3.1 寻找中间值
实现原理：初始时，快指针和慢指针均指向链表的头结点，快指针每次往后移动两个节点，慢指针每次往后移动一个位置，这样，快指针到达链表的尾部时，慢指针刚好到达链表的中点位置。
- 元素个数为奇数时，快指针可以走到奇数元素+1的位置，比如长度n=5时，快指针可以走到6的位置，刚好走6/2=3步，慢指针也就走到了第三个节点，正好是中间位置。
- 元素个数为偶数时，快指针可以走到偶数元素个数位置，比如长度n=4，快指针可以走到4的位置，刚好走4/2 = 2步，慢指针也就走到了第二个节点，也是中间位置。
实现代码
public T findCenter(){
// 初始化快慢指针
Node<T> fast = head,slow = head;
// 快慢指针移动条件
while(fast!=null && fast.next!=null){
fast = fast.next.next;
slow = slow.next;
}
// 返回慢指针指向的值（中间值）
return slow.elem;
}
3.2 判断单链表是否有环
后面的测试都是基于环来判断，前面单链表的创建直接使用尾插法，因此这里重新定义一个单链表结构，方便下面应用的测试。
public class LinkListCircle<T> {
private Node<T> head;
public LinkListCircle() {
this.head = new Node<>(null, null);
}
private class Node<T> {
private T elem;
private Node<T> next;
public Node(T elem, Node<T> next) {
this.elem = elem;
this.next = next;
}
public void setNext(Node<T> node) {
this.next = node;
}
}
public void createCircle() {
Node<Integer> a = new Node<>(1, null);
Node<Integer> b = new Node<>(2, null);
Node<Integer> c = new Node<>(3, null);
Node<Integer> d = new Node<>(4, null);
Node<Integer> e = new Node<>(5, null);
Node<Integer> f = new Node<>(6, null);
a.next = b;
b.next = c;
c.next = d;
d.next = e;
e.next = f;
f.next = b;
head.setNext((Node<T>) a);
}
}
有时候单链表会存在环的情况，此时会有两种类型的环，一种类型是“6”字型，另一种是“O”字型号（循环单链表）。但是实现的逻辑都是采用快慢指针来实现，因为快指针比慢指针每次多走一个结点，因此总有一个时刻，它们会相遇【证明参考：证明】，如果相遇，则证明有环，反之，如果快指针指向空了，那么就证明没有环存在。
简单证明：参考这里
“6字型”
第一次移动
第二次移动
第三次移动 【重合】
“O字型”
第一次移动
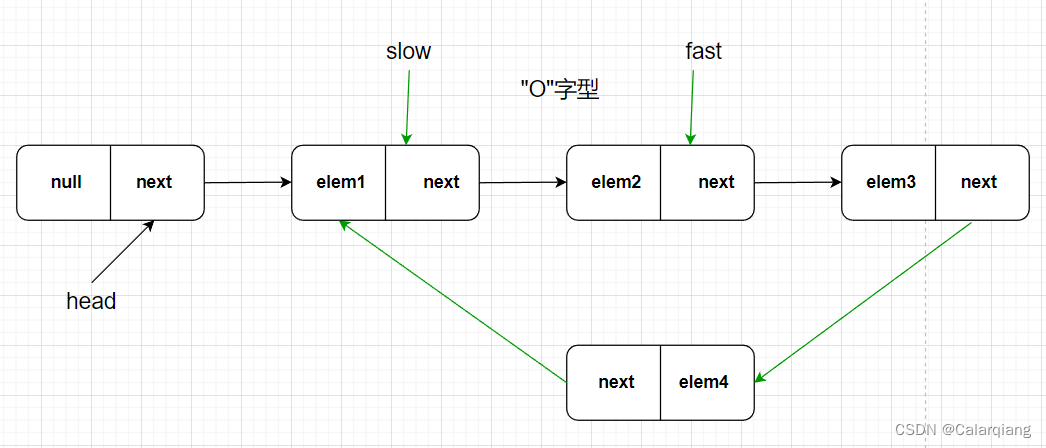
第二次移动
第三次移动
第四次移动【重合】
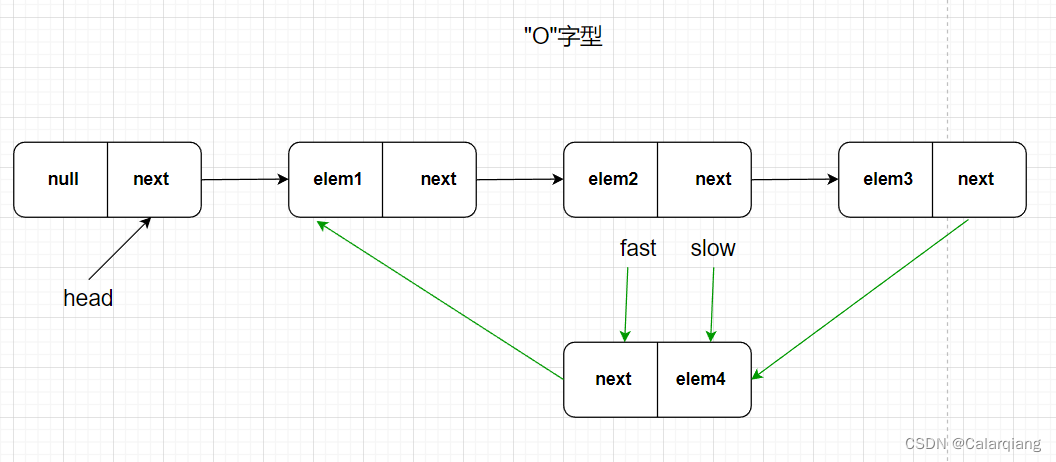
实现代码：
public boolean isCircle(){
//定义快慢指针
Node<T> fast=head,slow = head;
// 循环条件，快指针指向元素或下一个元素不能为null
while(fast!=null && fast.next!=null){
fast = fast.next.next;
slow = slow.next;
// 判断快慢指针是否相遇
if(Objects.equals(fast,slow)){
return true;
}
}
return false;
}
3.3 有环单链表的入口
如果单链表存在环，那么环的入口在哪里？怎样找到它？也是采用快慢指针的方式，当快指针和慢指针第一次重合之后，重新让一个指针指向入口处，然后让原来慢指针与其同步移动，当二者相遇时，即为入口处。具体证明参见这里。单链表入口原理解释
代码实现
public T findEntrance() {
Node<T> fast = head, slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
// 判断二者是否相遇，相遇，有环，可以继续寻找入口元素
if (Objects.equals(fast, slow)) {
// 相遇之后，再生成一个指针，指向头指针,然后原来慢指针和现在新指针同步走动
Node<T> p = head;
// 快慢指针同步移动，直到相遇
while (!Objects.equals(p, slow)) {
p = p.next;
slow = slow.next;
}
// 找到入口了，结束方法
return p.elem;
}
}
// 没有环，返回null
return null;
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
