队内最终筛选

最新推荐文章于 2025-07-19 21:53:13 发布

原创最新推荐文章于 2025-07-19 21:53:13 发布 · 143 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构 #dfs

ACM训练2021 专栏收录该内容

43 篇文章

订阅专栏

队内最终筛选

导语
涉及的知识点

导语

经过这次选拔，意识到自己和他人的差距实在是太大了，需要沉下心来好好思考，好好练习

涉及的知识点

本次选拔涉及到的知识点多且广泛，在此不一一列出

题目

简单签到

在这里插入图片描述

思路：整数分块模板题

代码

#include <iostream>
using namespace std;
typedef long long ll;
ll n,l,ans;
int main() {
    scanf("%lld",&n);//录入数据
    l=n;
    for (long long i=2; 1ll*i*i<=n; i++) {
        long long x=l-(n/i);
        ans=(ans+((i-1)*x%998244353))%998244353;
        l=n/i;
    }
    for (long long i=1; i<=l; i++)
        ans=(ans+(n/i)%998244353)%998244353;
    printf("%lld\n",ans);
    return 0;
}

暴力解题

在这里插入图片描述

思路：直接模拟这个过程，数出它是怎么通关的

代码

#include <bits/stdc++.h>
using namespace std;
int main()
{
    ios::sync_with_stdio(0),cin.tie(0);
    cin >>N;
    for(int i=1; i<=N; i++)
    {
        ll t;
        cin >>t;
        ans+=i*(t-1)+1;
    }
    cout <<ans;
    return 0;
}

打弹珠

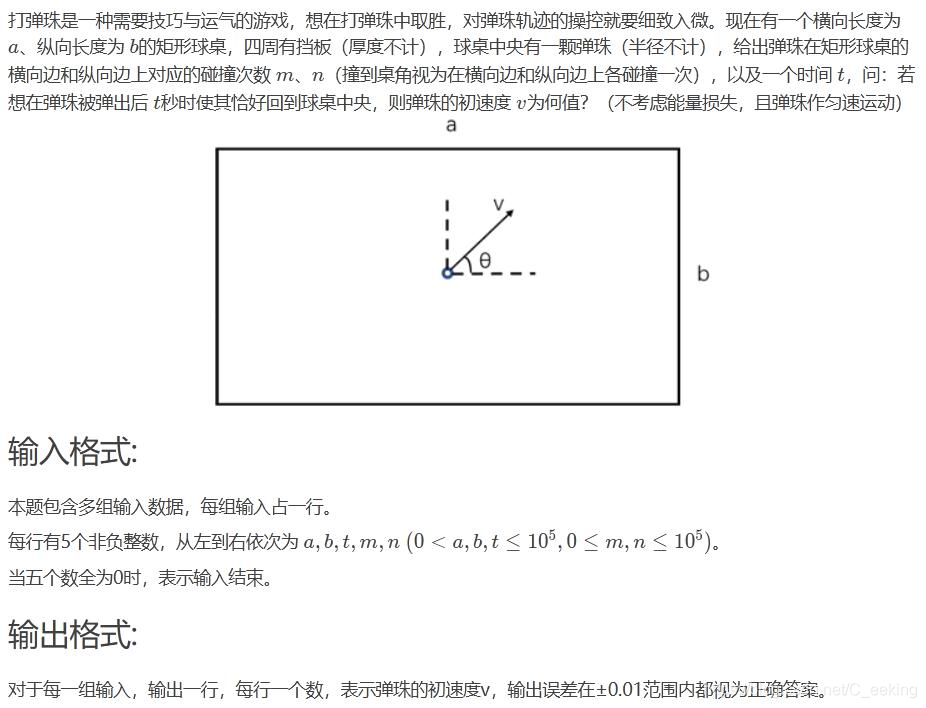
在这里插入图片描述

思路：对于弹珠，如果最后能弹回来，观察它的轨迹并进行拓展平移，最后可以得到如图所示的结论

如图：

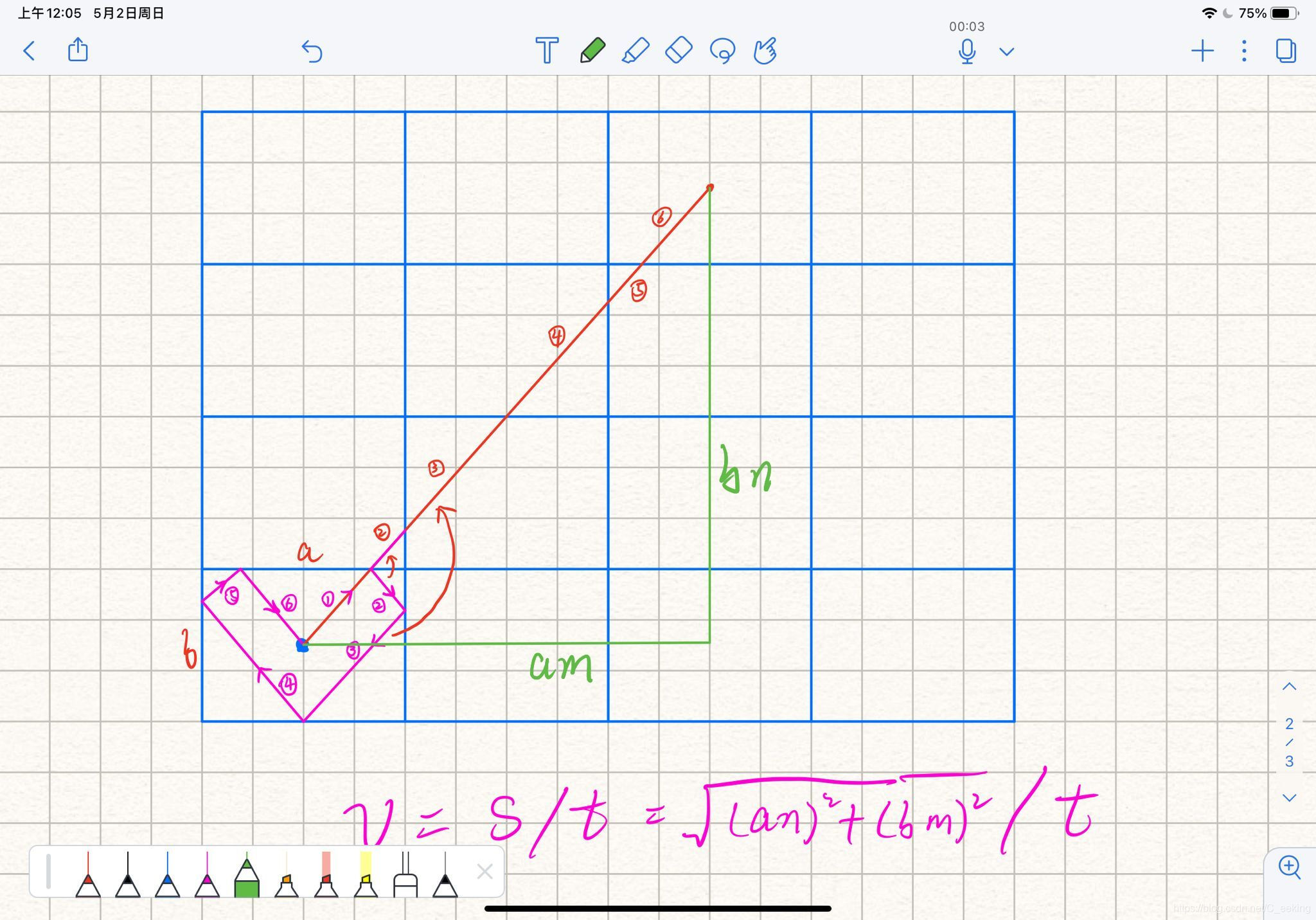
在这里插入图片描述

代码

#include <bits/stdc++.h>
using namespace std;
int main() {
    long long a,b,t,m,n;
    while(scanf("%lld %lld %lld %lld %lld",&a,&b,&t,&m,&n)) {
        if(a==0&&b==0&&t==0&&m==0&&n==0)
            break;
        printf("%lf\n",sqrt((double)b*m*b*m+(double)a*n*a*n)/t);
    }
}

有趣的骰子

在这里插入图片描述

思路：运用一般的思路，答案即 $1-\frac{1}{n^m}=\frac{n^m-1}{n^m}$ ，但是数据过大，首先需要用快速幂算出 $n^m$ ，因为是取模运算，所以之后用可以用乘法逆元算出 $\frac{1}{n^m}$

代码

#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9+7;
int qpow(int a, int b, int p) {
    int ans = 1 % p;
    for(; b; b >>= 1) {
        if(b & 1)
            ans = (long long)ans * a % p;
        a = (long long)a * a % p;
    }
    return ans;
}
int main() {
    int t, m, n;
    cin >> t;
    while(t--) {
        cin >> n >> m;
        int sum = qpow(n,m,mod);//n的m次方
        int ans = (sum - 1LL) * qpow(sum,mod-2,mod) % mod;
        //费马小定理求乘法逆元
        cout << ans << "\n";
    }
}

静静的难题

在这里插入图片描述
思路：做这道题的时候思路被限制住了，只想着用类似搜索的思想来实现，实际上，交换的操作使得a串可以分解为一个个字母，通过排列组合来获得b串，只需要判断以b为目标时，a的字符够不够用以及a的字符经过变化之后是否有多余

代码

#include <bits/stdc++.h>
using namespace std;
int t,n,m,na[30],nb[30];
string a,b;
int main() {
    scanf("%d", &t);
    while(t--) {
        scanf("%d%d",&n,&m);
        memset(na,0,sizeof na);
        memset(nb,0,sizeof nb);
        cin >> a >> b;
        for(int i=0; i<n; i++) {
            na[a[i]-'a']++;
            nb[b[i]-'a']++;
        }//记录字母数量
        int flag=1,left=0;//left记录
        //对于当前字母A来说比A小1的字母用剩了多少个
        for(int i=0; i<26; i++) {
            if(na[i]+left<nb[i]) {
                flag=0;
                break;
            }//如果剩下的字母加上当前字母不足得到b对应字母的数量
            left=na[i]+left-nb[i];//获得剩下的字母数
            if(left%m!=0) {//如果用不完，代表有字母不能转换，是多的
                flag=0;
                break;
            }
        }
        if(flag)
            cout << "Yes" << endl;
        else
            cout << "No" << endl;
    }
    return 0;
}

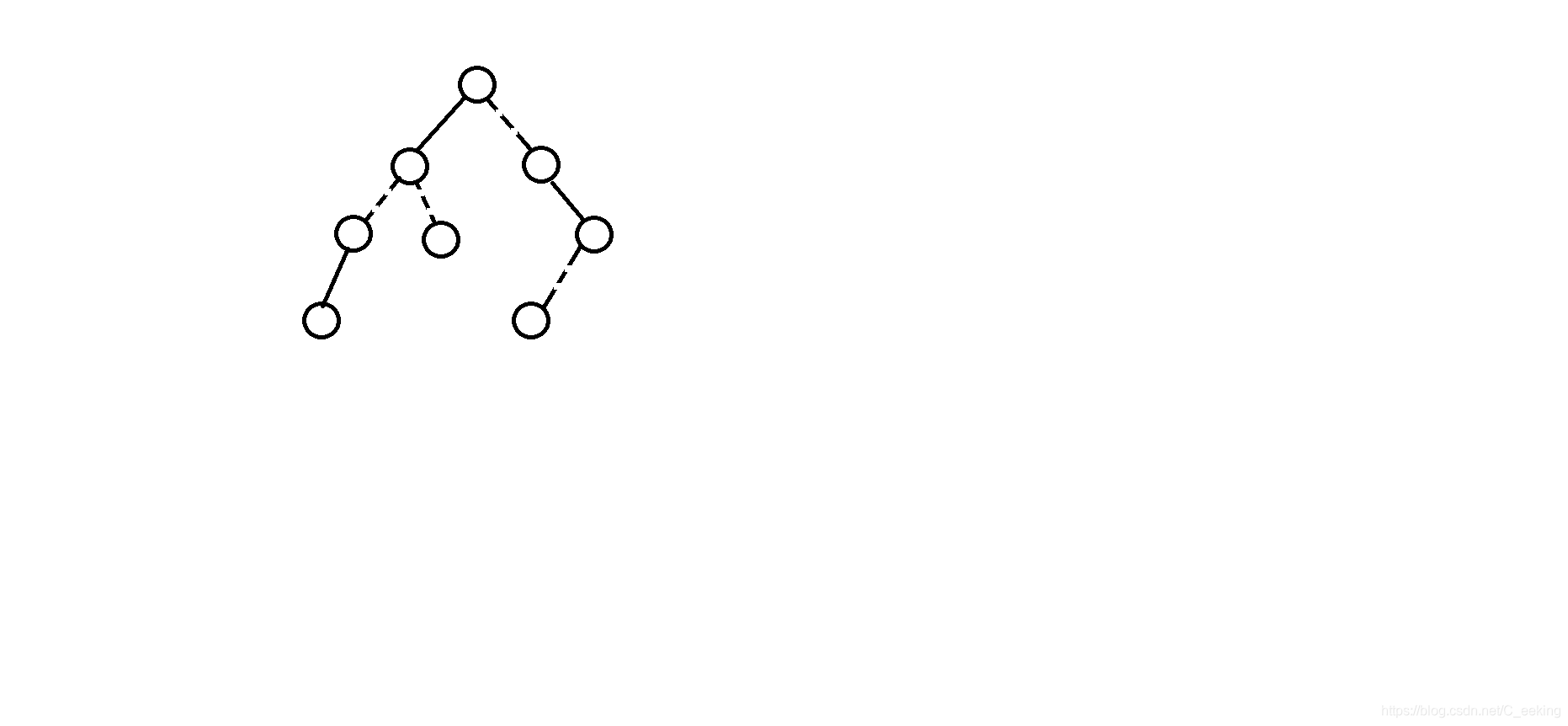
天空之城

在这里插入图片描述
思路：单纯的DFS加上一点技巧，处于同一条支路上的断桥被视为一个整体，对于每个点A，遍历它的子支路，统计其中的存在断桥的支路，每次搜索返回A的子支路的子支路断桥个数和与A相邻的子支路的状态（1或0）

如图
在这里插入图片描述

代码

#include <bits/stdc++.h>
using namespace std;
struct node {
    int v, w; //w=1:broken w=0:well
};
vector<node>edge[100010];
bool vis[100010];
int dfs(int s) {
    vis[s]=1;
    int res=0;
    for(auto e:edge[s])
        if(!vis[e.v])
            res+=max(e.w, dfs(e.v));
    return res;
}
int main() {
    int T, n, u, v, w;
    scanf("%d",&T);
    while(T--) {
        scanf("%d",&n);
        memset(vis,0,sizeof(vis));
        for(int i=1; i<=n; i++)//清空图
            edge[i].clear();
        for(int i=0; i<n-1; i++) {
            scanf("%d%d%d",&u,&v,&w);
            edge[u].push_back(node{v, w});//存树
            edge[v].push_back(node{u, w});
        }
        printf("%d\n",dfs(1));//从第一个点开始搜
    }
    return 0;
}

长颈鹿找朋友

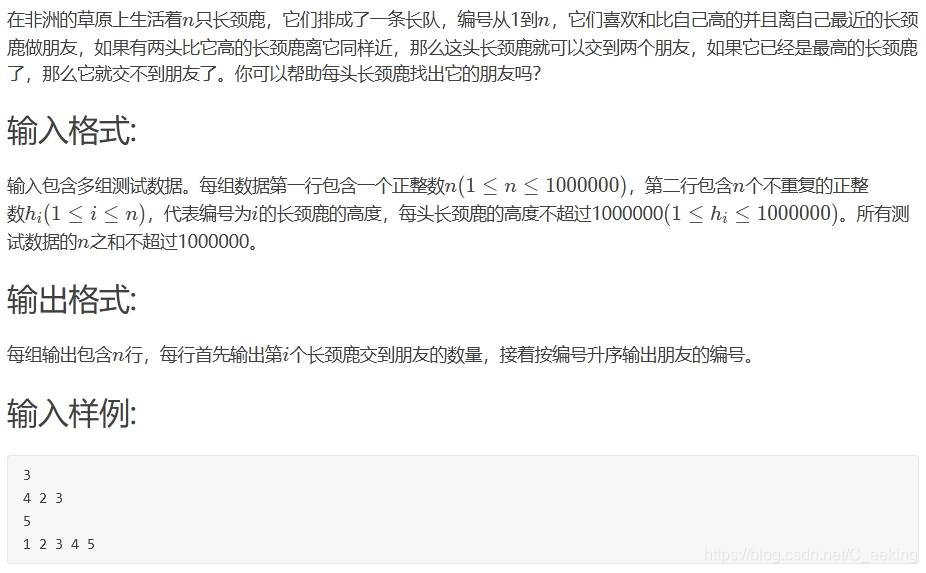
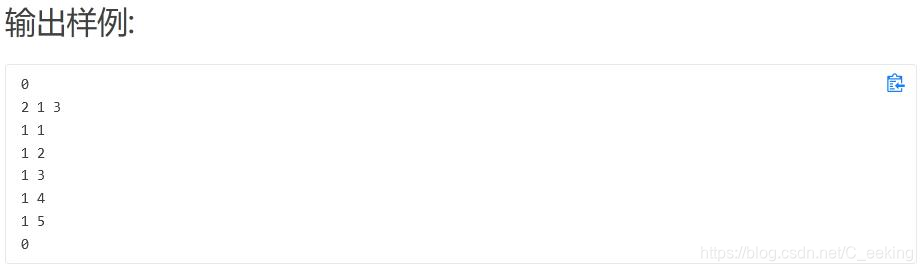
在这里插入图片描述
思路：使用单调栈保存坐标，但是用坐标对应的实值大小来判断是否需要入栈，具体看代码

代码

#include <bits/stdc++.h>
using namespace std;
int const maxn=1e6+7;
int n,a[maxn],l[maxn],r[maxn];
int main() {
    while(~scanf("%d",&n)) {
        stack<int>s;//使用单调栈
        memset(l,-1,sizeof(l));
        memset(r,-1,sizeof(r));//初始化为-1
        for(int i=1; i<=n; i++) {
            scanf("%d",a+i);
            if(s.empty())//栈空直接入栈
                s.push(i);
            else {
                while(!s.empty()) {
                    int tmp=s.top();
                    if(a[tmp]>a[i]) {//如果栈顶大于扫描值
                    //说明栈顶是当前扫描值的左最近
                        l[i]=tmp;
                        break;
                    }
                    s.pop();//如果栈顶不是，则弹出直到为空
                    //或找到满足条件的值
                    r[tmp]=i;//扫描值为栈中小于扫描值的右值
                }
                s.push(i);
            }
        }
        for(int i=1; i<=n; i++) {
            if(l[i]==-1) {
                if(r[i]==-1)
                    printf("0\n");
                else
                    printf("1 %d\n",r[i]);
            } else {
                if(r[i]==-1)
                    printf("1 %d\n",l[i]);
                else {
                    if(i-l[i]==r[i]-i)
                        printf("2 %d %d\n",l[i],r[i]);
                    else if(i-l[i]<r[i]-i)
                        printf("1 %d\n",l[i]);
                    else
                        printf("1 %d\n",r[i]);
                }
            }
        }
    }
    return 0;
}

静静的异世之旅

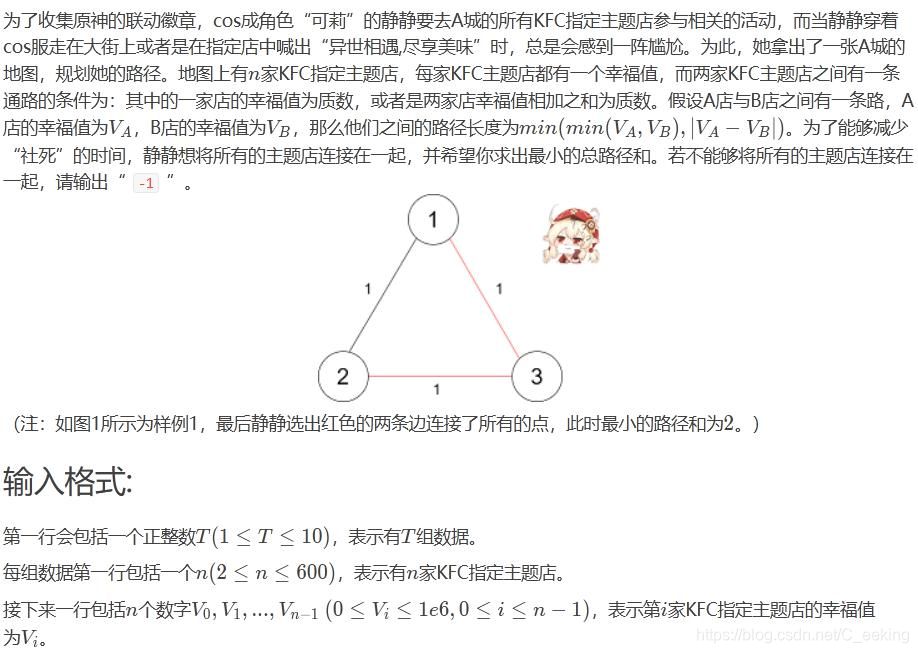
在这里插入图片描述
思路：最小生成树的模板题，只不过是在边的选择上加了一点技巧

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 4e5 + 7;
int head[maxn], nxt[maxn], ver[maxn], wi[maxn], tot;
bool vis[maxn];
int a[maxn], n;
void adde(int u, int v, int w) {
    ++tot;
    ver[tot] = v;
    wi[tot] = w;
    nxt[tot] = head[u];
    head[u] = tot;
}
void init() {
    for (int i=0; i<=n; i++) {
        head[i] = 0;
        vis[i] = false;
    }
    tot = 0;
}
bool isprime(int x) {
    if (x == 0 || x == 1)
        return false;
    if (x == 2 || x == 3)
        return true;
    bool flag = true;
    for (int i=2; i<=(int)sqrt(x); i++) {
        if (x % i == 0) {
            flag = false;
            break;
        }
    }
    return flag;
}
int prim() {
    priority_queue <pair<int, int> > q;
    q.push({0, 1});
    int num = 0, ans = 0;
    bool flag = false;
    while (!q.empty()) {
        int h = q.top().second, res = -q.top().first;
        q.pop();
        if (vis[h])
            continue;
        vis[h] = true;
        num ++;
        ans += res;
        if (num == n) {
            flag = true;
            break;
        }
        for (int i=head[h]; i; i=nxt[i]) {
            int v = ver[i];
            if (vis[v])
                continue;
            q.push({-wi[i], v});
        }
    }
    return flag?ans:-1;
}
int main() {
    int t;
    scanf("%d", &t);
    while (t --) {
        scanf("%d", &n);
        init();
        for (int i=1; i<=n; i++)
            scanf("%d", &a[i]);
        for (int i=1; i<=n; i++) {
            for (int j=i+1; j<=n; j++) {
                if (isprime(a[i]) || isprime(a[j]) || isprime(a[i] + a[j])) {
                    int w = min({a[i], a[j], abs(a[i] - a[j])});
                    adde(i, j, w);
                    adde(j, i, w);
                }
            }
        }
        int ans = prim();
        printf("%d\n", ans);
    }
    return 0;
}

颜色计数

在这里插入图片描述

思路：本题给了一个很关键的条件：保证每次询问区间右移且更大，这就可以让我们用两个指针，通过遍历输入数据+桶，记录已经出现的数据，清除不在范围内的数据，具体看代码

代码

#include <bits/stdc++.h>
using namespace std;
int const maxn=1e6+7;
int n, m, num[1000010], a[1000010], ans;
inline void add(int x) {
    num[x]++;//数量增加
    if (num[x] == 1)//如果是第一次增加，计数
        ++ans;
}
inline void mis(int x) {
    num[x]--;//当前数不属于查找范围内
    if (num[x] == 0)//如果-1后计数为0，代表在l~r的区间内没有x这个值
        --ans;
}
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i)
        scanf("%d", a + i);
    int l = 0, r = 0, lq, rq;
    ans = 0;
    while (m--) {
        scanf("%d%d", &lq, &rq);
        while (r < rq)//对r~rq内的粉笔操作，记录0~r内值
            add(a[++r]);//增加数量
        while (l < lq)//清除不属于lq~rq的数据
            mis(a[l++]);
        printf("%d\n", ans);
    }
    return 0;
}

四面不环海

在这里插入图片描述
思路：使用DFS的思想获取以每个点为顶的相邻河流长度，因为求最值，所以每次只取最大值即可，用DP的思想：保留已算出的结果&使用状态方程获取最值

代码

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
int r,c,mp[3050][3050];
int dp[3050][3050];
int dx[]= {-1,1,0,0};
int dy[]= {0,0,-1,1};
int DP(int x,int y) {
    if(dp[x][y]!=0)
        return dp[x][y];
    int MAX = 0;
    for(int k=0; k<4; k++) {
        int nx = x+dx[k];
        int ny = y+dy[k];
        if(mp[nx][ny]<mp[x][y]&&nx>=1&&ny>=1&&nx<=r&&ny<=c) {//如果相邻点小于该值，搜索该相邻点
            if(DP(nx,ny)>MAX)//获得相邻点构造河流长度的最大值
                MAX = DP(nx,ny);
        }
    }
    dp[x][y] = MAX+1;//加上自己
    return dp[x][y];
}
int main() {
    cin>>r>>c;
    for(int i=1; i<=r; i++)
        for(int j=1; j<=c; j++)
            cin>>mp[i][j];//录入数据
    int MAX = 0;
    for(int i=1; i<=r; i++)
        for(int j=1; j<=c; j++)
            if(DP(i,j)>MAX)//计算当以该点为顶的时候的值
                MAX = DP(i,j);
    cout<<MAX<<endl;
    return 0;
}