数据结构之选择排序 （算法思想、复杂度分析）

选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。

但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

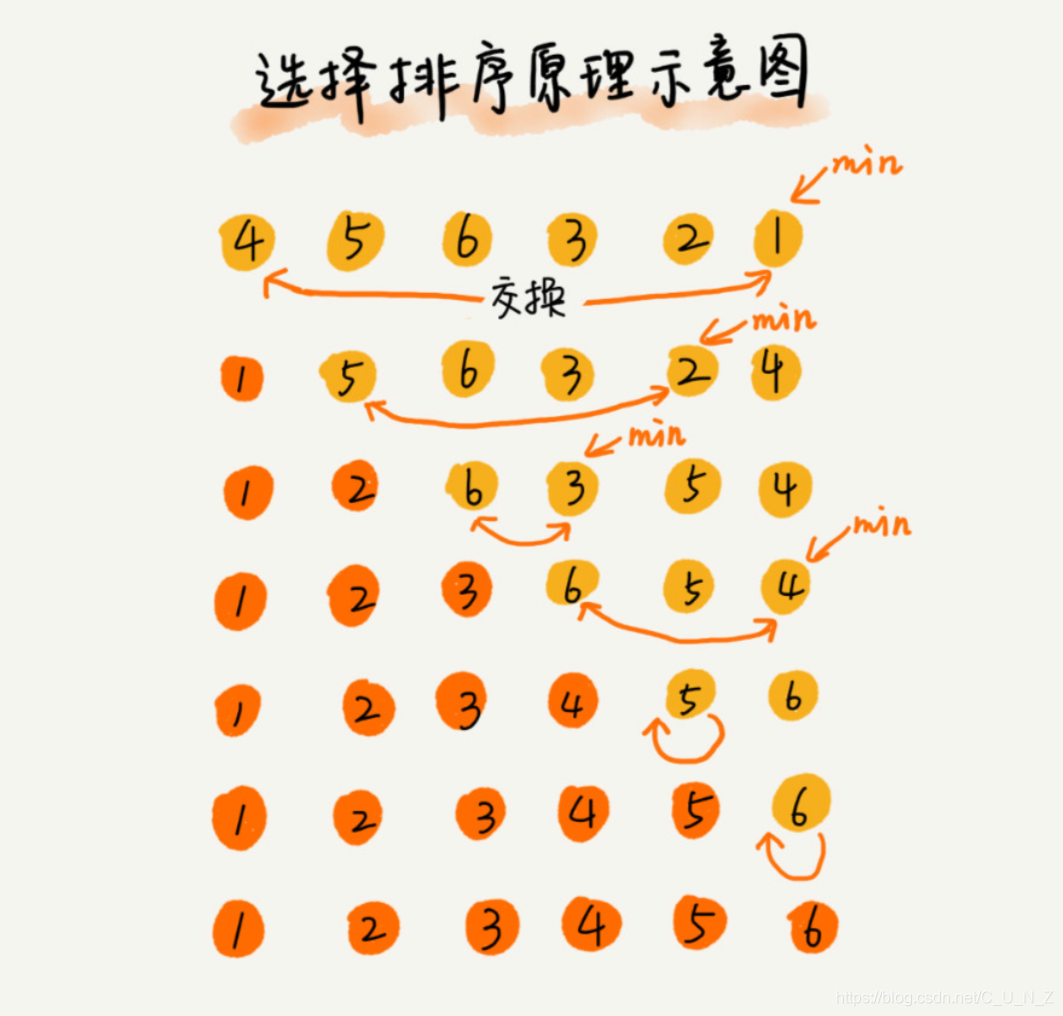
eg：代码实现：

public static void selectionSort(int[] array){
    int n = array.length;
    if(n <= 1){
        return;
    }else{
        for(int i = 0;i < n - 1;i++){
            int minIndex = i;
            for(int j = i+1;j < n;j++){
                if(array[j] < array[minIndex]){
                    minIndex = j;
                }
            }
            //此时minIndex对于的元素一定是当前未排序区间的最小值
            int temp = array[i];
            array[i] = array[minIndex];
            array[minIndex] = temp;
        }
    }
}

空间复杂度、时间复杂度：

• 选择排序空间复杂度为 O(1)，是⼀一种原地排序算法。
• 选择排序的最好情况时间复杂度、最坏情况和平均情况时间复杂度都为
  O(n^2)。
• 选择排序是一种不稳定的排序算法。
  选择排序每次都要找剩余未排序元素中的最小值，并和前面的元素交换位置，这样破坏了稳定性。

比如 5，8，5，2，9 这样一组数据，⽤用选择排序算法来排序的话，第一次找到最小元素 2，与第一个5 交换位置，那第一个 5 和中间的 5 顺序就变了，所以就不稳定了。

正是因此，相对于冒泡排序和插入排序，选择排序就相对较差了。