利用完全二叉树的性质，如何创建一个大根堆和一个小根堆？

原创已于 2023-04-22 20:22:39 修改 · 2.5k 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #堆 #完全二叉树

于 2022-08-06 12:58:31 首次发布

本文介绍了大根堆和小根堆的概念，并提供了Java实现的代码示例。大根堆中每个节点的值都不大于其父节点，而小根堆则是每个节点的值不小于其父节点。通过调整过程确保堆的性质，这两个数据结构常用于优先队列和排序算法中。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

大根堆

大根堆：每个结点的值不大于他的父亲结点的值

分析如下：

假设对{ 27,15,19,18,28,34,65,49,25,37 }这样一个集合的数据创建成堆；

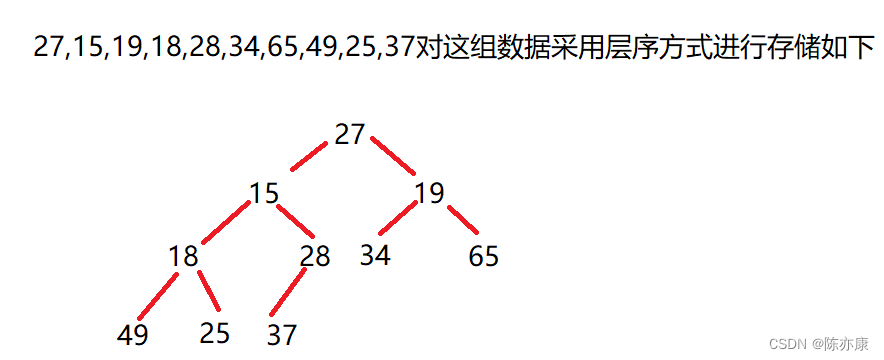
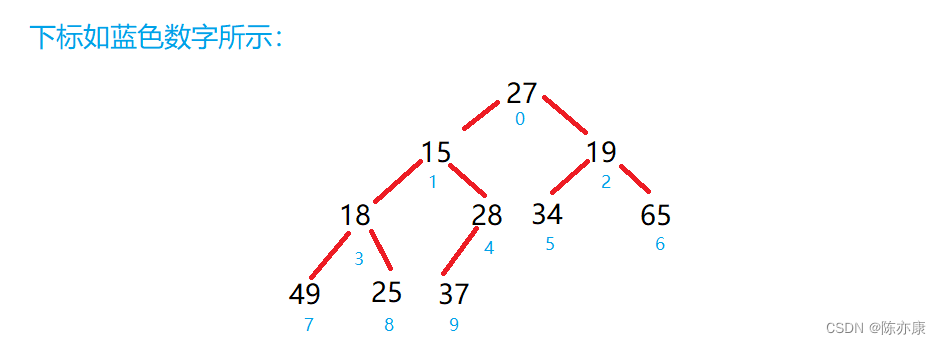
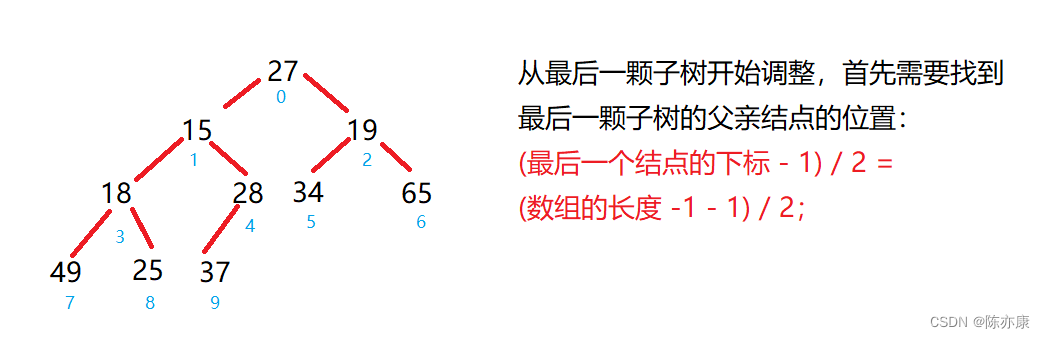
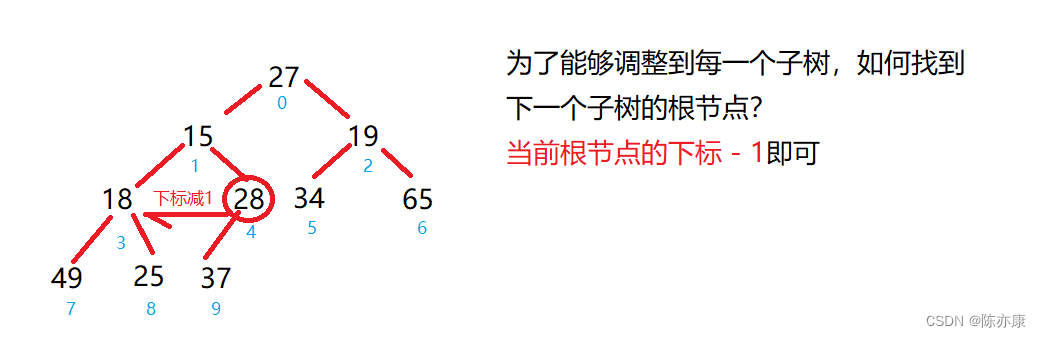
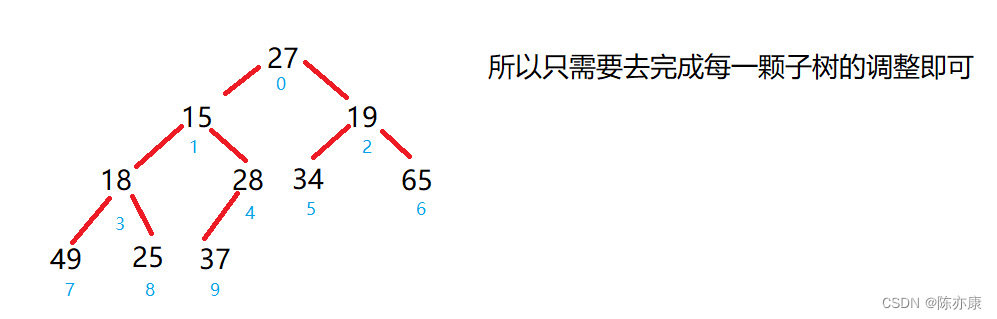
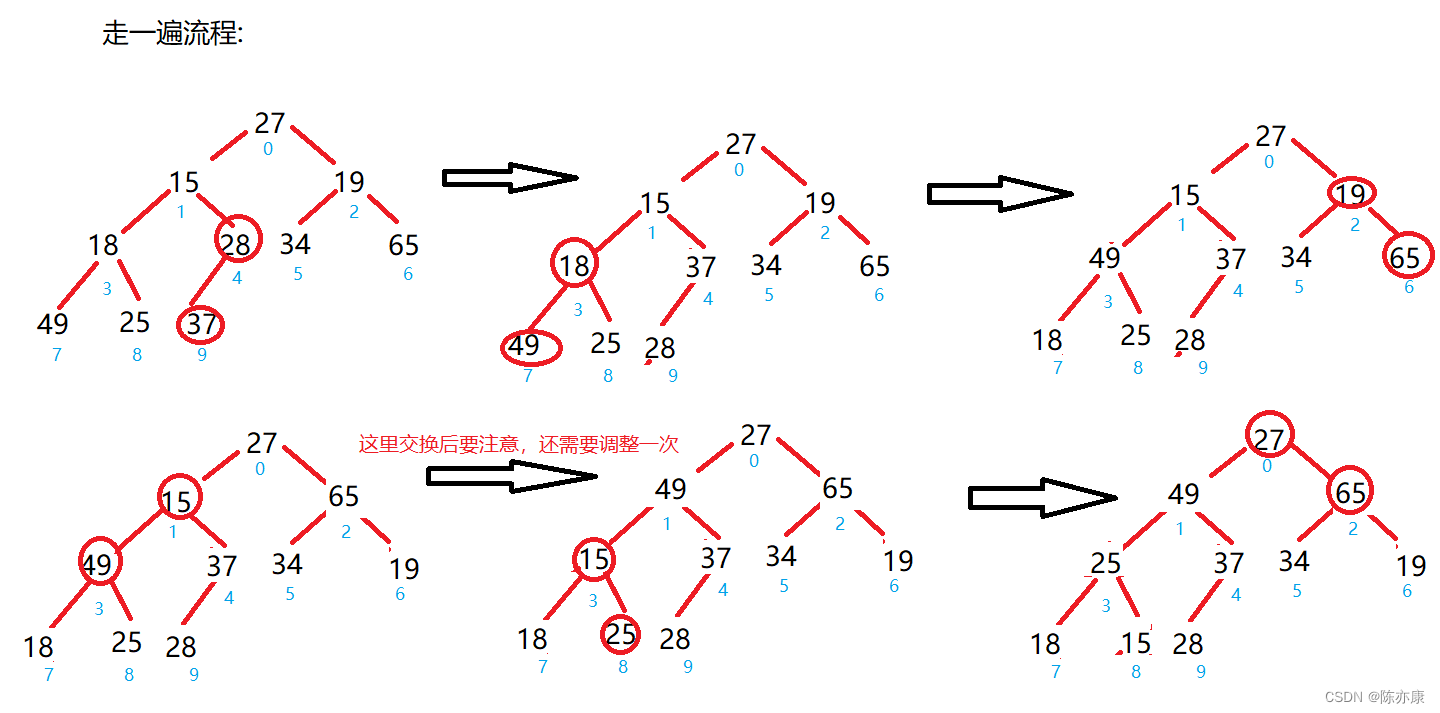
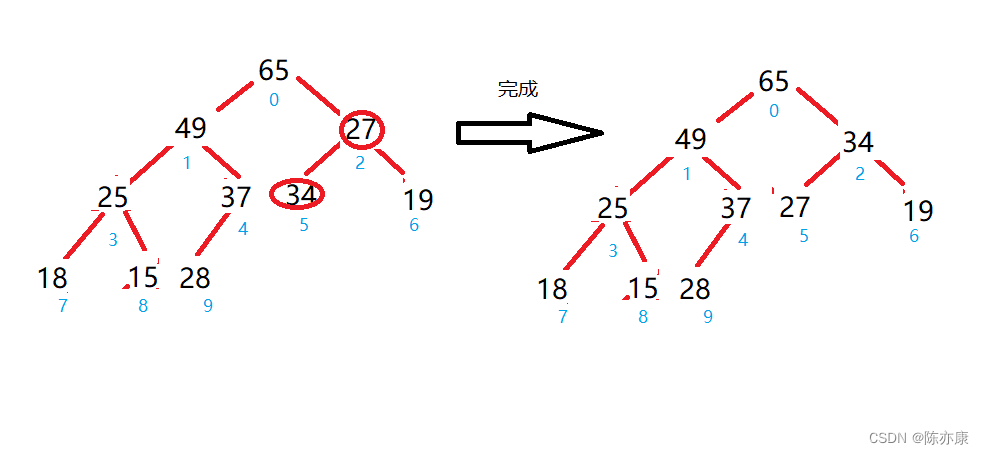
代码如下：

//建立大根堆
public class TestHeap{
    public int[] array;
    public int usedSize;//当前有效数组长度
    public TestHeap(){
        this.array = new int[10];
        this.usedSize = 0;
    }
    //初始化数组
    public void InitArray(int[] arrayClone){
        array = Arrays.copyOf(arrayClone, arrayClone.length);
        usedSize = array.length;
    }
    //创建大根堆
    public void createHeap(){
        for(int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--){
            adjustment(parent, usedSize);
        }
    }
    //调整
    public void adjustment(int parent, int len){
        //左子树结点下标
        int child = parent * 2 + 1;
        //调整
        while(child < len){
            //先判断有没有右孩子，如果右，找出最大值
            if(child + 1 < len && array[child] < array[child + 1]){
                child++;//如果右子树大，child++就指向他，如果左子树大，就不用管,直接进行下一步判断交换
            }
            //若左右子树的最大值大于父亲结点则交换
            if(array[child] > array[parent]){
                swap(array, child, parent);
                parent = child;
                child = parent * 2 + 1;
            } else{
                break;
            }
        }
    }
    //交换
    public void swap(int[] array, int child, int parent){
        int tmp = array[child];
        array[child] = array[parent];
        array[parent] = tmp;
    }
}

小根堆

小根堆：每个结点的值不小于他的父亲结点的值

分析与大根堆类似，只是比较出更小的进行替换

代码如下：

//建立大根堆
public class TestHeap{
    public int[] array;
    public int usedSize;//当前有效数组长度
    public TestHeap(){
        this.array = new int[10];
        this.usedSize = 0;
    }
    //初始化数组
    public void InitArray(int[] arrayClone){
        array = Arrays.copyOf(arrayClone, arrayClone.length);
        usedSize = array.length;
    }
    //创建大根堆
    public void createHeap(){
        for(int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--){
            adjustment(parent, usedSize);
        }
    }
    //调整
    public void adjustment(int parent, int len){
        //左子树结点下标
        int child = parent * 2 + 1;
        //调整
        while(child < len){
            //先判断有没有右孩子，如果右，找出最小值
            if(child + 1 < len && array[child] > array[child + 1]){
                child++;//如果右子树小，child++就指向他，如果左子树小，就不用管,直接进行下一步判断交换
            }
            //若左右子树的最大值小于父亲结点则交换
            if(array[child] < array[parent]){
                swap(array, child, parent);
                parent = child;
                child = parent * 2 + 1;
            } else{
                break;
            }
        }
    }
    //交换
    public void swap(int[] array, int child, int parent){
        int tmp = array[child];
        array[child] = array[parent];
        array[parent] = tmp;
    }
}