干货 | 基于深度强化学习的轨迹规划（附代码解读）

作者 | Vision 编辑 | 自动驾驶之心

 原文链接：https://zhuanlan.zhihu.com/p/1933268710770074901

点击下方卡片，关注“自动驾驶之心”公众号

戳我-> 领取自动驾驶近15个方向学习路线

>>自动驾驶前沿信息获取→自动驾驶之心知识星球

本文只做学术分享，如有侵权，联系删文

背景

随着业界鼓吹端到端自动驾驶一年之后，最近又开始宣传vla和强化学习的等新的技术范式。vla概念来自最近一年业界巨火的具身智能领域，本质上跟端到端的自动驾驶没有很明确的区别。本篇文章我们聚焦下强化学习这个技术范式。其实早在机器人领域早期，就有强化学习的身影，但一直由于其训练效率低下，复杂度高，在工业界一直没有很广泛的运用。随着2018年alpha zero 围棋比赛，2023年chatgpt rlhf的推出，2025年初 deepseek-o1 在线推理的推出，强化学习在各个行业和技术领域凸显出更广泛的使用潜力。在本着技术好奇的角度，结合最近两周对相关基础知识的理解，来讲讲作为一个计算机视觉（cv）背景的眼中，强化学习是个什么概念。故下面很多概念类比可能拿cv领域的知识来做类比。

基本大概念

监督式学习

自动驾驶里的感知任务，比如目标检测（分类回归）等就是一个明确的监督式任务，即给定好的数据输入和对应的监督信号，利用海量数据模拟一个函数将输入映射到输出。整个过程就是一个不断优化参数模型，期望找到一个固定数据（训练集）下的最优输出。一般利用平均均方误差值来表示。

模仿学习

类似于监督式学习，只不过模型输出的值更多是action（动作）。直观类似小孩学大人拿东西一样，对于同样的输入，大人怎么拿苹果，小孩就学习去拿。小孩的整个学习过程，就像以大人的动作作为监督信号，怎么去训练一个监督式学习的模型来使得模型输出的结果跟监督的动作信号一致，这种行为字面解释上就很像行为克隆（behavior cloning）。在自动驾驶中，有时候会把这个action扩展为一整条短时序下的轨迹。这个也是目前业界端到端自动驾驶里的最主要的学习目标。

强化学习

区别于模仿学习的直接反馈，强化学习更多是学习如何在与环境交互的过程中通过最后任务的结果来使告诉深度学习模型该怎么优化。本质是通过动态修改数据分布的方式来使得达到最优目标。从定义中可以看到，强化学习一般是一个时序决策任务，跟模仿学习不一样，前者类似有点延迟满足，后者是即时反馈。自动驾驶轨迹规划任务就是一个时序决策行为（每条轨迹都带着时间规划的信息），故目标就在动态环境交互过程中来使得轨迹更好（不冲出路沿外/不与其他车发生完全碰撞等）。规划迭代过程中会利用一些奖励信号（reward）来引导模型关注模型当前得到的结果如何。

逆强化学习

强化学习是通过动态reward的方式来指导模型学习，但一般很多任务中，奖励函数不太好定义，比如自然语言中一个问题的两种回答怎么区分好坏，没有固定的定义规则。故大家会看到初期大语言模型会主动输出两个答案来让用户告诉他哪个答案好。本质上这个就是模型在初期也不知道哪种结果好，需要通过这种方式收集用户的反馈。通过用户反馈的结果，大语言模型会类似学习出一个reward-model。在主模型训练任务中，会通过reward-model来指导强化学习任务中的奖励信号。类似自然语言模型，自动驾驶中的reward，相对来说有一些比较明确的定义。但本身为了进一步衡量舒适性/效率等指标，会利用专家数据（高质量的人类驾驶数据）+ 不太好的驾驶行为数据共同训练出一个reward-model，因为强化学习是利用reward来指导模型训练，而上述描述的任务本身是为了学习生成reward，这个过程刚好相反，故一般把这些任务叫做逆强化学习。

强化学习相关的基础知识

马尔可夫（决策）过程

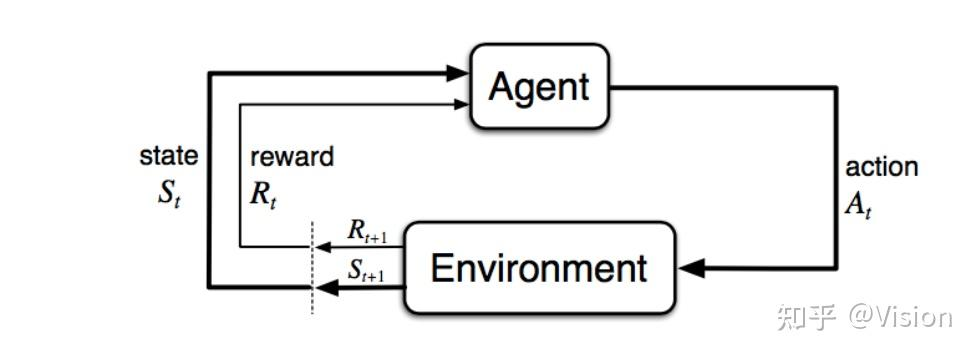
假设一个智能体在执行时序任务时，其动作本身可分解成系列状态概率转移任务，比如时间戳t下自己的状态（s）, 根据状态转移矩阵（p），以一定概率执行了动作（a），得到了缓解给的反馈（r），同时动作本身又对环境做出了改变（s'）。整个这样的时序过程就被称为马尔可夫决策过程。时序序列的长短都可以按任务本身给予设定。常见的自动驾驶任务中的目标生命周期管理/ hmm 状态估计等。

马尔可夫决策过程示意图

动态规划

一个任务本身可以分解为系列最优子问题的过程，就是一个动态规划解决的过程。比如背包问题等leetcode算法。在一些离散空间的任务中，很多时序任务就是一个动态规划问题。

蒙特卡洛方法

蒙特卡洛（mc）算法本质是利用一种大数原理（统计学）的方法来去解决问题。一般认为，当统计值大于一定的数量后，客观表现就能反应出模型本身的一些特性。类似利用最大后验概率来估计模型参数的一种方法。

强化学习的基本概念

• 策略（policy）：即智能体（譬如自动驾驶中的车辆）按照某种固定策略做出的一系列马尔可夫决策过程。本身这个策略就是自动驾驶任务中轨迹规划模型。根据策略的确定性，可分为下面两种，一般自动驾驶建模都是第一种，第二种一般在更复杂的模型中考虑，比如下雨天地面潮湿，执行action后并不是完全执行到固定一个状态。

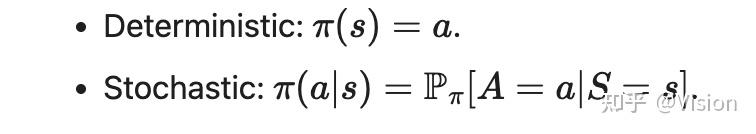
• 奖励（reward）：智能体每执行一个action达到某个状态，环境给予这个动作造成的状态的一个反馈。自动驾驶中的reward就是碰撞等类似的描述等。整体自动驾驶强化学习的目标是使得最终某个状态下的奖励期望最大。

• 价值回报（return）: 每个状态的reward时序期望值，一般的定义如下，gamma为衰减因子（<1）. 一方面方便数学无穷建模，另一个方面也体现当前的reward具备最大意义。

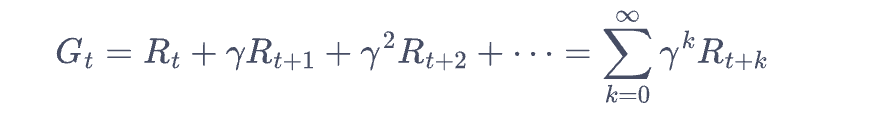
• 状态价值（函数）（V(s)）：一个状态的期望回报，强化学习的目标就是最大化这个目标

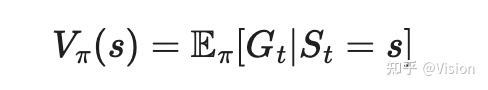
• 动作价值函数（Q(s,a)）: 一个状态和对应动作下的期望回报

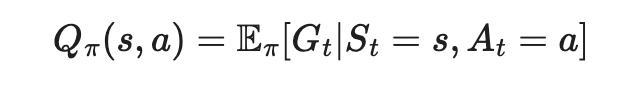
• 价值函数和动作价值的关系可以通过表达式简单推理出来

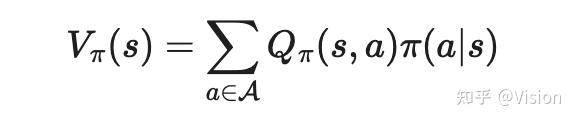
• 优势函数（A）: 具体就是动作价值函数与价值函数的差

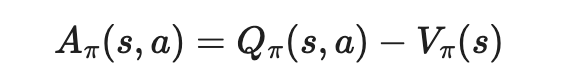
• 贝尔曼方程：一个关于价值函数的数学递推分解，就是一个动态规划过程

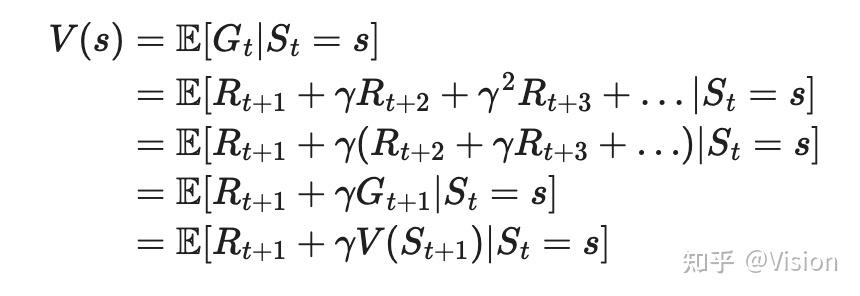
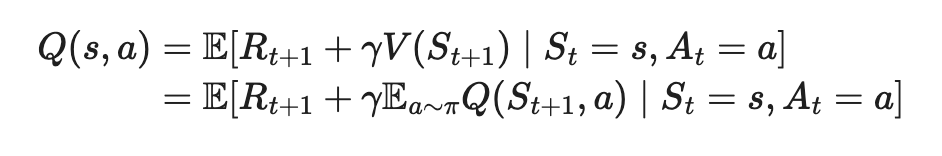
• 贝尔曼期望方程：针对一条具体的策略（pai），可能会生成多条（s，a）对，这些对的统计期望如下：

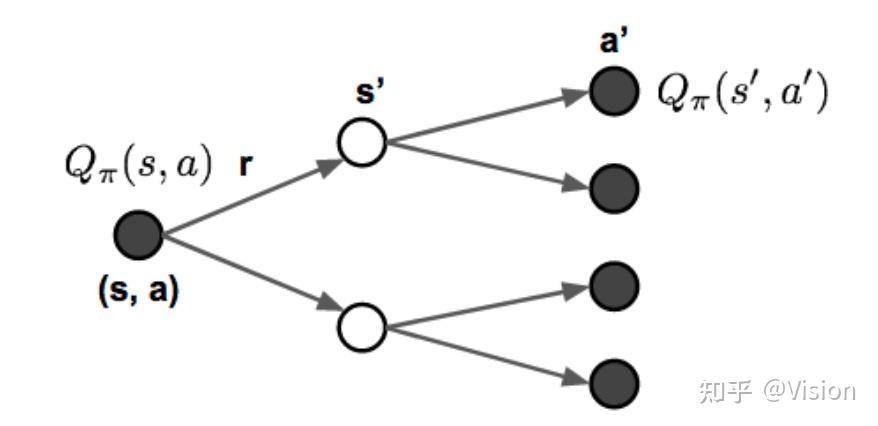
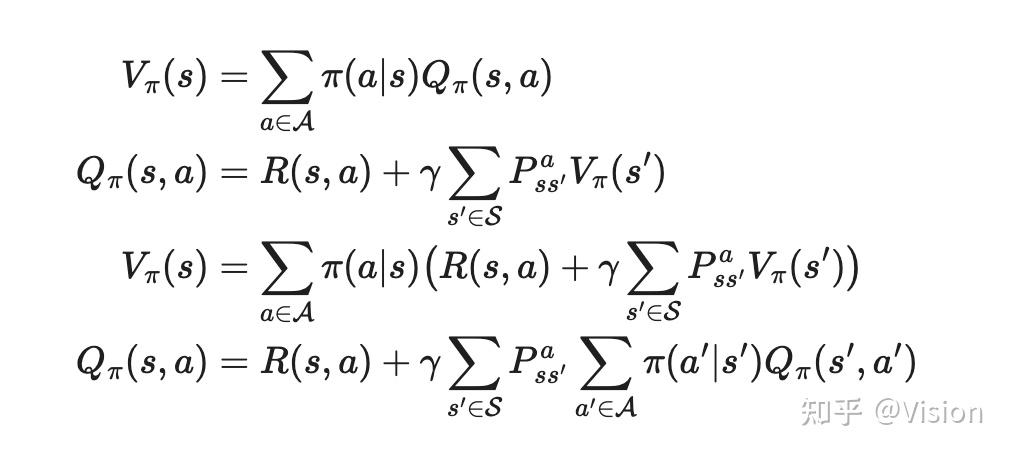
• 贝尔曼最优方程：通过最大化v或者q的过程来得到最优的v/q过程

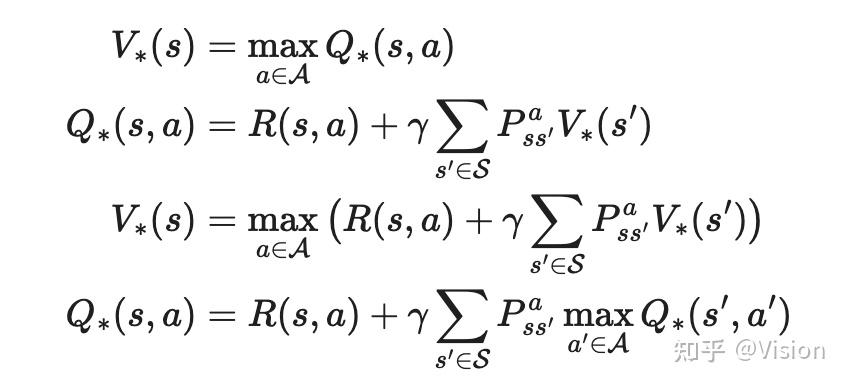
强化学习的基本分类标准

一般的任务空间，环境可能是已知的（比如围棋的棋盘格19* 19），但也可能是未知的（自动驾驶的轨迹规划任务）；动作也可能离散的（围棋上下左右走），也可能是连续的（轨迹走多少米）。故价值函数或者动作价值函数在连续空间建模的复杂度也比较高，通过直接建模优化价值函数的方法几乎不太可能，故有的方法是直接通过建模优化策略参数的方式达到最大化优化。

值优化

• 直接最大化q或者v函数的方法

• 常见算法：动态规划；; 蒙特卡洛算法；时序差分（td）算法（sarsa, q-learning）; mc+td结合（gae）

策略优化

• 通过优化策略参数的方式来最大化价值函数

• reinforce算法；a-c算法；trpo算法；ppo算法；

on-policy在线算法(model_base)

• 算法必须依赖实时策略生成，但每次策略生成后环境数据都已经发生变化，故数据无法重新生成。一般来说整体训练稳定性会差一些。

off-policy离线算法（model-free）

• 即训练数据可以从数据集中多次利用，跟动态策略生成环境关系不大。训练稳定性好，但跟真实策略分布有偏差。

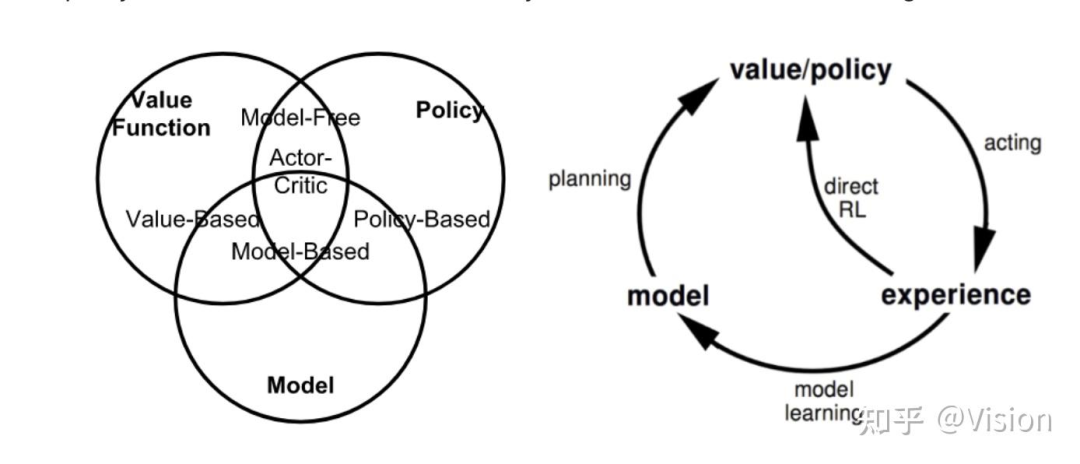
强化学习的基本算法

动态规划算法

这里一般会对离散任务进行动态规划求解，叫做策略迭代算法。过程一般分两步，一个是策略评估，一个是策略提升。策略评估过程主要为最开始智能体对环境不太熟悉，只能通过不断的环境交互采集多次行为，通过行为反馈来不断收敛完善目前的策略，即q/v函数。

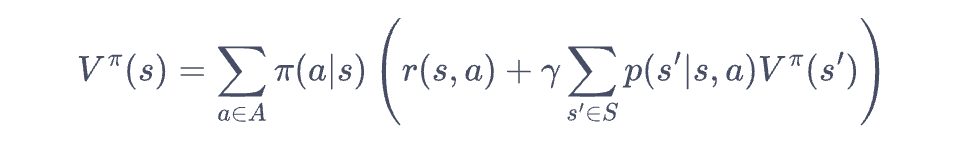
当策略估计出来了，为了最大化奖励函数，故采取贪婪算法来使得增加v/a函数。

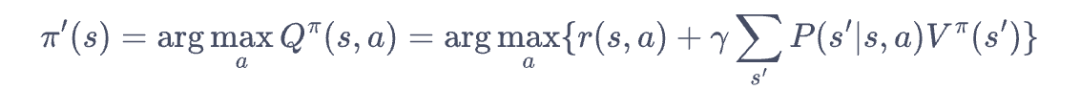
但实际上策略评估过程比较耗时，可以采取一步评估+一次迭代的方式来加速求解过程，这个过程就被称为价值迭代算法

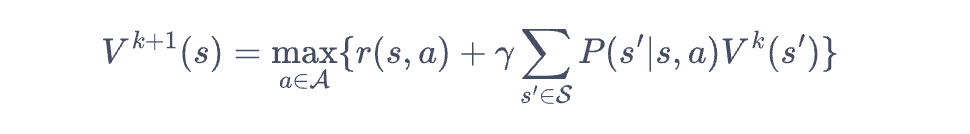
蒙塔卡洛方法

简单点，就是所有状态动作系列的统计平均。

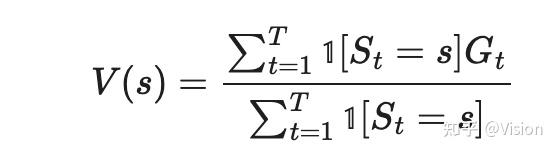
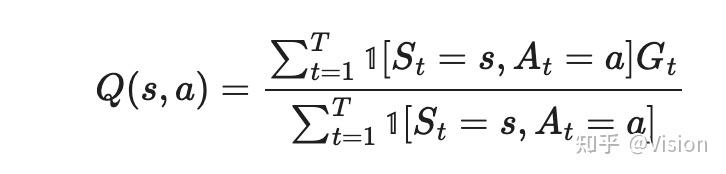
时序差分算法

类似mc方法中的价值更新方法，可以将1/n(s)简化成一个常数alpha；

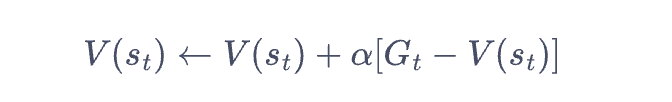
根据价值函数的公式，可推导出价值函数和reward之间的关系

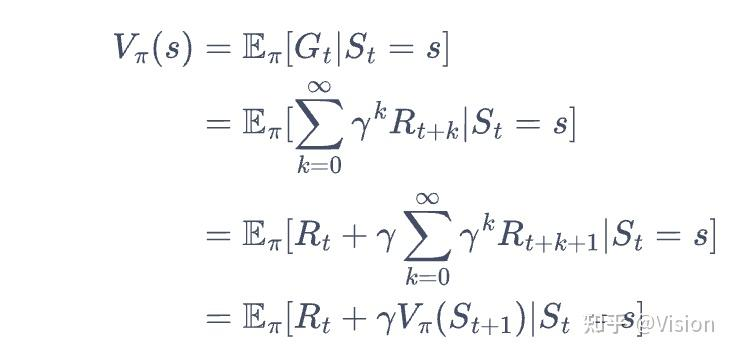
可以进一步得到v（s_t）和 v(s_t+1)的更新关系：

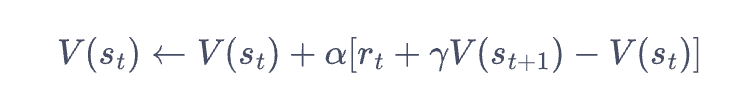
故得到定义（后面常用的）：

• 时序差分目标： r_t + gamma* v(s_t+1)

• 时序差分误差：r_t + gamma* v(s_t+1) - v(s_t).

根据这个派生出来的算法：

• SARSA: On-Policy TD control：

• 多步saras算法：即将单步差分变为有限多步，这样可以减少单步近似导致的偏差。

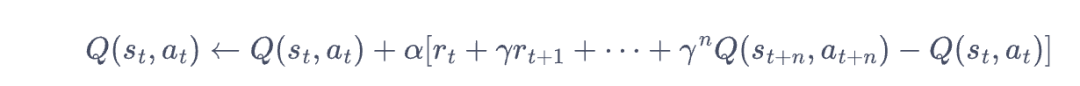
• Q-Learning: Off-policy TD control： 相对于sarsa算法，就看a'的数据是不需要的，所以不需要一定是on-line的数据训练，训练效率会更高。

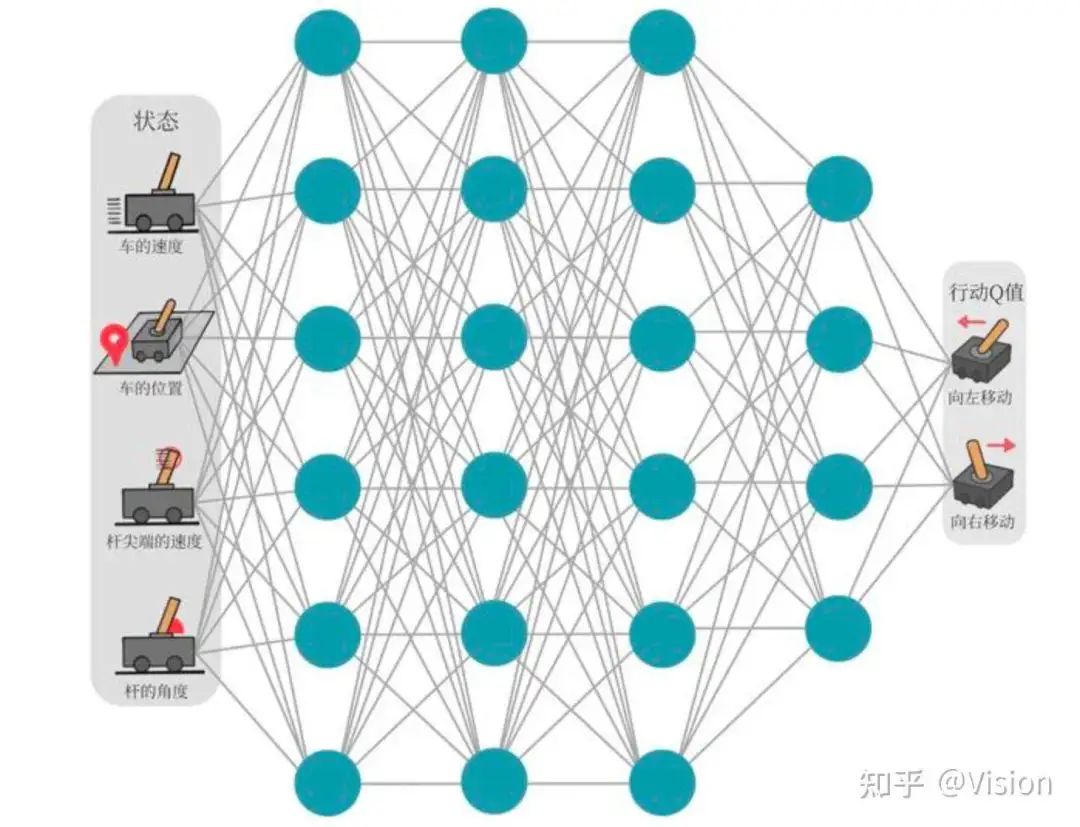
• dqn算法：

对于连续的状态表达，基本无法枚举表格来表达q/v，故可直接利用网络参数来表达。故本身就是学习一堆参数表达的q。但一般参数比较大的情况下，想要去学习一个比较好的q，是比较困难的。所以提出了两个策略方法：数据经验回放（类似off-model方法，在线收集数据用于多次训练） + 目标网络（利用一个相对时间内稳定的参数作为学习的目标，避免大范围震荡）

• 后续则针对dqn也有一些改进算法，比如double dqn，针对dqn方法出现的累计误差，更新获取价值函数action的方法（利用比较新的策略网络）：

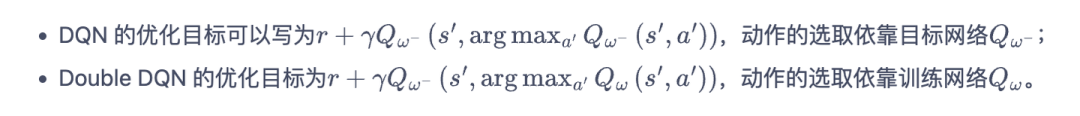
Dueling DQN针对直接学习价值网络，改为学习q + a的和，同时增加一个a的正则项。

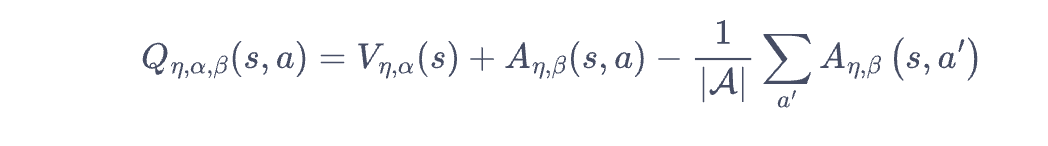
• gae（广义优势估计）算法：mc + td混合方法

通过时序差分计算advanage时，由于是单步会最终估计结果存在一定偏差。为了更加全面，引入了一种优势函数的估计算法，通过（1-lamada）的系数累计多步时序差分值的和作为最终的优势估计。

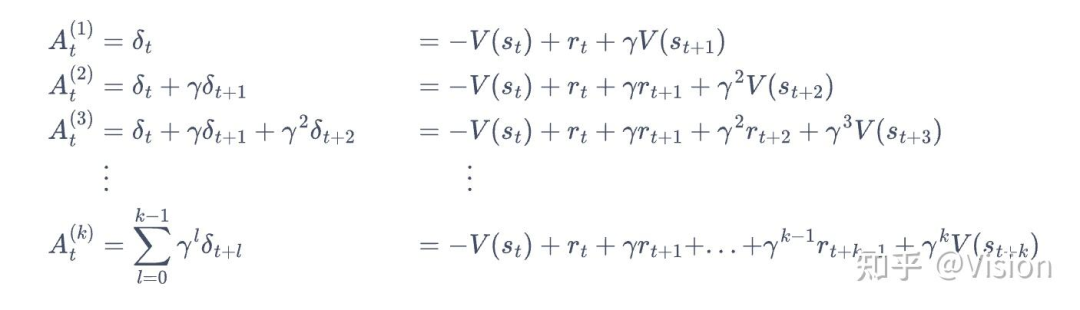
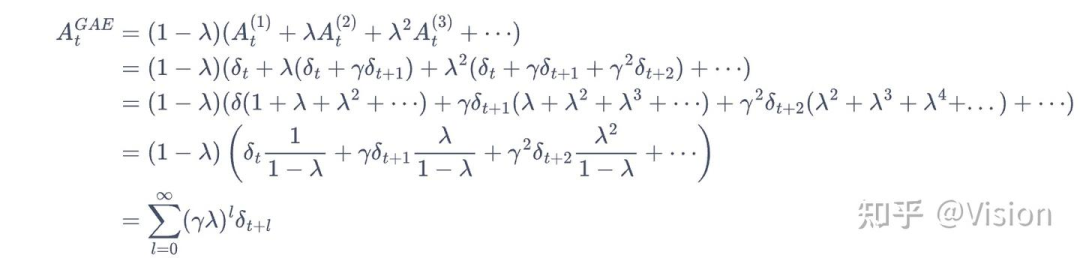
策略梯度算法

前面的方法都是直接用于价值函数，但可以通过去策略梯度求导的方式来更新算法。

定义目标函数：即最大化价值函数。

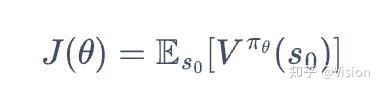
对该函数求导，数学推导后得：这个数学公式很重要，决定了后续的策略算法推理的基础，推导比较复杂。

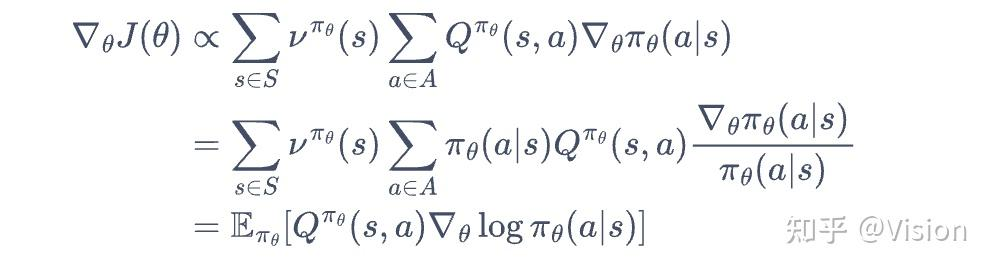
REINFORCE 算法： 是采用了蒙特卡洛方法来估计策略梯度中的q

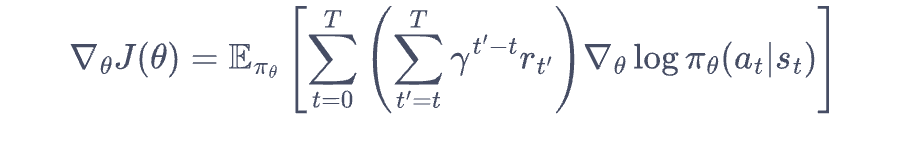
G = 0
        self.optimizer.zero_grad()
        for i in reversed(range(len(reward_list))):  # 从最后一步算起
            reward = reward_list[i]
            state = torch.tensor([state_list[i]],
                                 dtype=torch.float).to(self.device)
            action = torch.tensor([action_list[i]]).view(-1, 1).to(self.device)
            log_prob = torch.log(self.policy_net(state).gather(1, action))
            G = self.gamma * G + reward
            loss = -log_prob * G  # 每一步的损失函数
            loss.backward()  # 反向传播计算梯度
        self.optimizer.step()  # 梯度下降

• actor-critic算法：将策略梯度中的q，利用一个值函数来拟合（深度学习网络），即在策略学习的同学，也引入直接q值学习的方法，但本质上还是一个策略梯度算法。实际上有paper证明这个q可以扩展为多种写法表达形式

def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'],
                              dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
            self.device)
        rewards = torch.tensor(transition_dict['rewards'],
                               dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'],
                                   dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'],
                             dtype=torch.float).view(-1, 1).to(self.device)

        # 时序差分目标
        td_target = rewards + self.gamma * self.critic(next_states) * (1 -
                                                                       dones)
        td_delta = td_target - self.critic(states)  # 时序差分误差
        log_probs = torch.log(self.actor(states).gather(1, actions))
        actor_loss = torch.mean(-log_probs * td_delta.detach())
        # 均方误差损失函数
        critic_loss = torch.mean(
            F.mse_loss(self.critic(states), td_target.detach()))
        self.actor_optimizer.zero_grad()
        self.critic_optimizer.zero_grad()
        actor_loss.backward()  # 计算策略网络的梯度
        critic_loss.backward()  # 计算价值网络的梯度
        self.actor_optimizer.step()  # 更新策略网络的参数
        self.critic_optimizer.step()  # 更新价值网络的参数

• trpo（trust region policy optimization）: 为了保证训练的稳定性，引入参考重要性采样比例，引入置信区间。但整体由于约束条件的存在，整体计算会比较复杂，包括泰勒最优近似/共轭梯度计算/线性查找等步骤。策略网络更新代码如下，价值网络仍然为a-c算法的学习参数。

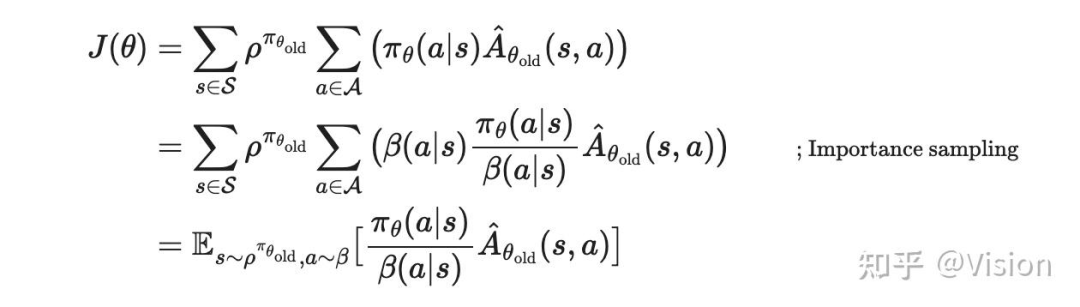
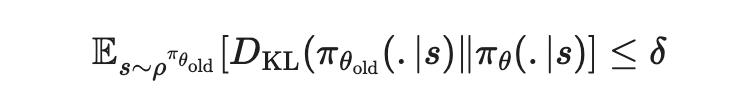
def policy_learn(self, states, actions, old_action_dists, old_log_probs,
                     advantage):  # 更新策略函数
        surrogate_obj = self.compute_surrogate_obj(states, actions, advantage,
                                                   old_log_probs, self.actor)
        grads = torch.autograd.grad(surrogate_obj, self.actor.parameters())
        obj_grad = torch.cat([grad.view(-1) for grad in grads]).detach()
        # 用共轭梯度法计算x = H^(-1)g
        descent_direction = self.conjugate_gradient(obj_grad, states,
                                                    old_action_dists)

        Hd = self.hessian_matrix_vector_product(states, old_action_dists,
                                                descent_direction)
        max_coef = torch.sqrt(2 * self.kl_constraint /
                              (torch.dot(descent_direction, Hd) + 1e-8))
        new_para = self.line_search(states, actions, advantage, old_log_probs,
                                    old_action_dists,
                                    descent_direction * max_coef)  # 线性搜索
        torch.nn.utils.convert_parameters.vector_to_parameters(
            new_para, self.actor.parameters())  # 用线性搜索后的参数更新策略

• ppo（proximal policy optimization）算法：简化trpo约束条件的求解，将约束条件变成了一个clip函数。策略网络更新代码如下，价值网络仍然为a-c算法的学习参数。

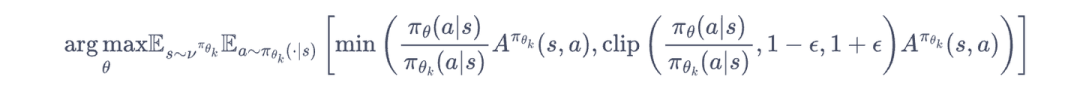
def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'],
                              dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
            self.device)
        rewards = torch.tensor(transition_dict['rewards'],
                               dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'],
                                   dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'],
                             dtype=torch.float).view(-1, 1).to(self.device)
        td_target = rewards + self.gamma * self.critic(next_states) * (1 -
                                                                       dones)
        td_delta = td_target - self.critic(states)
        advantage = rl_utils.compute_advantage(self.gamma, self.lmbda,
                                               td_delta.cpu()).to(self.device)
        old_log_probs = torch.log(self.actor(states).gather(1,
                                                            actions)).detach()

        for _ in range(self.epochs):
            log_probs = torch.log(self.actor(states).gather(1, actions))
            ratio = torch.exp(log_probs - old_log_probs)
            surr1 = ratio * advantage
            surr2 = torch.clamp(ratio, 1 - self.eps,
                                1 + self.eps) * advantage  # 截断
            actor_loss = torch.mean(-torch.min(surr1, surr2))  # PPO损失函数
            critic_loss = torch.mean(
                F.mse_loss(self.critic(states), td_target.detach()))
            self.actor_optimizer.zero_grad()
            self.critic_optimizer.zero_grad()
            actor_loss.backward()
            critic_loss.backward()
            self.actor_optimizer.step()
            self.critic_optimizer.step()

• grpo（group releative policy optimization）： deepseek提出的一种优化算法，利用在线group样本的统计平均的方法来替换value-model，让整个网络更轻量。另外还加了一个分布的熵函数约束和kl。

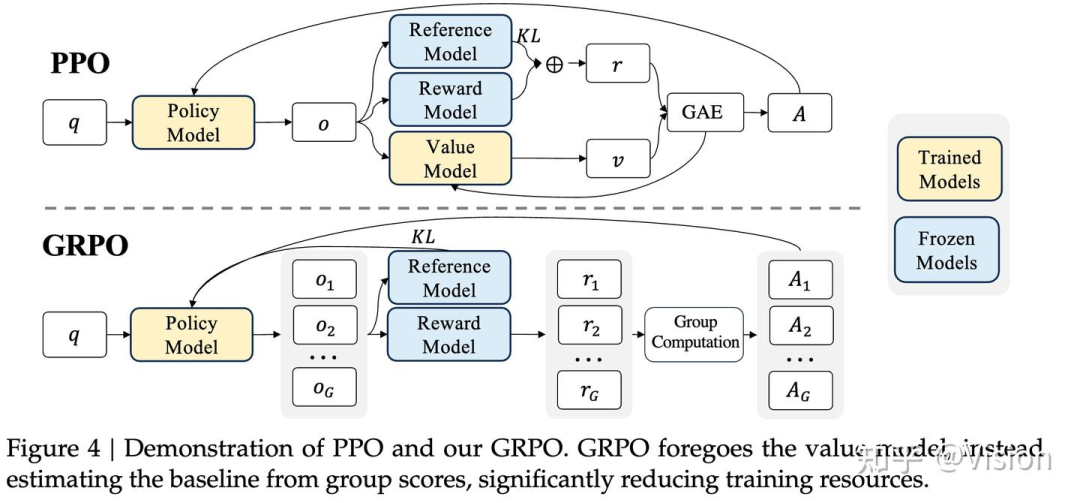
自动驾驶轨迹规划的强化学习

常见的模仿学习学出来的策略本身缺少因果的建模关系，比如车路口起步，是因为绿灯亮了，还是旁边的车启动了，还是人行道上没有行人，这些原因对于结果来说太过于复杂。即输入的特征空间特别大，导致输入与输出的对应关系建模困难。这时候就需要强化学习的思路来提升策略的因果性，而且可以通过正负样本的数据定义来设置不同的驾驶风格（高级功能）。自动驾驶里的强化学习轨迹规划任务更多是连续空间下的连续决策问题，来谈几个常用的关键点：

预训练：

为了训练任务更加稳定，一般会对策略网络和价值网络进行预训练，可以利用简单的模仿学习任务进行训练。

策略梯度中的概率建模

为了构建与环境的关系，可以利用一个可导的概率建模方法（自回归 / difusion/ 高斯采样等）来对action进行概率建模，然后多步rollout，通过环境reward反馈来学习整体策略。

reward设计

自动驾驶中的reward主要是安全性/安心感/效率等，这些都比较好规则定义实现。更高级一些的比如驾驶风格/舒适性等的rewerd，一般需要通过逆强化学习的思路来进行训练

闭环训练

主车进行一个action后，对环境的影响比较动态（他车大概率会响应主车的动作，就是俗称说的动态博弈），那如何准确描述这个环境需要其他车的运动模型建模（这个就是多智能体博弈），这个需要在一个闭环仿真系统里实现。一般工程上会做驾驶，即他车的运动是不受主车运动影响，但这种训练出来的主车驾驶行为一般比较弱。

端到端+ 强化学习

主车闭环训练中，如果主车行为变了，环境也会跟着变化（比如摄像头看到的视角），这个时候需要实时生成更新后的sensor内容，这里就会需要系列图像生成的方法，比如传统的光线追踪/nerf/3d gs/ world model等。

总结

强化学习算法的后期技术理论发展迅猛，一些比如提升训练稳定性的方法陆续被提出，但经典的思路无外乎策略梯度或者直接值优化两种大的方法。对理论公式比较反感的同学，建议多动手写写代码，相信大家能很快入手强化学习！

自动驾驶之心

论文辅导来啦

自驾交流群来啦！

自动驾驶之心创建了近百个技术交流群，涉及大模型、VLA、端到端、数据闭环、自动标注、BEV、Occupancy、多模态融合感知、传感器标定、3DGS、世界模型、在线地图、轨迹预测、规划控制等方向！欢迎添加小助理微信邀请进群。

知识星球交流社区

近4000人的交流社区，近300+自动驾驶公司与科研结构加入！涉及30+自动驾驶技术栈学习路线，从0到一带你入门自动驾驶感知（大模型、端到端自动驾驶、世界模型、仿真闭环、3D检测、车道线、BEV感知、Occupancy、多传感器融合、多传感器标定、目标跟踪）、自动驾驶定位建图（SLAM、高精地图、局部在线地图）、自动驾驶规划控制/轨迹预测等领域技术方案、大模型，更有行业动态和岗位发布！欢迎加入。

独家专业课程

端到端自动驾驶、大模型、VLA、仿真测试、自动驾驶C++、BEV感知、BEV模型部署、BEV目标跟踪、毫米波雷达视觉融合、多传感器标定、多传感器融合、多模态3D目标检测、车道线检测、轨迹预测、在线高精地图、世界模型、点云3D目标检测、目标跟踪、Occupancy、CUDA与TensorRT模型部署、大模型与自动驾驶、NeRF、语义分割、自动驾驶仿真、传感器部署、决策规划、轨迹预测等多个方向学习视频

学习官网：www.zdjszx.com