作者 | 萌萌的糖 编辑 | 汽车人
原文链接:https://zhuanlan.zhihu.com/p/657147115
点击下方卡片,关注“自动驾驶之心”公众号
ADAS巨卷干货,即可获取
点击进入→自动驾驶之心【车道线检测】技术交流群
本文只做学术分享,如有侵权,联系删文
1 开篇
我们已经对感知组件有了比较清晰的认识。从这篇文章开始,如果有大佬已经讲过某组件整体的运行逻辑,我将不会再重复该部分工作,而是分析那些还没有被提及的细节和难点,相信大家更有耐心看下去。
所以,本文的重点落在了车道线后处理上。
首先我们在lane_camera_perception.cc文件中的LaneCameraPerception::Perception()方法可以发现整个车道线的检测的流程为:
调用DarkSCNN进行车道线分割;
分割结果2D后处理;
相机在线标定,计算相机高度和pitch角度;
3D后处理。
// DarkSCNN进行车道线分割
if (!lane_detector_->Detect(lane_detetor_options, frame)) {
AERROR << "Failed to detect lane.";
return false;}
PERF_BLOCK_END_WITH_INDICATOR(frame->data_provider->sensor_name(),
"LaneDetector");
// 分割结果2D后处理
if (!lane_postprocessor_->Process2D(lane_postprocessor_options, frame)) {
AERROR << "Failed to postprocess lane 2D.";
return false;
}
PERF_BLOCK_END_WITH_INDICATOR(frame->data_provider->sensor_name(),
"LanePostprocessor2D");
// 根据当前帧检测出的车道线求取相机高度和pitch角
frame->calibration_service->Update(frame);
PERF_BLOCK_END_WITH_INDICATOR(frame->data_provider->sensor_name(), "CalibrationService");
// 3D后处理
if (!lane_postprocessor_->Process3D(lane_postprocessor_options, frame)) {
AERROR << "Failed to postprocess lane 3D.";
return false;
}
PERF_BLOCK_END_WITH_INDICATOR(frame->data_provider->sensor_name(),
"LanePostprocessor3D");本篇文章注重分析车道线拟合代码,主要包含以下3部分:
2D车道线拟合代码分析;
相机在线标定代码分析;
3D车道线拟合代码分析。
2 2D车道线拟合
Apollo采用DarkSCNN算法完成一共13条车道线语义分割,神经网络的输出结果包含两部分:1.13条车道分割结果;2.灭点检测结果,具体参考Frank,对于车道线分割输出结果,每条车道线都是单独一个通道,这样的设计也方便车道线的后处理。当车道线检测完成后会调用DarkSCNNLanePostprocessor::Process2D()方法进行2D车道线拟合。其总体流程如下:
2.1 车道线下采样
bool DarkSCNNLanePostprocessor::Process2D(const LanePostprocessorOptions& options, CameraFrame* frame)
{
ADEBUG << "Begin to Process2D.";
frame->lane_objects.clear();
auto start = std::chrono::high_resolution_clock::now();
cv::Mat lane_map(lane_map_height_, lane_map_width_, CV_32FC1);
// copy data
memcpy(lane_map.data, frame->lane_detected_blob->cpu_data(),
lane_map_width_ * lane_map_height_ * sizeof(float));
int y = static_cast<int>(lane_map.rows * 0.9 - 1); // 480 * 0.9 - 1 = 431
// step_y为采样步长,动态变化
// y = y - step_y
// 越挨着图片底部,越有可能是车道区域,步长越小,
int step_y = (y - 40) * (y - 40) / 6400 + 1; // step_y = 25,实际上并没有用这个
xy_points.clear();
xy_points.resize(lane_type_num_);
uv_points.clear();
uv_points.resize(lane_type_num_);
// 分割结果采样
while (y > 0) {
for (int x = 1; x < lane_map.cols - 1; ++x) {
int value = static_cast<int>(round(lane_map.at<float>(y, x)));
// lane on left(自车左车道)
if ((value > 0 && value < 5) || value == 11) {
// right edge (inner) of the lane
if (value != static_cast<int>(round(lane_map.at<float>(y, x + 1)))) {
// 车道线在图像上坐标
Eigen::Matrix<float, 3, 1> img_point(static_cast<float>(x * roi_width_ / lane_map.cols),
static_cast<float>(y * roi_height_ / lane_map.rows + roi_start_),
1.0);
Eigen::Matrix<float, 3, 1> xy_p;
// trans_mat_为单应矩阵:表示图像上车道平面投影到车辆坐标系下的投影矩阵?
// trans_mat_的计算感觉有点问题
xy_p = trans_mat_ * img_point; // 车辆坐标系下的点
Eigen::Matrix<float, 2, 1> xy_point;
Eigen::Matrix<float, 2, 1> uv_point;
if (std::fabs(xy_p(2)) < 1e-6)
continue;
// 归一化坐标
xy_point << xy_p(0) / xy_p(2), xy_p(1) / xy_p(2);
// Filter out lane line points
if (xy_point(0) < 0.0 || // This condition is only for front camera
xy_point(0) > max_longitudinal_distance_ || std::abs(xy_point(1)) > 30.0) {
continue;
}
// 保存两者的坐标点
uv_point << static_cast<float>(x * roi_width_ / lane_map.cols),
static_cast<float>(y * roi_height_ / lane_map.rows + roi_start_);
if (xy_points[value].size() < minNumPoints_ || xy_point(0) < 50.0f || std::fabs(xy_point(1) - xy_points[value].back()(1)) < 1.0f) {
xy_points[value].push_back(xy_point);
uv_points[value].push_back(uv_point);
}
}
} else if (value >= 5 && value < lane_type_num_) {
// Left edge (inner) of the lane
...
...
}
}
// 实际采用这里的step_y
step_y = (y - 45) * (y - 45) / 6400 + 1; // 30
y -= step_y;
}
}进入Process2D方法,首先获取车道线分割结果的Blob,然后对车道线进行非均匀采样。然后将图片上的车道线坐标进行投影。不太确定的是,这里的投影矩阵trans_mat_是图片坐标系到车辆坐标系的投影矩阵?将图片上的车道线坐标通过单应性矩阵投影到车辆归一化平面???经过分析对应的trans_mat_设置流程如下:
Visualizer::Init_all_info_single_camera()->Visualizer::adjust_angles()->DarkSCNNLanePostprocessor::SetIm2CarHomography()2.2 单应矩阵求解
其主要调用Visualizer::adjust_angles()方法求取单应矩阵,代码如下:
bool Visualizer::adjust_angles(const std::string &camera_name,
const double pitch_adj_degree,
const double yaw_adj_degree,
const double roll_adj_degree) {
// Convert degree angles to radian angles
double pitch_adj_radian = pitch_adj_degree * degree_to_radian_factor_;
double yaw_adj_radian = yaw_adj_degree * degree_to_radian_factor_;
double roll_adj_radian = roll_adj_degree * degree_to_radian_factor_;
// We use "right handed ZYX" coordinate system for euler angles
// adjust pitch yaw roll in camera coords
// Remember that camera coordinate
// (Z)----> X
// |
// |
// V
// Y
Eigen::Matrix4d Rx; // pitch
Rx << 1, 0, 0, 0, 0, cos(pitch_adj_radian), -sin(pitch_adj_radian), 0, 0,
sin(pitch_adj_radian), cos(pitch_adj_radian), 0, 0, 0, 0, 1;
Eigen::Matrix4d Ry; // yaw
Ry << cos(yaw_adj_radian), 0, sin(yaw_adj_radian), 0, 0, 1, 0, 0,
-sin(yaw_adj_radian), 0, cos(yaw_adj_radian), 0, 0, 0, 0, 1;
Eigen::Matrix4d Rz; // roll
Rz << cos(roll_adj_radian), -sin(roll_adj_radian), 0, 0, sin(roll_adj_radian),
cos(roll_adj_radian), 0, 0, 0, 0, 1, 0, 0, 0, 0, 1;
// adjusted_camera2car_camera2car表示相机到车辆坐标系的位姿变换
adjusted_camera2car_ = ex_camera2car_ * Rz * Ry * Rx;
AWARN << "adjusted_camera2car_: " << adjusted_camera2car_;
// Get homography from projection matrix
// ====
// Version 1. Direct
// compute the homography matrix, such that [u, v, 1] ~ H [X_l, Y_l, 1]
Eigen::Matrix3d R = adjusted_camera2car_.block(0, 0, 3, 3); // 取出旋转矩阵 camera->car
Eigen::Vector3d T = adjusted_camera2car_.block(0, 3, 3, 1); // 取出平移向量 camera->car
Eigen::Matrix3d H; // 3*3
Eigen::Matrix3d H_inv;
// 直接展开计算得到 Rccamera_car
H.block(0, 0, 3, 2) = (K_[camera_name] * R.transpose()).block(0, 0, 3, 2); // 这里好理解
H.block(0, 2, 3, 1) = -K_[camera_name] * R.transpose() * T; // 为什么是这样的??
H_inv = H.inverse();
homography_ground2image_[camera_name] = H;
homography_image2ground_[camera_name] = H_inv;
// Version 2. Conceptual ##########################
// ex_car2camera_ = adjusted_camera2car_.inverse();
// // compute the homography matrix, such that H [u, v, 1]' ~ [X_l, Y_l, 1]
// Eigen::Matrix3d R = ex_car2camera_.block(0, 0, 3, 3);
// Eigen::Vector3d T = ex_car2camera_.block(0, 3, 3, 1);
// projection_matrix_.setIdentity();
// projection_matrix_.block(0, 0, 3, 3) = K_ * R;
// projection_matrix_.block(0, 3, 3, 1) = K_ * T;
// homography_ground2image_.block(0, 0, 3, 2)
// = projection_matrix_.block(0, 0, 3, 2);
// homography_ground2image_.block(0, 2, 3, 1)
// = projection_matrix_.block(0, 3, 3, 1);
// AINFO << "homography_ground2image_: ";
// AINFO << homography_ground2image_;
// homography_image2ground_ = homography_ground2image_.inverse();
return true;
}推导如下:设相机内参
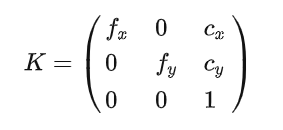
车辆坐标系到相机坐标系的旋转矩阵
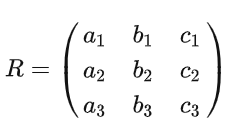
车辆坐标系到相机坐标系的平移向量
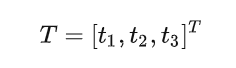
将车辆自身归一化坐标向图片投影
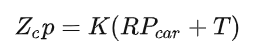
将内参和旋转矩阵带入该方程,展开如下
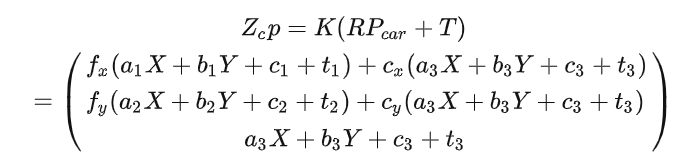

可到到单应矩阵
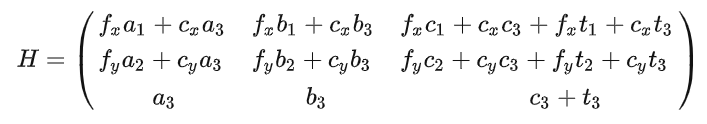
对应上面代码,发现单应矩阵最后一列H.block(0, 2, 3, 1) = -K_[camera_name] * R.transpose() * T;不太理解,是我推导错了吗??希望大佬指正!!!这里的单应矩阵是车辆坐标系的车道平面和图像坐标系上的车道平面的投影关系,并不是两张图片间的变换矩阵。参考:
2.3 2D车道线拟合
2D车道线拟合的思想是遍历所有下采样后车道线检测结果,每根车道线进行随机采样一致性算法(Ransac),得到车道线曲线方程。
// 2. Remove outliers and Do a ransac fitting
std::vector<Eigen::Matrix<float, 4, 1>> coeffs;
std::vector<Eigen::Matrix<float, 4, 1>> img_coeffs;
std::vector<Eigen::Matrix<float, 2, 1>> selected_xy_points;
coeffs.resize(lane_type_num_);
img_coeffs.resize(lane_type_num_);
// 遍历每条车道线在归一化坐标系拟合其曲线方程
for (int i = 1; i < lane_type_num_; ++i) {
coeffs[i] << 0, 0, 0, 0;
if (xy_points[i].size() < minNumPoints_) // minNumPoints_ = 8
continue;
Eigen::Matrix<float, 4, 1> coeff;
// Solve linear system to estimate polynomial coefficients
// 每根车道线进行随机采样一致性算法(Ransac),去除外点,得到曲线函数
if (RansacFitting<float>(xy_points[i], &selected_xy_points, &coeff, 200,
static_cast<int>(minNumPoints_), 0.1f)) {
coeffs[i] = coeff;
xy_points[i].clear();
xy_points[i] = selected_xy_points;
} else {
xy_points[i].clear();
}
}RansacFitting()为车道线曲线拟合,代码如下:
template <typename Dtype>
bool RansacFitting(const std::vector<Eigen::Matrix<Dtype, 2, 1>>& pos_vec,
std::vector<Eigen::Matrix<Dtype, 2, 1>>* selected_points,
Eigen::Matrix<Dtype, 4, 1>* coeff, const int max_iters = 100,
const int N = 5,const Dtype inlier_thres = static_cast<Dtype>(0.1)){
if (coeff == nullptr) {
AERROR << "The coefficient pointer is NULL.";
return false;
}
selected_points->clear();
// 将车道线按点数分成3段
int n = static_cast<int>(pos_vec.size());
int q1 = static_cast<int>(n / 4);
int q2 = static_cast<int>(n / 2);
int q3 = static_cast<int>(n * 3 / 4);
if (n < N) {
AERROR << "The number of points should be larger than the order. #points = "
<< pos_vec.size();
return false;
}
std::vector<int> index(3, 0);
int max_inliers = 0;
Dtype min_residual = std::numeric_limits<float>::max();
Dtype early_stop_ratio = 0.95f;
Dtype good_lane_ratio = 0.666f;
for (int j = 0; j < max_iters; ++j) {
// 在三段中,随机采样3个点,进行曲线拟合,3个点会不会太少
index[0] = std::rand() % q2; // 0~n/2中取点
index[1] = q2 + std::rand() % q1; // n/2~n3/4中取点
index[2] = q3 + std::rand() % q1; //n3/4~n中取点
// 曲线模型:y = a_0 + a_1*x + a_2*x^2
Eigen::Matrix<Dtype, 3, 3> matA;
matA << pos_vec[index[0]](0) * pos_vec[index[0]](0), pos_vec[index[0]](0),
1, pos_vec[index[1]](0) * pos_vec[index[1]](0), pos_vec[index[1]](0), 1,
pos_vec[index[2]](0) * pos_vec[index[2]](0), pos_vec[index[2]](0), 1;
Eigen::FullPivLU<Eigen::Matrix<Dtype, 3, 3>> mat(matA);
mat.setThreshold(1e-5f);
if (mat.rank() < 3) { // 方程无非零解
ADEBUG << "matA: " << matA;
ADEBUG << "Matrix is not full rank (3). The rank is: " << mat.rank();
continue;
}
// y值
Eigen::Matrix<Dtype, 3, 1> matB;
matB << pos_vec[index[0]](1), pos_vec[index[1]](1), pos_vec[index[2]](1);
// 直接求解,但会出现矩阵不可逆的情况,可以向matA对角线上加上阻尼因子,保证矩阵可逆,也可以用最小二乘
Eigen::Vector3f c = static_cast<Eigen::Matrix<Dtype, 3, 1>>(matA.inverse() * matB);
if (!(matA * c).isApprox(matB)) {
ADEBUG << "No solution.";
continue;
}
int num_inliers = 0; // 内点数
Dtype residual = 0; // 总误差
Dtype y = 0;
// 对于每一个模型,遍历所有点,求预测值,判断是否为内点并计算总误差
for (int i = 0; i < n; ++i) {
// 预测值
y = pos_vec[i](0) * pos_vec[i](0) * c(0) + pos_vec[i](0) * c(1) + c(2);
if (std::abs(y - pos_vec[i](1)) <= inlier_thres)
++num_inliers;
// 总体误差
residual += std::abs(y - pos_vec[i](1));
}
// 内点数量足够多或者误差足够小,保存车道线曲线参数
if (num_inliers > max_inliers || (num_inliers == max_inliers && residual < min_residual)) {
(*coeff)(3) = 0;
(*coeff)(2) = c(0);
(*coeff)(1) = c(1);
(*coeff)(0) = c(2);
max_inliers = num_inliers;
min_residual = residual;
}
// 95%以上都是内点时,算法已经收敛
if (max_inliers > early_stop_ratio * n)
break;
}
// 内点数太少时,认为拟合失败
if (static_cast<Dtype>(max_inliers) / n < good_lane_ratio)
return false;
// 用最后得到的模型内点标记
for (int i = 0; i < n; ++i) {
Dtype y = pos_vec[i](0) * pos_vec[i](0) * (*coeff)(2) + pos_vec[i](0) * (*coeff)(1) + (*coeff)(0);
// 判断是否为内点
if (std::abs(y - pos_vec[i](1)) <= inlier_thres) {
selected_points->push_back(pos_vec[i]);
}
}
return true;
}假设车道线曲线方程
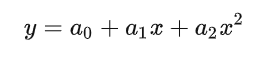
将车道线按点数分成3段,在三段中,随机采样3个点,若这三个点都满足曲线方程,则有
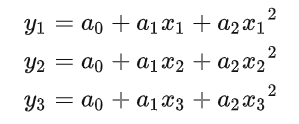
解法1:
写成矩阵形式有
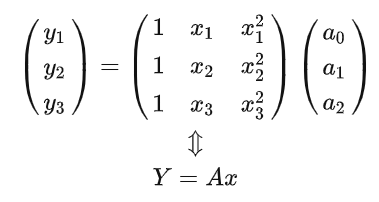
显然,如果矩阵A可逆
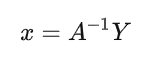
同样这里也可以采样4个点 或5个点,用QR分解求解其系数。
解法2:
令
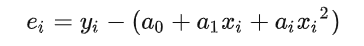
构建目标函数
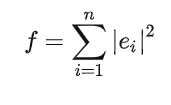
利用梯度下降、高斯-牛顿法或者Levenberg-Marquardt(LM)法求解得到系数
在Apollo中代码中采用的是方法一,但是加上了Ransac去除外点。至此第一部分内容已经介绍完了,总的来说还算简单,车道线合并请参考Frank的文章
3 相机在线标定
3.1 总体流程
相机标定的流程为:
加载自身车道的左右两车道线的点
根据定位计算当前帧与前一帧相机的位移和转角,并得到速度和角速度
通过转角判断相机是否直线运动,必须直线运动才能估计相机pitch角
通过检测到的车道线进行灭点估计
用估计的灭点计算相机pitch
pitch角直方滤波
值得注意的是整个过程中并没有相机高度的修正,在代码中也是直接采用默认高度。
这部分内容主要为通过已经检测出的2D车道线计算相机的pitch角和高度。在车道线检测组件中调用的接口为OnlineCalibrationService::Update(CameraFrame* frame),在该函数内部,其核心函数为calibrator_成员的Calibrate()的成员函数。
bool LaneLineCalibrator::Calibrate(const CalibratorOptions& options, float* pitch_angle)
{
if (pitch_angle == nullptr) {
AERROR << "pitch_angle is not available";
return false;
}
EgoLane ego_lane;
// 1.加载自车道和左右车道上的点,注意必须是左右两车道线都存在才返回true
if (!LoadEgoLaneline(*options.lane_objects, &ego_lane)) {
AINFO << "Failed to get the ego lane.";
return false;
}
// cam_ori为相机坐标原点
double cam_ori[4] = { 0 };
cam_ori[3] = 1.0;
// Camera to world pose
// Twc来自于定位channel
Eigen::Affine3d c2w = *options.camera2world_pose;
double p2w[12] = {c2w(0, 0),c2w(0, 1),c2w(0, 2),c2w(0, 3),c2w(1, 0),c2w(1, 1),c2w(1, 2),c2w(1, 3),
c2w(2, 0),c2w(2, 1),c2w(2, 2),c2w(2, 3),};
ADEBUG << "c2w transform this frame:\n"
<< p2w[0] << ", " << p2w[1] << ", " << p2w[2] << ", " << p2w[3] << "\n"
<< p2w[4] << ", " << p2w[5] << ", " << p2w[6] << ", " << p2w[7] << "\n"
<< p2w[8] << ", " << p2w[9] << ", " << p2w[10] << ", " << p2w[11];
// cam_coord_cur_ 为相机坐标系的原点在世界坐标系下的投影
common::IMultAx3x4(p2w, cam_ori, cam_coord_cur_);
time_diff_ = kTimeDiffDefault; // 默认时间差 1/15 15表示15FPS
yaw_rate_ = kYawRateDefault; // 角速度 0
velocity_ = kVelocityDefault; // 速度 8.333
timestamp_cur_ = *options.timestamp;
if (!is_first_frame_) {
time_diff_ = fabsf(static_cast<float>(timestamp_cur_ - timestamp_pre_));
ADEBUG << timestamp_cur_ << " " << timestamp_pre_ << std::endl;
// 2.根据当前时刻 、上一时刻,上上时刻相机在世界坐标系的魏位置,计算相机获取角速度和速度
camera::GetYawVelocityInfo(time_diff_, cam_coord_cur_, cam_coord_pre_, cam_coord_pre_pre_, &yaw_rate_, &velocity_);
std::string timediff_yawrate_velocity_text = absl::StrCat("time_diff_: ", std::to_string(time_diff_).substr(0, 4),
" | yaw_rate_: ", std::to_string(yaw_rate_).substr(0, 4),
" | velocity_: ", std::to_string(velocity_).substr(0, 4));
ADEBUG << timediff_yawrate_velocity_text << std::endl;
}
// 输入,左右车道线坐标,速度,角速度和时间间隔
bool updated = calibrator_.Process(ego_lane, velocity_, yaw_rate_, time_diff_);
if (updated) {
*pitch_angle = calibrator_.get_pitch_estimation();
float vanishing_row = calibrator_.get_vanishing_row();
AINFO << "#updated pitch angle: " << *pitch_angle;
AINFO << "#vanishing row: " << vanishing_row;
}
if (!is_first_frame_) {
memcpy(cam_coord_pre_pre_, cam_coord_pre_, sizeof(double) * 3);
}
is_first_frame_ = false;
memcpy(cam_coord_pre_, cam_coord_cur_, sizeof(double) * 3);
timestamp_pre_ = timestamp_cur_;
return updated;
}上面的代码已经完成了两步:LoadEgoLaneline(*options.lane_objects, &ego_lane)函数为加载左右两车道线的点,camera::GetYawVelocityInfo()为根据定位计算当前帧速度和角速度,这两部分代码相对简单,这里不再一一介绍。我们直接进入calibrator_.Process(ego_lane, velocity_, yaw_rate_, time_diff_)
bool LaneBasedCalibrator::Process(const EgoLane& lane, const float& velocity,const float& yaw_rate,
const float& time_diff){
// 根据时间计算位移和转角
float distance_traveled_in_meter = velocity * time_diff;
float vehicle_yaw_changed = yaw_rate * time_diff;
// 3.只有直线运动才能标定,转角超过3°认为不是直线运动
if (!IsTravelingStraight(vehicle_yaw_changed)) {
AINFO << "Do not calibate if not moving straight: "
<< "yaw angle changed " << vehicle_yaw_changed;
vp_buffer_.clear();
return false;
}
VanishingPoint vp_cur;
VanishingPoint vp_work;
// Get the current estimation on vanishing point from lane
// 4.灭点估计?为什么不用神经网络输出结果??
if (!GetVanishingPoint(lane, &vp_cur)) {
AINFO << "Lane is not valid for calibration.";
return false;
}
vp_cur.distance_traveled = distance_traveled_in_meter;
// std::cout << "#current v-row: " << vp_cur.pixel_pos[1] << std::endl;
// Push vanishing point into buffer
PushVanishingPoint(vp_cur);
if (!PopVanishingPoint(&vp_work)) {
AINFO << "Driving distance is not long enough";
return false;
}
// Get current estimation on pitch
// 5.pitch角度估计
pitch_cur_ = 0.0f;
if (!GetPitchFromVanishingPoint(vp_work, &pitch_cur_)) {
AINFO << "Failed to estimate pitch from vanishing point.";
return false;
}
vanishing_row_ = vp_work.pixel_pos[1];
// Get the filtered output using histogram
// 6.加入直方图,并进行滤波
if (!AddPitchToHistogram(pitch_cur_)) {
AINFO << "Calculated pitch is out-of-range.";
return false;
}
accumulated_straight_driving_in_meter_ += distance_traveled_in_meter;
// std::cout << "acc_d: " << accumulated_straight_driving_in_meter_ << "\n";
if (accumulated_straight_driving_in_meter_ > params_.min_distance_to_update_calibration_in_meter && pitch_histogram_.Process()) {
pitch_estimation_ = pitch_histogram_.get_val_estimation();
const float cy = k_mat_[5];
const float fy = k_mat_[4];
vanishing_row_ = tanf(pitch_estimation_) * fy + cy;
accumulated_straight_driving_in_meter_ = 0.0f;
return true;
}
return false;
}3.2 灭点计算
直线运动的判断仅仅通过转角判断。接着进行灭点计算,这里的灭点要求比较严格认为是两条世界坐标系平行直线的在图像上的交点,所以前面必须保证车辆是直线运动。灭点计算首先采样得到左右车道线的起始端点,再计算两条线段所在直线的端点。灭点计算整个流程如下:
bool LaneBasedCalibrator::GetVanishingPoint(const EgoLane& lane, VanishingPoint* v_point)
{
assert(v_point != nullptr);
float line_seg_l[4] = { 0 };
float line_seg_r[4] = { 0 };
// Get line segment
// 通过采样得到车道线线段端点坐标,左车道
bool get_line_seg_left = SelectTwoPointsFromLineForVanishingPoint(lane.left_line, line_seg_l);
if (!get_line_seg_left) {
AINFO << "Left lane is too short.";
return false;
}
// 通过采样得到车道线线段端点坐标 右车道
bool get_line_seg_right = SelectTwoPointsFromLineForVanishingPoint(lane.right_line, line_seg_r);
if (!get_line_seg_right) {
AINFO << "Right lane is too short.";
return false;
}
// Get vanishing point by line segments intersection
// 向量形式计算两个线段交点
return GetIntersectionFromTwoLineSegments(line_seg_l, line_seg_r, v_point);
}Apollo中采用的是向量法求取直线的交点,重点就是直线的向量表达即参数方程,具体代码内中给出的参考
3.3 pitrh角计算
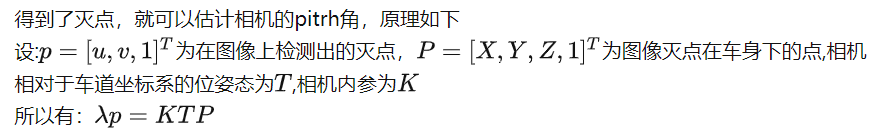
将其展开
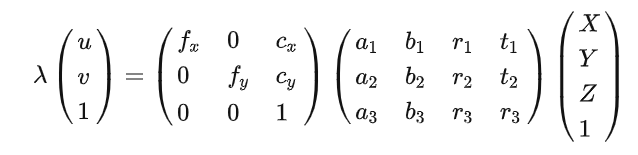

整理可得
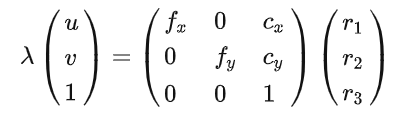
将其展开可得:
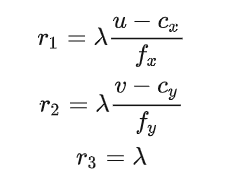
我们发现位姿变换T只剩下了第三列,我们知道欧拉角与旋转矩阵的关系参考:

根据欧拉角转换为旋转矩阵的公式:
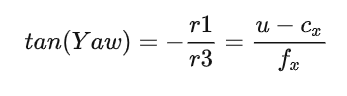

所以可以近似得到
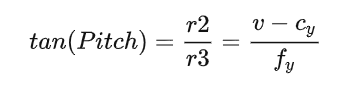
实现代码如下:
bool LaneBasedCalibrator::GetPitchFromVanishingPoint(const VanishingPoint& vp, float* pitch) const
{
assert(pitch != nullptr);
const float cx = k_mat_[2];
const float cy = k_mat_[5];
const float fx = k_mat_[0];
const float fy = k_mat_[4];
float yaw_check = static_cast<float>(atan2(vp.pixel_pos[0] - cx, fx));
// 车辆为直线运动,yaw角为约等于0
if (fabs(yaw_check) > params_.max_allowed_yaw_angle_in_radian) {
return false;
}
//pitch角计算
*pitch = static_cast<float>(atan2(vp.pixel_pos[1] - cy, fy));
return true;
}pitch计算完毕后,会进行直方图滤波,具体参考bool HistogramEstimator::Process()函数,这里不再过多叙述。至此,pitch角的计算已经分析完毕。
4 车道线3D处理
3D处理主要是将检测到的2D车道线坐标点,投影到相机坐标系下,然后在相机坐标系下进行3D车道线拟合,具体的接口如下:
bool DarkSCNNLanePostprocessor::Process3D(const LanePostprocessorOptions& options, CameraFrame* frame)
{
ConvertImagePoint2Camera(frame);
PolyFitCameraLaneline(frame);
return true;
}首先调用ConvertImagePoint2Camera(frame)将图像上的车道线点投影到相机归一化平面上,再根据前面计算出的相机pitch角修正该点的坐标,然后根据相机高度与相机成像原理计算车道线的3D坐标。PolyFitCameraLaneline(frame)主要功能是3D车道线的拟合,但是由于车道平面视为水平面,其车道线上Y坐标为常数,所以车道线方程是关于X和Z的方程,拟合思路其实和2D车道线拟合思路一致,因为外点已经剔除,没有必要再用随机采用一致性算法,同时也是采用矩阵求逆的方法求解直线方程的系数,Apollo中采用了QR分解。直线拟合代码如下:
template <typename Dtype>
bool PolyFit(const std::vector<Eigen::Matrix<Dtype, 2, 1>>& pos_vec, const int& order,
Eigen::Matrix<Dtype, max_poly_order + 1, 1>* coeff, const bool& is_x_axis = true){
if (coeff == nullptr) {
AERROR << "The coefficient pointer is NULL.";
return false;
}
if (order > max_poly_order) {
AERROR << "The order of polynomial must be smaller than " << max_poly_order;
return false;
}
int n = static_cast<int>(pos_vec.size());
// 保证方程有解
if (n <= order) {
AERROR << "The number of points should be larger than the order. #points = "
<< pos_vec.size();
return false;
}
// 构建 Ax = b 的线性方程组
Eigen::Matrix<Dtype, Eigen::Dynamic, Eigen::Dynamic> A(n, order + 1);
Eigen::Matrix<Dtype, Eigen::Dynamic, 1> y(n);
Eigen::Matrix<Dtype, Eigen::Dynamic, 1> result;
for (int i = 0; i < n; ++i) {
for (int j = 0; j <= order; ++j) {
A(i, j) = static_cast<Dtype>(
std::pow(is_x_axis ? pos_vec[i].x() : pos_vec[i].y(), j));
}
y(i) = is_x_axis ? pos_vec[i].y() : pos_vec[i].x();
}
// solve linear least squares
// QR分解求解系数
result = A.householderQr().solve(y);
assert(result.size() == order + 1);
for (int j = 0; j <= max_poly_order; ++j) {
(*coeff)(j) = (j <= order) ? result(j) : static_cast<Dtype>(0);
}
return true;
}至此,车道线检测的细节部分已经分析完毕。
总结
处于安全考虑,Apollo中车道的判定相当谨慎。
车道线从2D到3D的拟合非常细节,是从效率、鲁棒性和准确性的综合考虑。
pitch计算依赖于:1.车辆走直线;2.车道线的检测成功。能适应与规范化城市道路。
① 全网独家视频课程
BEV感知、毫米波雷达视觉融合、多传感器标定、多传感器融合、多模态3D目标检测、点云3D目标检测、目标跟踪、Occupancy、cuda与TensorRT模型部署、协同感知、语义分割、自动驾驶仿真、传感器部署、决策规划、轨迹预测等多个方向学习视频(扫码即可学习)
 视频官网:www.zdjszx.com
视频官网:www.zdjszx.com
② 国内首个自动驾驶学习社区
近2000人的交流社区,涉及30+自动驾驶技术栈学习路线,想要了解更多自动驾驶感知(2D检测、分割、2D/3D车道线、BEV感知、3D目标检测、Occupancy、多传感器融合、多传感器标定、目标跟踪、光流估计)、自动驾驶定位建图(SLAM、高精地图、局部在线地图)、自动驾驶规划控制/轨迹预测等领域技术方案、AI模型部署落地实战、行业动态、岗位发布,欢迎扫描下方二维码,加入自动驾驶之心知识星球,这是一个真正有干货的地方,与领域大佬交流入门、学习、工作、跳槽上的各类难题,日常分享论文+代码+视频,期待交流!

③【自动驾驶之心】技术交流群
自动驾驶之心是首个自动驾驶开发者社区,聚焦目标检测、语义分割、全景分割、实例分割、关键点检测、车道线、目标跟踪、3D目标检测、BEV感知、多模态感知、Occupancy、多传感器融合、transformer、大模型、点云处理、端到端自动驾驶、SLAM、光流估计、深度估计、轨迹预测、高精地图、NeRF、规划控制、模型部署落地、自动驾驶仿真测试、产品经理、硬件配置、AI求职交流等方向。扫码添加汽车人助理微信邀请入群,备注:学校/公司+方向+昵称(快速入群方式)

④【自动驾驶之心】平台矩阵,欢迎联系我们!





















 2934
2934

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








