数据结构&算法学习笔记: 图

原创 于 2019-08-30 11:40:44 发布 · 202 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#数据结构 #图

本文深入解析图数据结构，包括无向图、有向图、带权图的概念，以及邻接矩阵和邻接表两种存储方式。通过代码示例，详细介绍了如何实现图的插入结点、添加边、获取邻接点等操作，同时演示了广度优先搜索(BFS)和深度优先搜索(DFS)算法的应用。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

注：该篇文章已与我的个人博客同步更新。欢迎移步https://cqh-i.github.io/体验更好的阅读效果。

图

图是一种数据结构,其中结点可以具有零个或多个相邻元素.两个结点之间的链接称为边.

图的常用概念

1)顶点

2)边

3)路径: 比如从D->C的路径有 ①D->B->C ② D->A->B->C

4)无向图: 顶点之间的连接没有方向,比如A-B,既可以是A->B, 也可以是B->A.

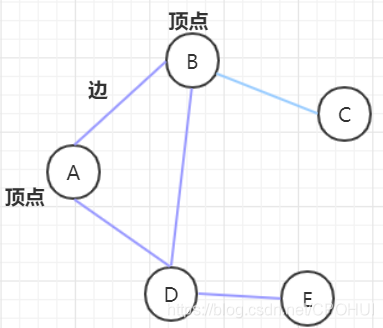
5)有向图:顶点间的连接有方向, 比如A-B, 只能是A->B.

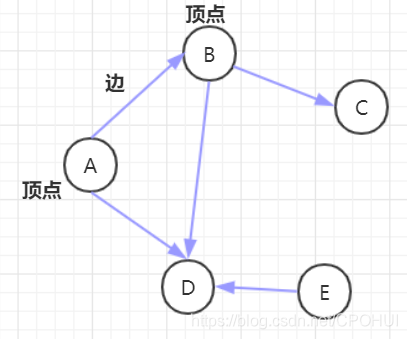
6)带权图: 边带权值

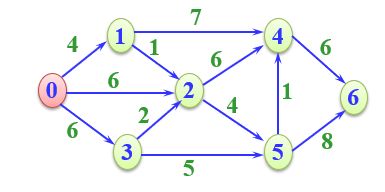
图的存储结构

邻接矩阵

邻接矩阵是表示图形中顶点之间相邻关系的矩阵.

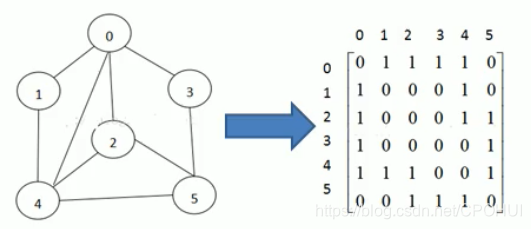
邻接矩阵无向图的代码分析

存储结构
public class Graph {
    private ArrayList<String> vertexList; // 存储顶点集合
    private int[][] edges; // 存储图对应的邻结矩阵
    private int numOfEdges; // 表示边的数目
}
构造器
/**
* 构造器完成初始化工作
* @param n 顶点的个数
*/
public Graph(int n) {
    // 初始化矩阵和vertexList
    edges = new int[n][n];
    vertexList = new ArrayList<String>(n);
    numOfEdges = 0;
}
插入结点与添加边方法
// 插入结点
public void insertVertex(String vertex) {
    vertexList.add(vertex);
}

// 添加边
/**
 * @param v1 第一个顶点对应的下标
 * @param v2 第二个顶点对应的下标
 * @param weight 表示权值或者有边关系的值
 */
public void insertEdge(int v1, int v2, int weight) {
    edges[v1][v2] = weight;
    edges[v2][v1] = weight;
    numOfEdges++;
}
返回一个点所有邻接点的下标
/**   
 * @Description: 返回一个点的所有邻接点的下标  
 */
public ArrayList<Integer> getAllNextNode(int index) {
    ArrayList<Integer> arrayList = new ArrayList<Integer>();
    for (int i = 0; i < vertexList.size(); i++) {
        if (edges[index][i] != 0) {
            arrayList.add(i);
        }
    }
    return arrayList;
}
BFS

用队列先进先出特性, 将结点添加进队列, 输出并删除第一个结点后, 然后将它所有没进过队列的邻接点都添加进队列中, 来保证广度优先搜索的过程.

/**   
 * @Description: 广度优先搜索
 * @param graph 图
 * @param index  起点下标
 */
public void bfs(Graph graph, Integer index) {
    Queue<Integer> queue = new LinkedList<Integer>();
    queue.offer(index);
    Set<Integer> set = new HashSet<Integer>();
    set.add(index);
    while (queue.size() > 0) {
        int outIndex = queue.poll();
        System.out.println(graph.getValueByIndex(outIndex));// 返回第一个元素，并在队列中删除
        ArrayList<Integer> arrayList = graph.getAllNextNode(outIndex);
        for (Integer integer : arrayList) {
            if (!set.contains(integer)) {
                queue.offer(integer);
                set.add(integer);
            }
        }
    }
}
DFS

用栈后进先出特性, 将结点添加进队列, 输出并删除第一个结点后, 然后将它所有没进过栈的邻接点都添加进队列中, 来保证深度优先搜索的过程.

/**   
 * @Description: 深度优先搜索
 * @param graph 图
 * @param index  起点下标
 */
public void dfs(Graph graph, Integer index) {
    Stack<Integer> stack = new Stack<Integer>();
    stack.push(index);
    Set<Integer> set = new HashSet<Integer>();
    set.add(index);
    while (stack.size() > 0) {
        int outIndex = stack.pop();
        System.out.println(graph.getValueByIndex(outIndex));// 返回第一个元素，并在栈中删除
        ArrayList<Integer> arrayList = graph.getAllNextNode(outIndex);
        for (Integer integer : arrayList) {
            if (!set.contains(integer)) {
                stack.push(integer);
                set.add(integer);
            }
        }
    }
}
图的其它常用的方法
// 返回结点的个数
public int getNumOfVertex() {
    return vertexList.size();
}

// 显示图对应的矩阵
public void showGraph() {
    for (int[] link : edges) {
        System.err.println(Arrays.toString(link));
    }
}

// 得到边的数目
public int getNumOfEdges() {
    return numOfEdges;
}

// 返回结点i(下标)对应的数据 0->"A" 1->"B" 2->"C"
public String getValueByIndex(int i) {
    return vertexList.get(i);
}

// 返回v1和v2的权值
public int getWeight(int v1, int v2) {
    return edges[v1][v2];
}
完整代码和测试
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashSet;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Set;
import java.util.Stack;

public class Graph {

    public static void main(String[] args) {
        // 测试一把图是否创建ok
        int n = 5; // 结点的个数
        String Vertexs[] = { "A", "B", "C", "D", "E" };

        // 创建图对象
        Graph graph = new Graph(n);
        // 循环的添加顶点
        for (String vertex : Vertexs) {
            graph.insertVertex(vertex);
        }

        // 添加边
        // A-B A-C B-C B-D B-E
        graph.insertEdge(0, 1, 1); // A-B
        graph.insertEdge(0, 2, 1); // A-C
        graph.insertEdge(1, 2, 1); // B-C
        graph.insertEdge(1, 3, 1); // B-D
        graph.insertEdge(1, 4, 1); // B-E
        // 显示一把邻结矩阵
        graph.showGraph();
        graph.bfs(graph, 0);
        System.out.println("-------");
        graph.dfs(graph, 0);
    }

    private ArrayList<String> vertexList; // 存储顶点集合
    private int[][] edges; // 存储图对应的邻结矩阵
    private int numOfEdges; // 表示边的数目

    /**
     * 构造器完成初始化工作
     * @param n 顶点的个数
     */
    public Graph(int n) {
        // 初始化矩阵和vertexList
        edges = new int[n][n];
        vertexList = new ArrayList<String>(n);
        numOfEdges = 0;
    }

    // 插入结点
    public void insertVertex(String vertex) {
        vertexList.add(vertex);
    }

    // 添加边
    /**
     * @param v1 第一个顶点对应的下标
     * @param v2 第二个顶点对应的下标
     * @param weight 表示权值或者有边关系的值
     */
    public void insertEdge(int v1, int v2, int weight) {
        edges[v1][v2] = weight;
        edges[v2][v1] = weight;
        numOfEdges++;
    }

    // 图中常用的方法
    // 返回结点的个数
    public int getNumOfVertex() {
        return vertexList.size();
    }

    // 显示图对应的矩阵
    public void showGraph() {
        for (int[] link : edges) {
            System.out.println(Arrays.toString(link));
        }
    }

    // 得到边的数目
    public int getNumOfEdges() {
        return numOfEdges;
    }

    // 返回结点i(下标)对应的数据 0->"A" 1->"B" 2->"C"
    public String getValueByIndex(int i) {
        return vertexList.get(i);
    }

    // 返回v1和v2的权值
    public int getWeight(int v1, int v2) {
        return edges[v1][v2];
    }

    /**   
     * @Description: 返回一个点的所有邻接点的下标  
     */
    public ArrayList<Integer> getAllNextNode(int index) {
        ArrayList<Integer> arrayList = new ArrayList<Integer>();
        for (int i = 0; i < vertexList.size(); i++) {
            if (edges[index][i] != 0) {
                arrayList.add(i);
            }
        }
        return arrayList;
    }

    /**   
     * @Description: 广度优先搜索
     * @param graph 图
     * @param index  起点下标
     */
    public void bfs(Graph graph, Integer index) {
        Queue<Integer> queue = new LinkedList<Integer>();
        queue.offer(index);
        Set<Integer> set = new HashSet<Integer>();
        set.add(index);
        while (queue.size() > 0) {
            int outIndex = queue.poll();
            System.out.println(graph.getValueByIndex(outIndex));// 返回第一个元素，并在队列中删除
            ArrayList<Integer> arrayList = graph.getAllNextNode(outIndex);
            for (Integer integer : arrayList) {
                if (!set.contains(integer)) {
                    queue.offer(integer);
                    set.add(integer);
                }
            }
        }
    }

    /**   
     * @Description: 深度优先搜索
     * @param graph 图
     * @param index  起点下标
     */
    public void dfs(Graph graph, Integer index) {
        Stack<Integer> stack = new Stack<Integer>();
        stack.push(index);
        Set<Integer> set = new HashSet<Integer>();
        set.add(index);
        while (stack.size() > 0) {
            int outIndex = stack.pop();
            System.out.println(graph.getValueByIndex(outIndex));// 返回第一个元素，并在栈中删除
            ArrayList<Integer> arrayList = graph.getAllNextNode(outIndex);
            for (Integer integer : arrayList) {
                if (!set.contains(integer)) {
                    stack.push(integer);
                    set.add(integer);
                }
            }
        }
    }

}

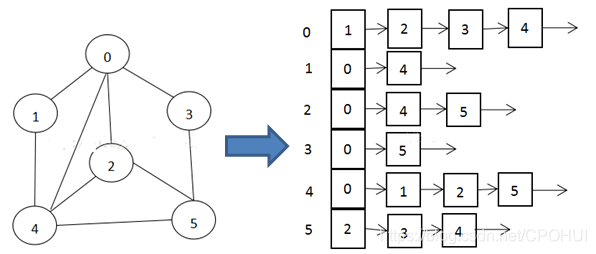
邻接表

1)邻接矩阵需要为每个顶点都分配n个边的空间, 其实有很多边都是不存在,会造成空间的一定损失.

2)邻接表的实只心存在的边, 不关心不存在的边接表由数组链表组

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值