【代码超详解】CometOJ C0275 [USACO]特殊的质数肋骨（质数的判定 + 枚举 + 剪枝）

最新推荐文章于 2024-12-21 15:42:55 发布

原创最新推荐文章于 2024-12-21 15:42:55 发布 · 395 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#详解

ACM-ICPC 专栏收录该内容

238 篇文章

订阅专栏

博客详细讲解了如何解决USACO竞赛中的特殊质数问题，针对N的范围从1到8，特别是当N=8时，通过两种方法避免暴力枚举导致的时间超限。第一种方法是高位枚举质数并快速验证，一旦发现不符合条件立即终止。第二种方法是自底向上枚举，并在枚举过程中及时剪枝。两种方法都强调了高效的质数判定和剪枝策略。

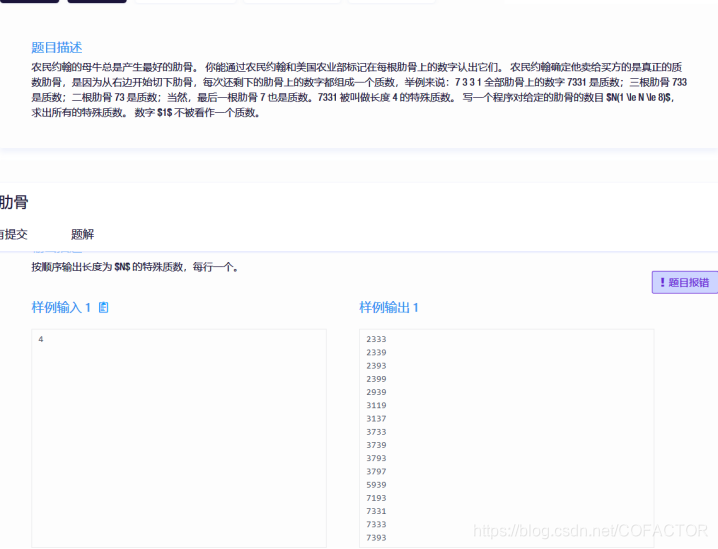
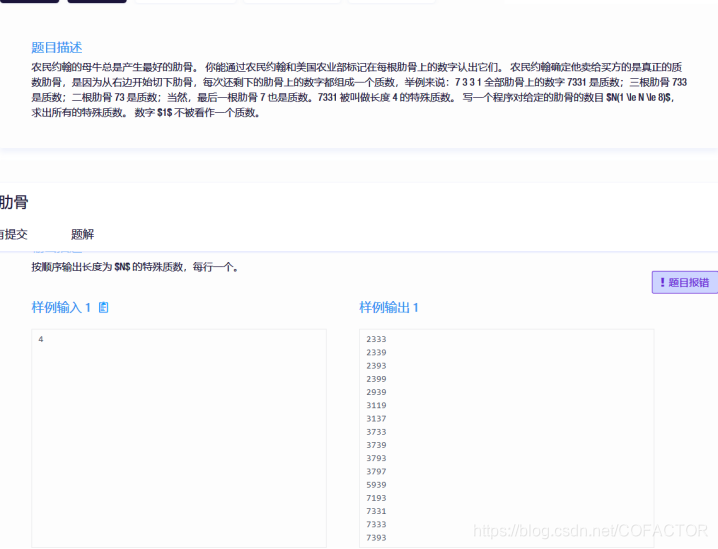
一、题目描述

1000 ms，256 MB
在这里插入图片描述

二、算法分析说明与代码编写指导

N 的范围是 1 到 8，当 N = 8 时，需要验证并列举 10000000 到 99999999 的全部“特殊质数”，直接暴力枚举会超时。
一种方法是：当 N 比较大的时候，只对高位（这里选高 5 位）枚举质数，然后进行验证。当然验证过程不能直接模拟题目所说的“从右边开始切下肋骨”的过程，因为判定较大数的素性是比较费时间的。如果对一个数，截去末尾若干位后判定仍然是质数，但差不多截完了以后又发现剩余的位不是质数，显然是不经济的。所以，应该先截取高位开始更快速地判断，一旦发现不是“特殊质数”，立刻终止判断并返回 false。
另一种方法来自：https://blog.youkuaiyun.com/shuati2000/article/details/97816699
从 1 位数开始枚举到 N 位数，枚举过程中发现正在枚举的数已经不是“特殊质数”则跳过该数。这种剪枝方法可以省去非常大的枚举量。最高位自然只有 2，3，5，7。以 N = 8，且正在枚举第二位为例。如果枚举到 21，验证 21 不是质数，那么剩余 6 位都不用再进行枚举，而直接开始枚举高位为 23 的数。

三、AC 代码

法一

#include<cstdio>
#include<algorithm>
#pragma warning(disable:4996)
using namespace std;
unsigned prime[9592] = { 2,3 }, _PTy, MaxPrime, * prime_end = prime + sizeof(prime) / sizeof(prime[0]);
inline void genprime() {
	decltype(_PTy) a = 4, t; bool flag = true;
	for (auto i = prime + 2; i != prime_end;) {
		t = sqrt(a); flag = true;
		for (auto j = prime; *j <= t; ++j)if (a % *j == 0) { flag = false; break; }
		if (flag) { *i = a, ++i; }
		++a;
	}
	MaxPrime = *(prime_end - 1);
}
inline bool isprime(const decltype(_PTy)& x) {
	if (x <= MaxPrime)return binary_search(prime, prime_end, x);
	else {
		static decltype(_PTy) t; t = min((decltype(_PTy))sqrt(x), MaxPrime);
		for (size_t j = 0; prime[j] <= t; ++j)if (x % prime[j] == 0)return false;
		return true;
	}
}
const unsigned e[9] = { 1,10,100,1e3,1e4,1e5,1e6,1e7,1e8 }; unsigned n;
inline bool isSpecialPrime(const unsigned& x) {
	static unsigned s = n - 1;
	for (unsigned i = s; i != 0; --i) {
		if (!isprime(x / e[i]))return false;
	}
	return isprime(x);
}
int main() {
	genprime();
	scanf("%u", &n);
	if (n <= 5) {
		for (auto i = e[n - 1] + 1; i < e[n]; i += 2) {
			if (isSpecialPrime(i))printf("%u\n", i);
		}
	}
	else {
		for (auto I = lower_bound(prime, prime_end, 10000); I != prime_end; ++I) {
			static const unsigned p = e[n - 5]; static unsigned t; t = (*I + 1) * p;
			for (auto i = *I * p + 1; i < t; i += 2) {
				if (isSpecialPrime(i))printf("%u\n", i);
			}
		}
	}
	return 0;
}

法二

#include<cstdio>
#include<algorithm>
#include<typeinfo>
#pragma warning(disable:4996)
using namespace std;
unsigned prime[1230] = { 2,3 }, _PTy, MaxPrime, * prime_end = prime + sizeof(prime) / sizeof(prime[0]);
inline void genprime() {
	decltype(_PTy) a = 4, t; bool flag = true;
	for (auto i = prime + 2; i != prime_end;) {
		t = sqrt(a); flag = true;
		for (auto j = prime; *j <= t; ++j)if (a % *j == 0) { flag = false; break; }
		if (flag) { *i = a, ++i; }
		++a;
	}
	MaxPrime = *(prime_end - 1);
}
inline bool isprime(const decltype(_PTy)& x) {
	if (x <= MaxPrime)return binary_search(prime, prime_end, x);
	else {
		static decltype(_PTy) t; t = min((decltype(_PTy))sqrt(x), MaxPrime);
		for (auto j = prime; *j <= t; ++j)if (x % *j == 0)return false;
		return true;
	}
}
unsigned n;
void Enum(const unsigned& x, const unsigned& d) {
	if (d == n && isprime(x)) { printf("%u\n", x); return; }
	unsigned s = x * 10 + 1, t = s + 8;
	for (unsigned i = s; i <= t; i += 2) {
		if (isprime(i))Enum(i, d + 1);
	}
}
int main() {
	genprime(); scanf("%u", &n);
	Enum(2, 1); Enum(3, 1); Enum(5, 1); Enum(7, 1);
	return 0;
}