堆的详解，题目，堆排序

堆的概念

1，首先，堆是一颗完全二叉树
2，堆中：所有的父亲大于等于或者小于等于孩子

当我们实现堆的时候，操作的是数组，想的应该是堆（完全二叉树）

堆的详解（以小堆为例）

头文件

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>

//模拟小堆的实现哦

typedef int HPDataType;

typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;

//初始化
void InitHeap(HP* php);

//销毁
void DestroyHeap(HP* php);

//打印
void PrintHeap(HP* php);

//插入
void PushHeap(HP* php, HPDataType x);

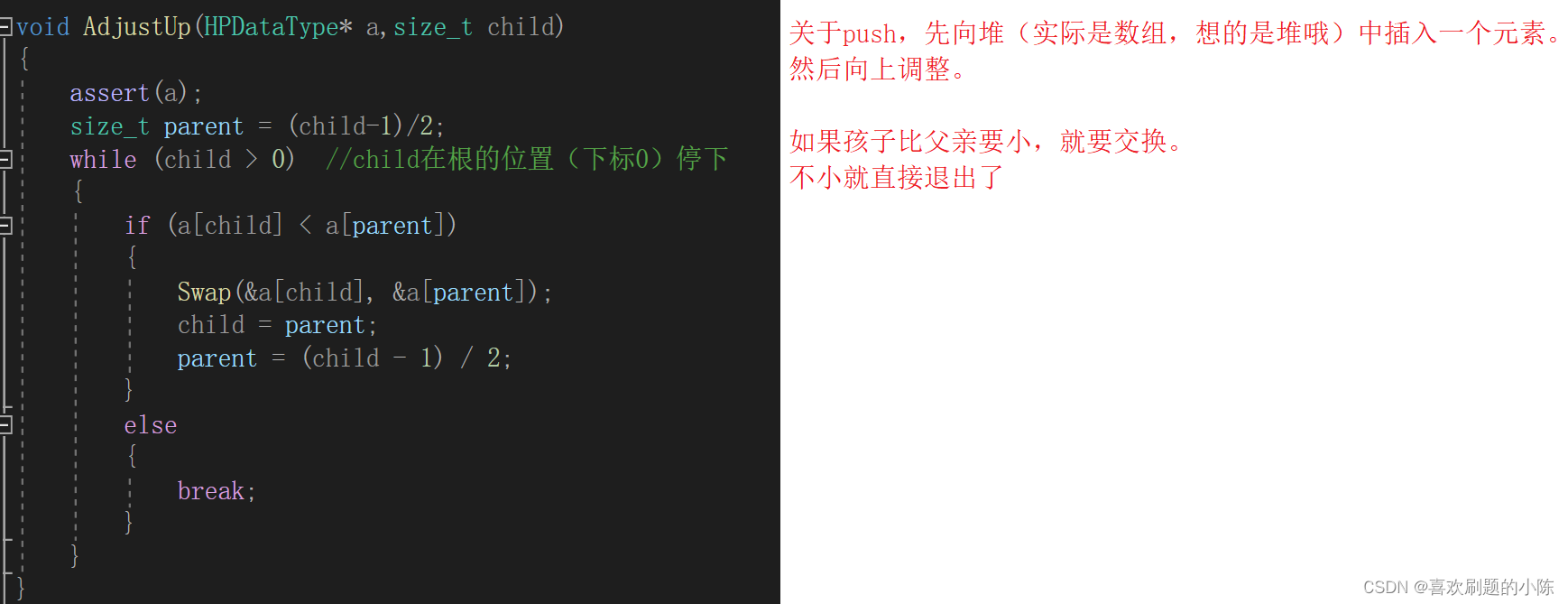
//向上调整
void AdjustUp(HPDataType* a, size_t child);

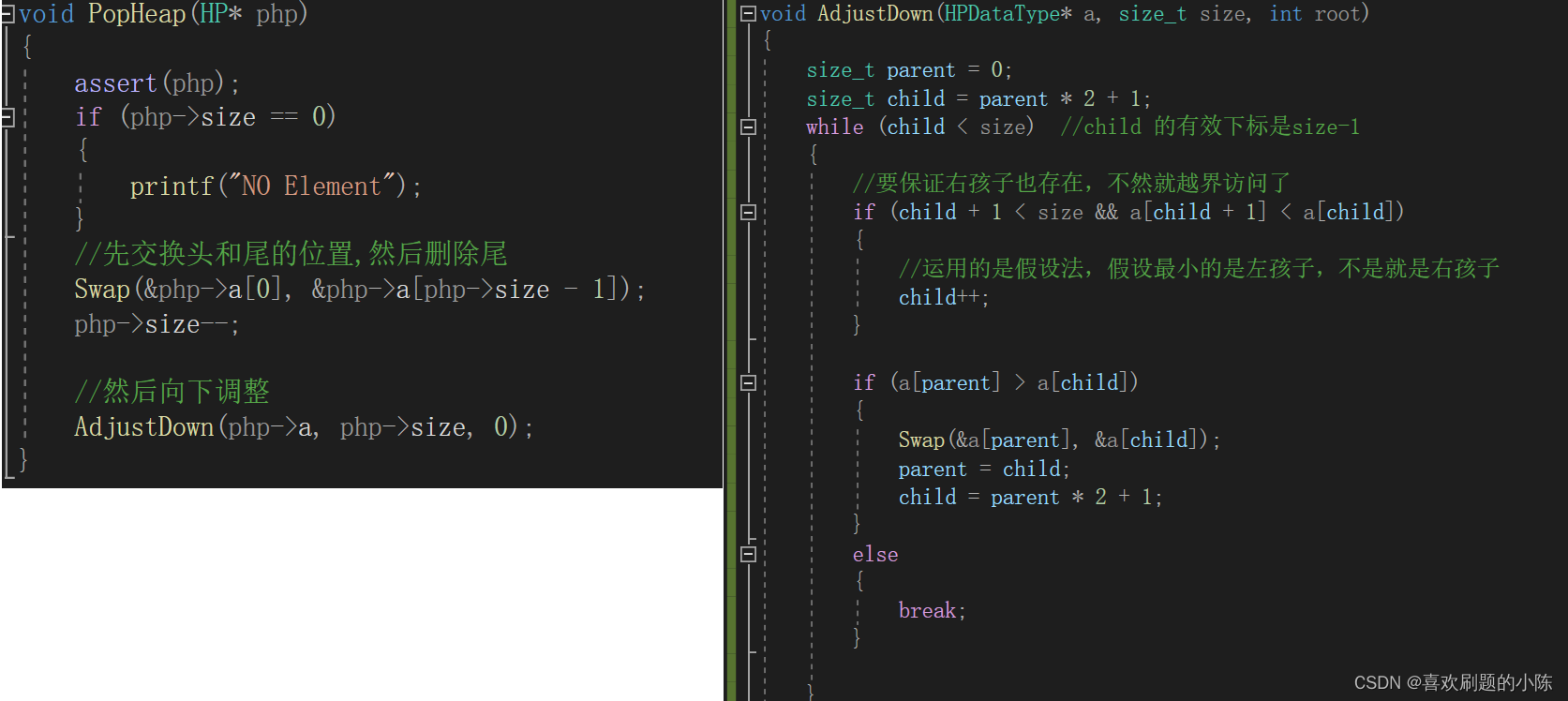
//向下调整
void AdjustDown(HPDataType* a, size_t size, int root);
//交换两个数

void Swap(HPDataType* pa, HPDataType* pb);

//删除堆顶
void PopHeap(HP* php);

//取堆顶元素
HPDataType HeapTop(HP* php);

// 堆的数据个数
int HeapSize(HP* php);

// 堆的判空
bool HeapEmpty(HP* php);

这里难的操作就是push(插入)和pop（删除）哦。

push是尾部直接插入，然后向上调整
pop先让根和尾交换位置，然后删除尾。
然后从根向下调整。

左右孩子和父亲的关系（一定要详细理解哦）。

leftchild=parent2+1
rightchild=parent2+2
parent=(child-1)/2

push是尾部直接插入，然后向上调整

关于pop
1，先交换头和尾
2，删除尾，
33向下调整

函数定义的全部代码

void InitHeap(HP* php)
{
	assert(php);
	php->a = NULL;
	php->size = 0;
	php->capacity = 0;
}

void DestroyHeap(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}

void PrintHeap(HP* php)
{
	assert(php);
	for (int i = 0; i < php->size; i++)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
}

void Swap(HPDataType* pa, HPDataType* pb)
{
	HPDataType tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}

void AdjustUp(HPDataType* a,size_t child)
{
	assert(a);
	size_t parent = (child-1)/2;
	while (child > 0)  //child在根的位置（下标0）停下
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void PushHeap(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a,sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}

	php->a[php->size] = x;
	php->size++;

	//开始向上调整
	 AdjustUp(php->a,php->size-1);
}

void AdjustDown(HPDataType* a, size_t size, int root)
{
	size_t parent = 0;
	size_t child = parent * 2 + 1;
	while (child < size)  //child 的有效下标是size-1
	{
		//要保证右孩子也存在，不然就越界访问了
		if (child + 1 < size && a[child + 1] < a[child])
		{
			//运用的是假设法，假设最小的是左孩子，不是就是右孩子
			child++;
		}

		if (a[parent] > a[child])
		{
			Swap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}

	}
}
void PopHeap(HP* php)
{
	assert(php);
	if (php->size == 0)
	{
		printf("NO Element");
	}
	//先交换头和尾的位置,然后删除尾
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;

	//然后向下调整
	AdjustDown(php->a, php->size, 0);
}

//取堆顶元素
HPDataType HeapTop(HP* php)
{
	return php->a[0];
}

// 堆的数据个数
int HeapSize(HP* php)
{
	return php->size;
}

// 堆的判空
bool HeapEmpty(HP* php)
{
	return 0== php->size;
}

关于堆的题目

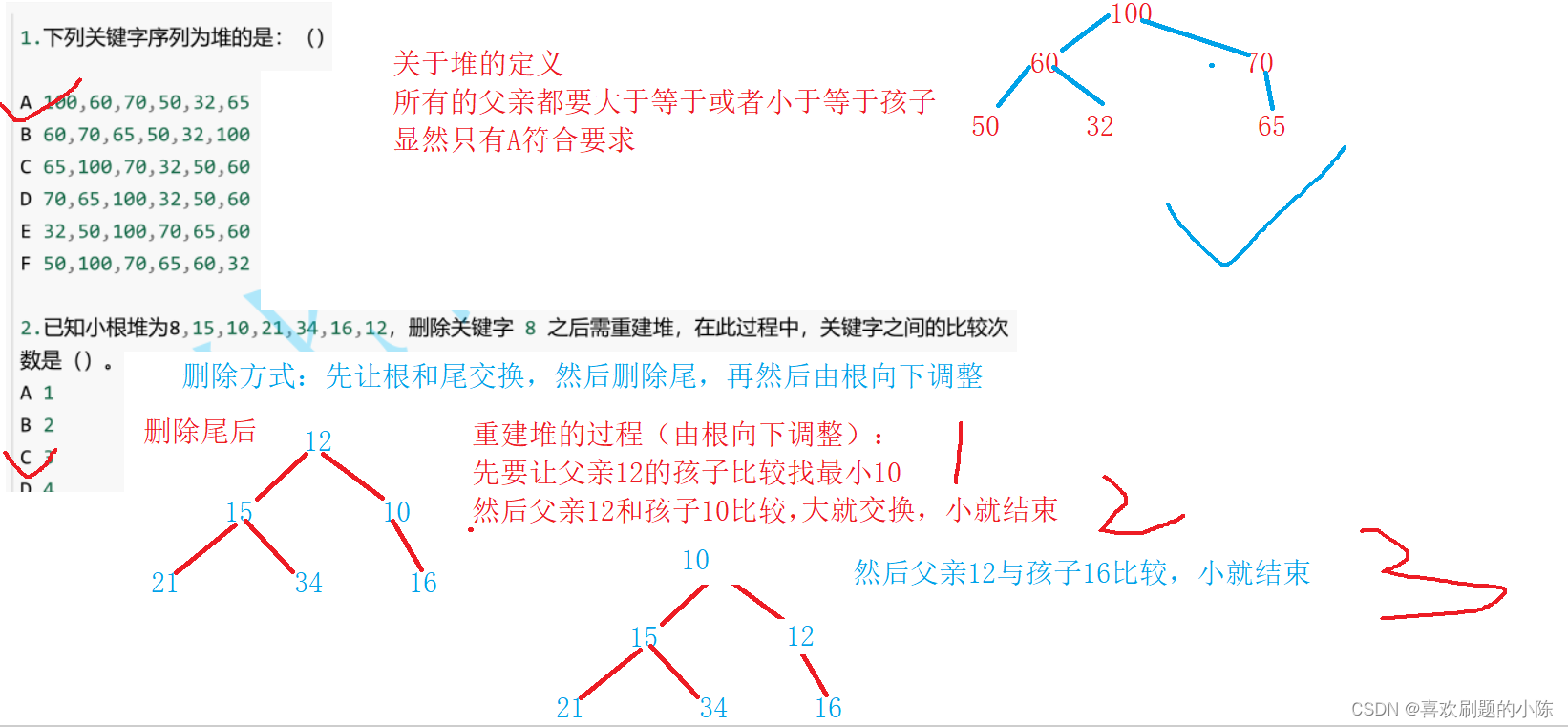
利用堆的性质来排序

升序：小堆
降序：大堆

核心思路：先将数组中所有的元素push到堆中，然后依次取堆顶元素就ok啦

时间复杂度是N*logN

void HeapSort(int* a, int sz)
{  
	assert(a);
	HP H;
	InitHeap(&H);
	for (int i = 0; i < sz; i++)
	{
		PushHeap(&H, a[i]);
	}
	for (int k = 0; k < sz; k++)
	{
		int top = HeapTop(&H);
		a[k] = top;
		PopHeap(&H);
	}
	DestroyHeap(&H);
}

void test2()
{
	//
	int arr[] = { 15,20,31,21,2,1,4,45,21,31,12,14 };
	int sz = sizeof(arr) / sizeof(arr[0]);
	HeapSort(arr, sz);
	for (int i = 0; i < sz; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
}

int main()
{
	//test1();
	test2();
	return 0;
}