剑指 Offer 57 - II. 和为s的连续正数序列

最新推荐文章于 2021-12-17 11:14:10 发布

原创最新推荐文章于 2021-12-17 11:14:10 发布 · 160 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#滑动窗口 #连续子序和

剑指offer 专栏收录该内容

7 篇文章

订阅专栏

本文介绍了一种寻找连续正整数序列使序列之和等于特定目标值的方法。提出了两种解决方案：一种是通过设定子序列长度，计算并验证序列之和；另一种是使用滑动窗口或公式法来高效解决问题。

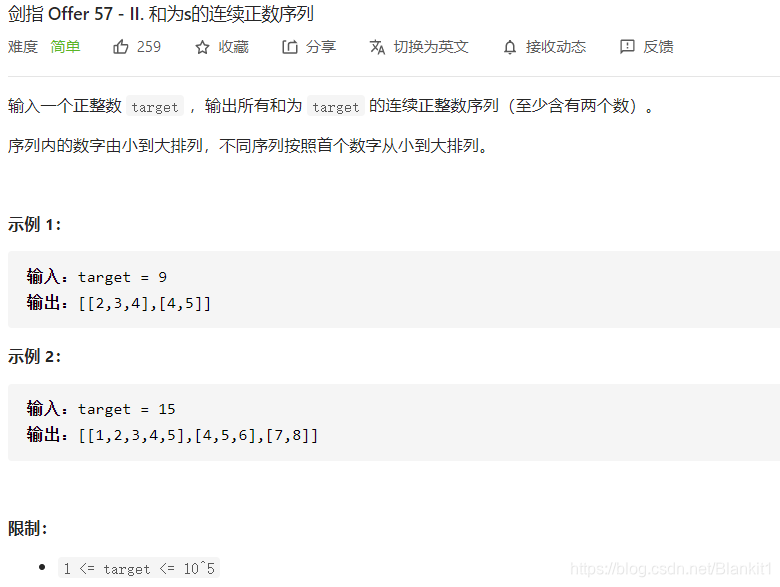
题目

在这里插入图片描述

我的解法

题目要求返回的是连续的子列和。根据子列的长度k，可以确定子列的中间值mid。判断mid前k/2到后k/2个数的和是否为target，决定该子列是否加入到result中.

子序列的长度k最大为target//2
子序列的长度k为奇数，子序列的起始分别为mid - k//2 ,mid + k//2+1
子序列的长度k为偶数，子序列的起始分别为mid - k//2 + 1,mid + k//2+1

class Solution:
    def findContinuousSequence(self, target: int):
        import math
        if target <= 2:
            return []
        result = []
        for k in range(2,math.ceil(target//2)):
            mid = target//k
            if k%2:
                if mid - k // 2 <= 0:
                    continue
                # if sum(range(mid - k//2 if mid - k//2 >0 else 1 ,mid + k//2+1)) == target:
                if sum(range(mid - k//2 ,mid + k//2+1)) == target:
                    result.append(list(range(mid - k//2,mid + k//2+1)))
            else:
                if mid - k // 2 +1 <= 0:
                    continue
                if sum(range(mid - k//2 + 1,mid + k//2+1)) == target:
                    result.append(list(range(mid - k//2 + 1,mid + k//2+1)))
        return sorted(result)

大神解法1 – 滑动窗口

滑动窗口的起始端都只能向右移动。滑动窗口的和 > target，左侧向右移，窗口减去一个数。小于则是右侧向右移动，添加一个数到窗口中

大神解法2 – 公式法

序列是连续的，在知道左边界与和target的情况下，通过公式求得右边界。
右边界需满足：

大于0
是整数
不能是单根

class Solution:
    def findContinuousSequence(self, target: int):
        i, j, res = 1, 2, []
        while i < j:
            j = (-1 + (1 + 4 * (2 * target + i * i - i)) ** 0.5) / 2
            if i < j and j == int(j):
                res.append(list(range(i, int(j) + 1)))
            i += 1
        return res

作者：jyd
链接：https://leetcode-cn.com/problems/he-wei-sde-lian-xu-zheng-shu-xu-lie-lcof/solution/jian-zhi-offer-57-ii-he-wei-s-de-lian-xu-t85z/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。