笔记(总结)-注意力机制(Attention)简述

本篇主要针对注意力（Attention）机制进行简要描述。Attention是为了解决Sequence-to-Sequence中的一些问题而提出的，本身的逻辑十分简洁。Attention的产生过程反映了解决问题的一种最直接的思路，正如Resnet中提出“残差”的概念一样，简单直接的就能解决问题，而且思路没有绕任何弯子。这在科研工作中是十分难得的。下面结合机器翻译问题来回顾下这整个过程。

---

Seq2seq

先回顾下Sequence-to-Sequence，这是RNN-Based模型架构中错开的many to many的一种应用，主要是为了将一个序列转换为另一个序列，即下图中第四种：

这种架构也叫Encoder-Decoder模型。具体来说，Encoder部分为红色block及对应的绿色block，Decoder部分为蓝色block及对应的绿色block。Seq2sep主要想解决的是输入输出序列不等长的问题，它通过Encoder将输入序列编码成一个固定的向量$c$，然后将$c$作为Decoder的初始隐状态输入，解码为输出序列。即：

但这样的架构是有问题的。主要有两点：

1. Encoder将所有输入序列编码成一个统一的语义特征$c$，再将其运用到Decoder中。这就要求$c$必须能很好地概括输入序列，然而RNN模型是有长度依赖的，当序列过长时难以概括所有信息。
2. 不同的Decoder输出使用的是同样的$c$，但实际中并非如此。以机器翻译为例，翻译目标词的第一个词往往和源语言中第一个词有较大的关联，而不太关心其它位置的词。Decoder中不同的输出需要的是不同的输入特征，且不一定需要编码了整个输入序列的$c$。

因此，最理想的情况是，在解码输出不同的词时，能够从输入序列中自动选择相关联的词，并且提高这部分词在建模时的特征权重。这样就得出了Attention Model的动机。

---

Attention Mechanism

由上文Seq2seq的缺陷可以知道，要解决第一个问题，即Decoder使用的是统一的$c$，需要在不同的时刻输入不同的$c_i$；要解决第二个问题，即Decoder不同时刻的输出关注输入序列的不同部分，需要$c_i$能自动选取最相关的输入序列。

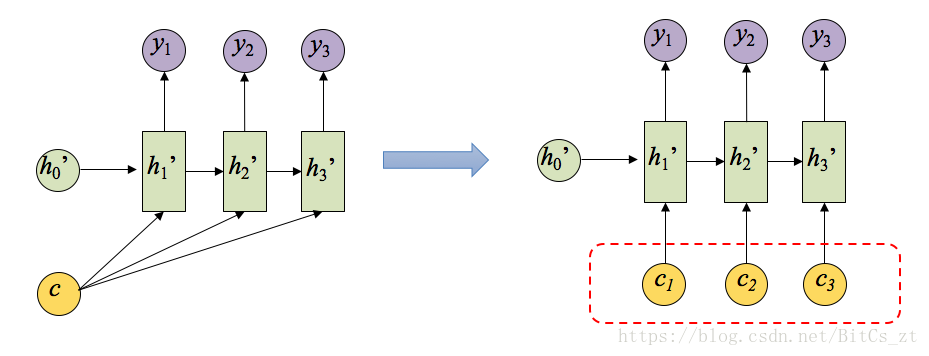
现在核心问题转变为，应该如何求解$c_i$。首先应该明确，$c_i$和$c$一样，是来源于Encoder的隐状态$h_j$，不同时刻的$h_j$编码了对应的输入序列。最直观的想法是给每个$h_j$赋予权重，加权得到$c_i$，权重越大说明对$c_i$的贡献越大。即：

$$c_i=\sum_{j=1}^La_{ij}h_j$$

一个简单的示意图如下：

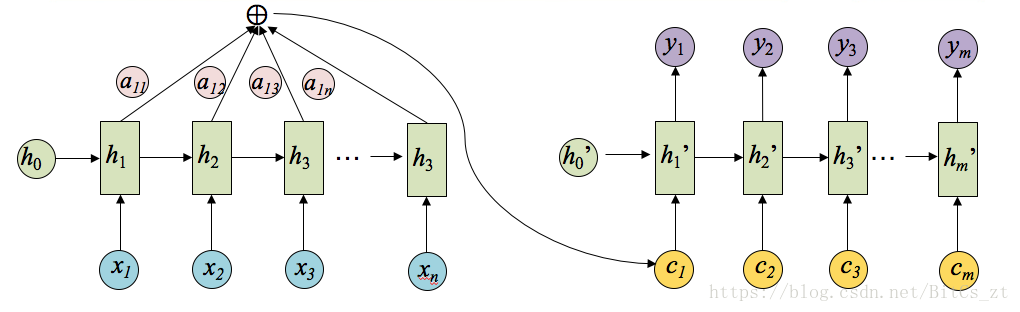
此时问题转化如何求权重$a_{ij}$。$a_{ij}$其实可以看做一个概率，反映了$h_j$对$c_i$的重要性。看到概率很自然联想到使用softmax，即：

$$a_{ij}=\frac{\exp(e_{ij})}{\sum_{k=1}^L\exp(e_{ik})}$$

其中：

$$e_{ij}=f(h_{i-1}^{'},h_j)$$

$f$表示是一个匹配度的打分函数，可以是一个很复杂的NN，也可以是一个简单的计算，这里不深入讨论。由于利用$c_i$进行计算时，还没有$h_i^{'}$，因此使用最接近的$h_{i-1}^{'}$。

上述思考过程是执果索因，将各个步骤的结果逐步回代即可得到模型。可以看到Attention机制的加入并没有影响大的模型架构，相当于一个小配件，与原有架构的耦合度是很低的。这也使得我们在设计具体的函数时更好施展。

---

这就是最原始的Attention，我们希望借助这种机制，让模型能够学习到：在不同的任务进行状态中，要把注意力放在不同的可利用信息上。这便是Attention的逻辑精华。原始Attention还有很多可以改进的地方，在这之后也有很多杰出的科研成功。但由于本篇主要侧重点是Attention的建模动机与思路，就不详细展开了。

参考如下，在此表示感谢：

• 中国科学院大学-自然语言处理（胡玥老师）的课程讲义
• 中国科学院大学-深度学习与自然语言处理（曹亚男老师）的课程讲义