在本篇内容中,我们将介绍第一个机器学习算法——线性回归算法。更重要的是,我们将借助这个算法,带你了解一个完整的监督学习流程。
一、模型表示
我们通过一个例子来开始:预测房价。我们拥有一个数据集,记录了美国俄勒冈州波特兰市的若干房子面积及其对应的成交价格。横轴表示房子的面积(平方英尺),纵轴表示房价(千美元)。如果有一套房子面积是 1250 平方英尺,想知道大概能卖多少钱。你可以通过构建一个预测模型来实现,比如你可以用一条直线来拟合数据,从而推断出:这套房子可能值大约 22 万美元左右。
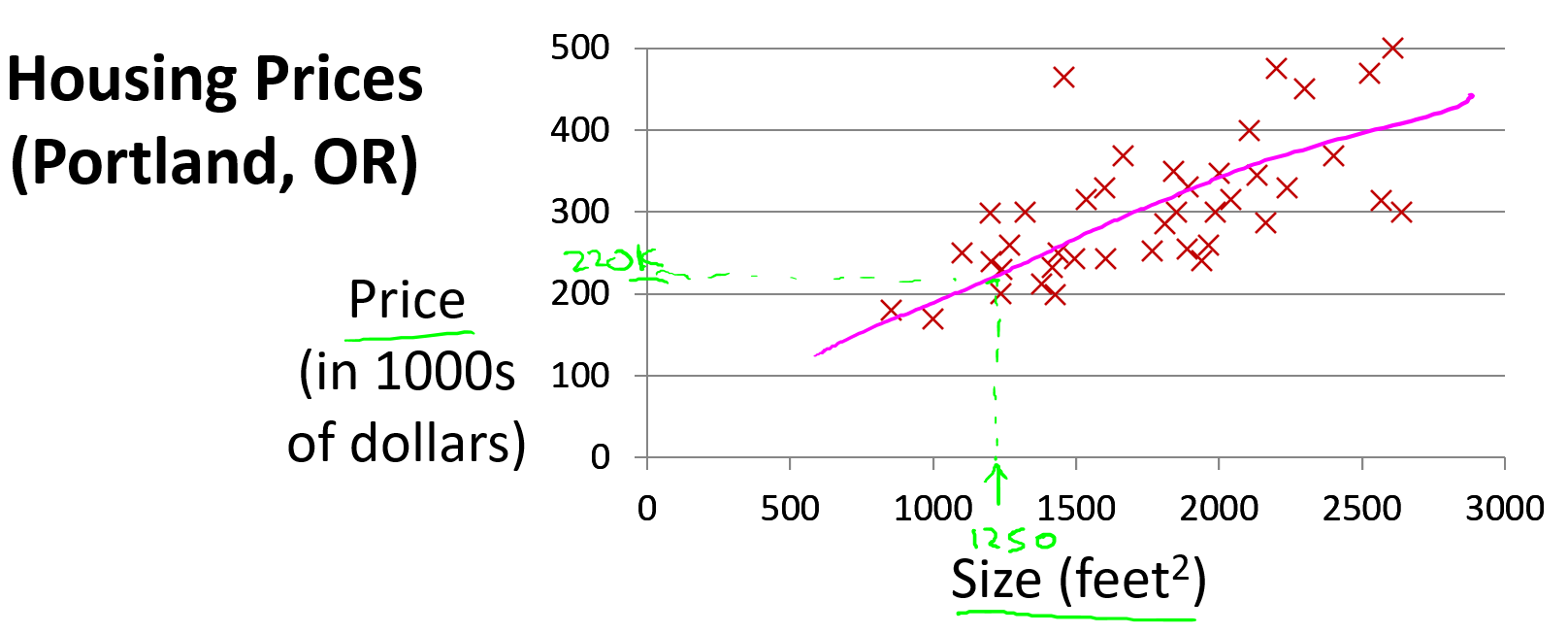
这是监督学习算法的一个例子。 因为在训练过程中,每个数据样本都包含一个“正确答案”,也就是我们已经知道的真实输出(每个房子的实际售价)。而且这还是一个回归问题的例子,因为预测一个具体的数值输出(房子的价格)。
在监督学习中我们有一个数据集,这个数据集被称训练集,如下图。
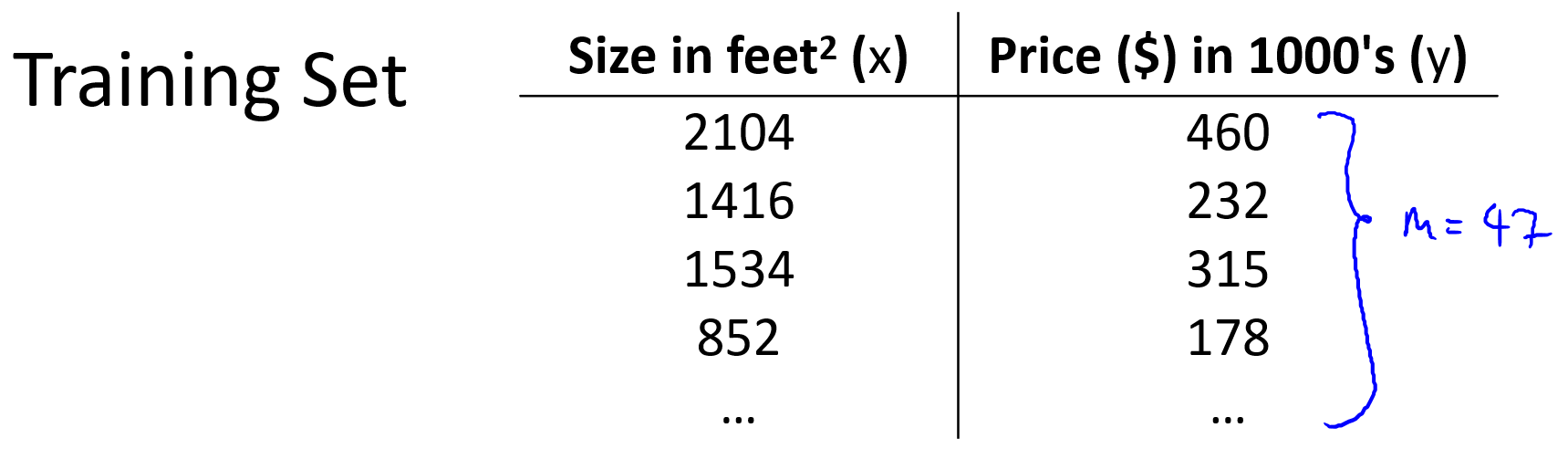
在课程中,使用以下符号来描述训练集和模型结构:
m m m :训练样本数量
x x x :特征/输入变量(例如房子面积)
y y y :目标变量/输出变量(例如房子价格)
( x ( i ) , y ( i ) ) ({{x}^{(i)}},{{y}^{(i)}}) (x(i),y(i)) : 第 i 个训练样本
h h h :学习算法输出的假设函数(hypothesis)
一个典型的监督学习过程如下:

- 收集训练数据,比如不同面积的房子及其对应价格。
- 将这些数据输入给学习算法。
- 算法“学习”出一个函数 h h h,也就是我们的预测模型。
- 当想预测一套房子的售价时,只需将其面积作为输入,使用这个函数 h h h 得到预测价格。
换句话说,我们希望找到一个函数
h
h
h,使得它能近似地预测出输入
x
x
x(房屋面积)对应的输出
y
y
y(价格)。这可以用线性函数表示为:
h
θ
(
x
)
=
θ
0
+
θ
1
x
h_\theta \left( x \right)=\theta_{0} + \theta_{1}x
hθ(x)=θ0+θ1x
因为这里只有一个特征(房子面积),所以我们称这种情况为单变量线性回归。
二、代价函数
在这一节中我们将定义代价函数的概念,这有助于我们弄清楚如何把最有可能的直线与我们的数据相拟合。在上一节中,我们得到的假设函数为一个线性函数形式:
h
θ
(
x
)
=
θ
0
+
θ
1
x
h_\theta \left( x \right)=\theta_{0} + \theta_{1}x
hθ(x)=θ0+θ1x
选择不同的参数 θ 0 \theta_{0} θ0 和 θ 1 \theta_{1} θ1 会得到不同的假设函数 h θ ( x ) h_\theta \left( x \right) hθ(x) ,如下图。

θ i \theta_{i} θi 称为模型参数,我们要做的是选择出一组合适的参数 θ 0 \theta_{0} θ0 和 θ 1 \theta_{1} θ1,使得模型预测值 h θ ( x ) h_\theta \left( x \right) hθ(x) 与实际值 y y y 的差距最小。这里给出标准定义,在线性回归中要解决的是最小化问题。
最小化公式,加平方是为了使差距极其小
min θ 0 , θ 1 ( h θ ( x ) − y ) 2 \min_{\theta_0,\, \theta_1} \quad (h_\theta(x) - y)^2 θ0,θ1min(hθ(x)−y)2
对所有训练样本的差距进行求和, 1 2 m \frac{1}{2m} 2m1 是为了尽量减少平均误差
min θ 0 , θ 1 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 \min_{\theta_0,\, \theta_1} \quad \frac{1}{2m} \sum_{i=1}^{m} \left(h_\theta(x^{(i)}) - y^{(i)}\right)^2 θ0,θ1min2m1i=1∑m(hθ(x(i))−y(i))2
由于假设函数表示为
h θ ( x ( i ) ) = θ 0 + θ 1 x ( i ) h_\theta(x^{(i)}) = \theta_{0} + \theta_{1}x^{(i)} hθ(x(i))=θ0+θ1x(i)
因此问题变成找到 θ 0 \theta_{0} θ0 和 θ 1 \theta_{1} θ1 的值,使以下公式最小
min θ 0 , θ 1 J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 \min_{\theta_0,\, \theta_1} \quad J(\theta_0, \theta_1) = \frac{1}{2m} \sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right)^2 θ0,θ1minJ(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
J ( θ 0 , θ 1 ) J(\theta_0, \theta_1) J(θ0,θ1) 就是代价函数,这个函数也叫作平方误差代价函数,它是回归问题中最常见也是最合理的选择之一。
三、代价函数的直观理解(1)
在这一节中,为了更好地使代价函数J可视化,我们使用一个简化的代价函数,可以让我们更好的理解代价函数的概念。
将假设函数的参数 θ 0 \theta_{0} θ0 视为 0
h θ ( x ( i ) ) = θ 1 x ( i ) h_\theta(x^{(i)}) = \theta_{1}x^{(i)} hθ(x(i))=θ1x(i)
那么代价函数就变为
min θ 1 J ( θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 \min_{\theta_1} \quad J(\theta_1) = \frac{1}{2m} \sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right)^2 θ1minJ(θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
优化目标就是尽量减少 J ( θ 1 ) J(\theta_1) J(θ1) 的值
实际上,有两个关键函数是我们需要去了解的。一个是假设函数 h θ ( x ) h_\theta(x) hθ(x) ,第二个是代价函数 J ( θ 1 ) J(\theta_1) J(θ1) 。假设函数 h h h 是对于给定的 θ 1 \theta_1 θ1 的值,是一个关于 x x x 的函数。代价函数 J J J 是关于参数 θ 1 \theta_1 θ1 的函数。假设有三个点的训练集 ( 1 , 1 ) ( 2 , 2 ) ( 3 , 3 ) (1,1) (2,2) (3,3) (1,1)(2,2)(3,3),当 θ 1 = 1 \theta_1=1 θ1=1 时,代价函数 J J J 的值计算如下。
J ( θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 = 1 2 m ∑ i = 1 m ( θ 1 x ( i ) − y ( i ) ) 2 = 1 2 m ( 0 2 + 0 2 + 0 2 ) = 0 \begin{aligned} J(\theta_1) &= \frac{1}{2m} \sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right)^2 \\ &= \frac{1}{2m} \sum_{i=1}^{m} \left( \theta_{1}x^{(i)} - y^{(i)} \right)^2 \\ &= \frac{1}{2m}(0^2+0^2+0^2) \\ &= 0 \end{aligned} J(θ1)=2m1i=1∑m(hθ(x(i))−y(i))2=2m1i=1∑m(θ1x(i)−y(i))2=2m1(02+02+02)=0
得出当 θ 1 = 1 \theta_1=1 θ1=1 时, h θ ( x ( i ) ) = y ( i ) h_\theta(x^{(i)}) = y^{(i)} hθ(x(i))=y(i) ,因此 J ( 1 ) = 0 J(1) = 0 J(1)=0
绘制的两个函数的图形如下。
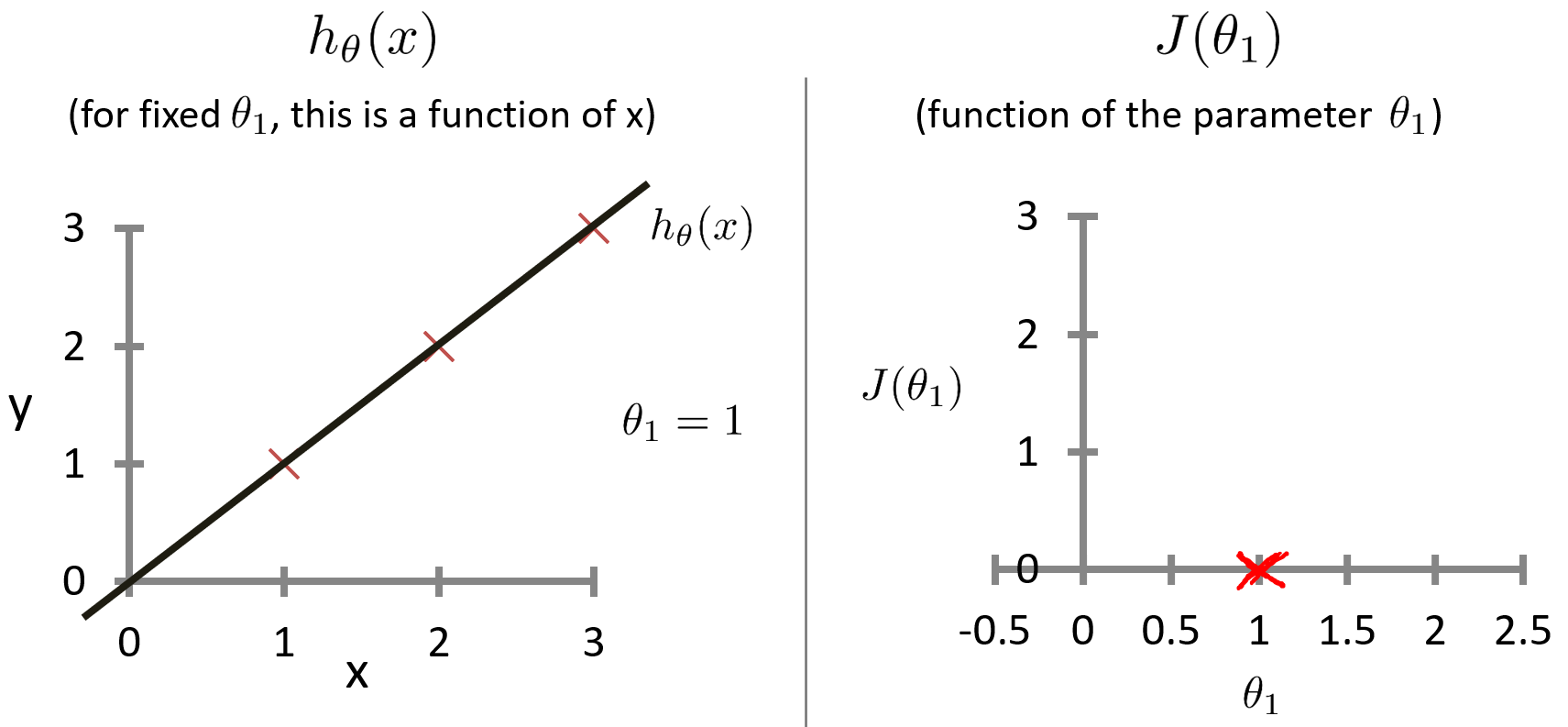
当 θ 1 = 0.5 \theta_1=0.5 θ1=0.5 时,代价函数 J J J 的值计算如下。
J ( θ 1 ) = 1 2 m ∑ i = 1 m ( θ 1 x ( i ) − y ( i ) ) 2 = 1 2 ∗ 3 [ ( 0.5 − 1 ) 2 + ( 1 − 2 ) 2 + ( 1.5 − 3 ) 2 ] ≈ 0.58 \begin{aligned} J(\theta_1) &= \frac{1}{2m} \sum_{i=1}^{m} \left( \theta_{1}x^{(i)} - y^{(i)} \right)^2 \\ &= \frac{1}{2*3}[(0.5-1)^2+(1-2)^2+(1.5-3)^2] \\ &\approx 0.58 \end{aligned} J(θ1)=2m1i=1∑m(θ1x(i)−y(i))2=2∗31[(0.5−1)2+(1−2)2+(1.5−3)2]≈0.58
得出当 θ 1 = 0.5 \theta_1=0.5 θ1=0.5 时, J ( 0.5 ) ≈ 0.58 J(0.5) \approx 0.58 J(0.5)≈0.58
绘制的两个函数的图形如下。

同理,计算出其它代价函数 J J J 的值,比如:
当 θ 1 = 0 \theta_1=0 θ1=0 时, J ( 0 ) ≈ 2.3 J(0) \approx 2.3 J(0)≈2.3
当 θ 1 = − 0.5 \theta_1=-0.5 θ1=−0.5 时, J ( − 0.5 ) ≈ 5.25 J(-0.5) \approx 5.25 J(−0.5)≈5.25
最终,得到的代价函数J的图形如下。
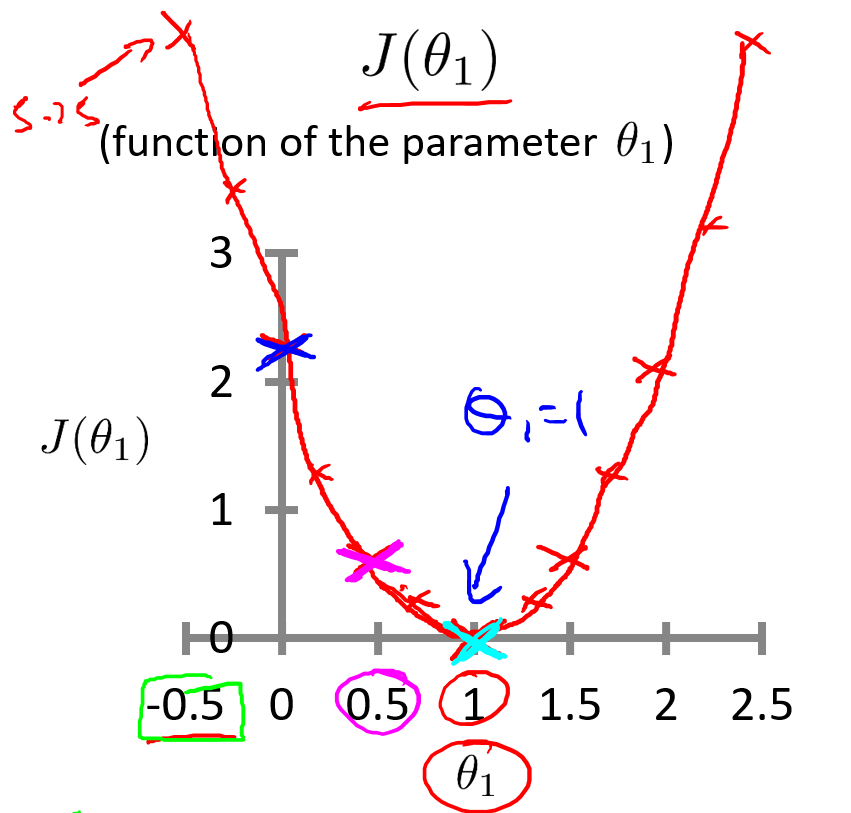
学习算法的优化目标,是通过选择 θ 1 \theta_1 θ1 的值,获得最小的 J ( θ 1 ) J(\theta_1) J(θ1) 。在这条曲线中,当 θ 1 = 1 \theta_1 = 1 θ1=1 时, J ( θ 1 ) J(\theta_1) J(θ1) 最小。通过观察也可以得出,这是条完美拟合训练集数据的直线。
四、代价函数的直观理解(2)
在本节课程中,我们将更深入地学习代价函数的作用,并借助图形化方式(等高线图)来帮助我们直观地理解其行为与最小值位置。下面是本节用到的公式,与上节不一样的是保留参数 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1。
假设函数: h θ ( x ) = θ 0 + θ 1 x h_\theta \left( x \right)=\theta_{0} + \theta_{1}x hθ(x)=θ0+θ1x
模型参数: θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1
代价函数: J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0, \theta_1) = \frac{1}{2m} \sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right)^2 J(θ0,θ1)=2m1∑i=1m(hθ(x(i))−y(i))2
优化目标: min θ 0 , θ 1 J ( θ 0 , θ 1 ) \min_{\theta_0,\, \theta_1} J(\theta_0, \theta_1) minθ0,θ1J(θ0,θ1)
采用关于住房价格的训练集,假设 θ 0 = 50 , θ 1 = 0.06 \theta_0=50,\theta_1=0.06 θ0=50,θ1=0.06,绘制假设函数h和代价函数 J J J 的图形。其中,代价函数 J J J 是关于 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 的函数,是一个3D曲面图,横轴为 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 ,竖轴为代价函数 J J J。
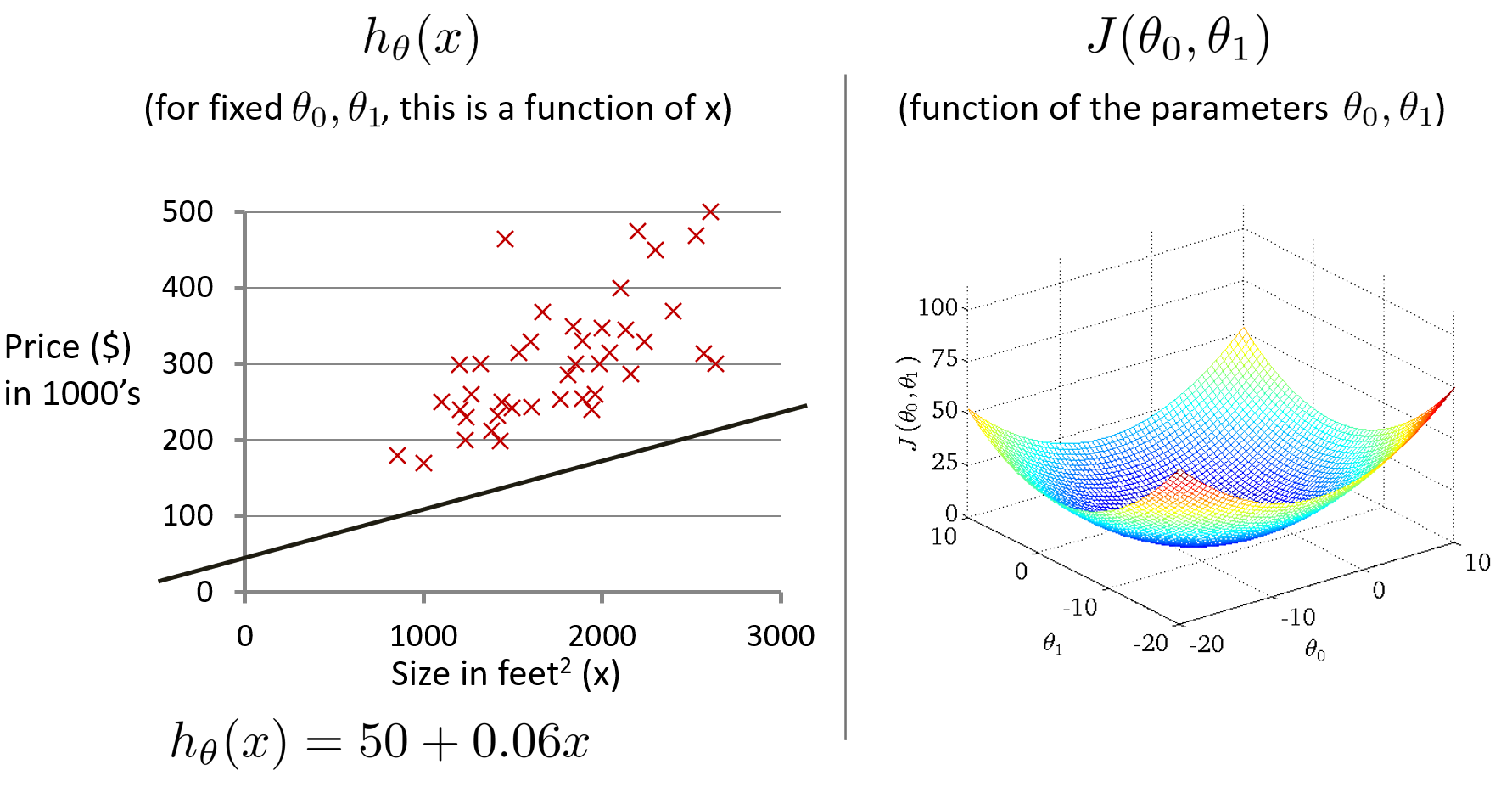
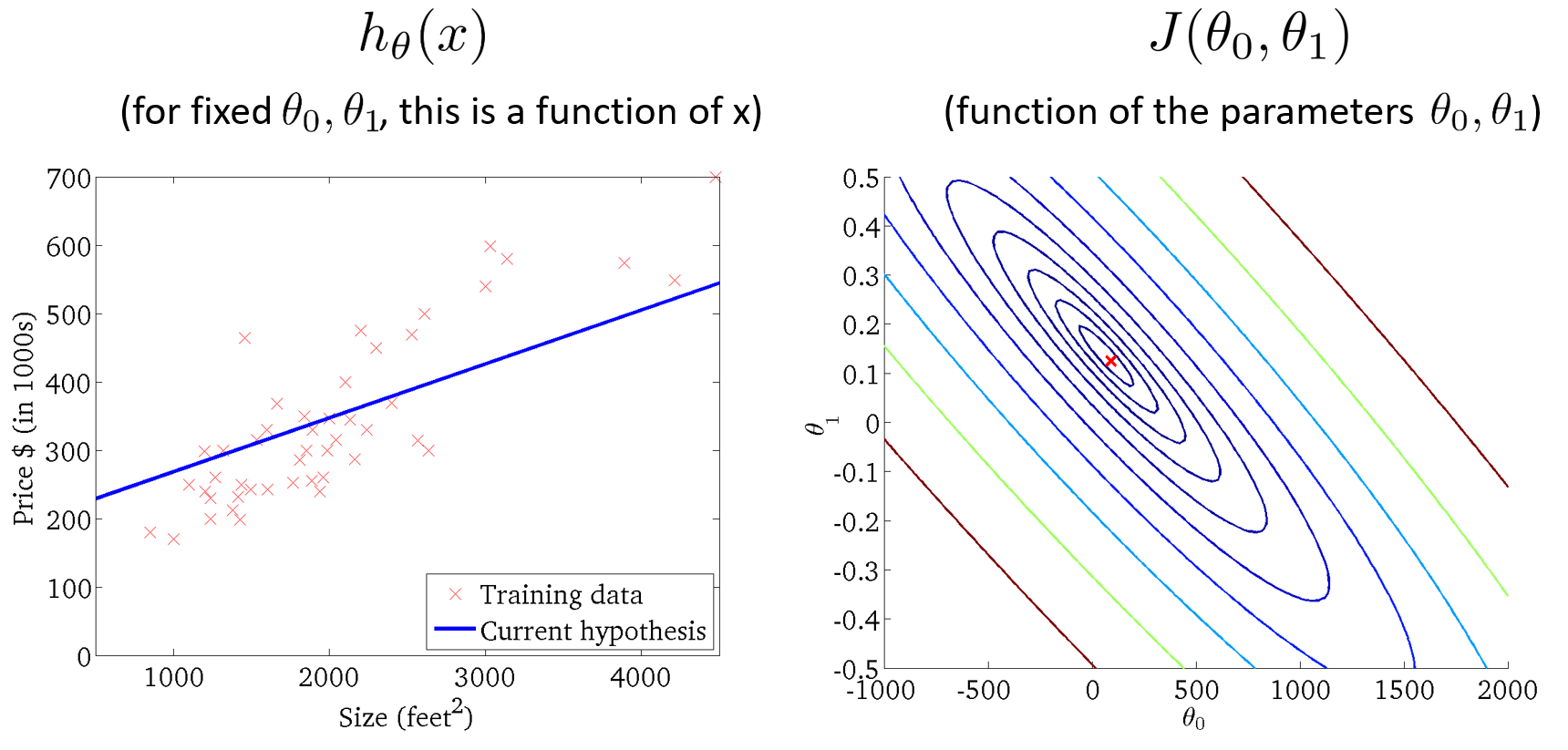
为了更好地展现图形, 我们使用等高线图来展示代价函数,轴为 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 ,每个椭圆形显示一系列 J ( θ 0 , θ 1 ) J(\theta_0, \theta_1) J(θ0,θ1) 值相等的点,这些同心椭圆的中心点是代价函数的最小值。右下图是代价函数的等高线图,左下图是代价函数的最小值(椭圆的中心点)对应的假设函数的图形。
五、梯度下降
在本节课程中,我们将使用梯度下降法替代在上节中的人工方法,来自动寻找代价函数 J J J 最小值对应的参数 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 ,也更适合处理在遇到更复杂、更高维度、更多参数的难以可视化的情况。
问题概述:假设有个代价函数 J ( θ 0 , θ 1 ) J(\theta_0, \theta_1) J(θ0,θ1) ,我们需要用一个算法来最小化这个代价函数。
梯度下降法的思路:首先给定 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 的初始值,通常为 θ 0 = 0 , θ 1 = 0 \theta_0=0,\theta_1=0 θ0=0,θ1=0 ,然后不停地一点点地改变 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 的值来使 J J J 变小,直到找到 J J J 的最小值或局部最小值。
通过图像可以更直观地理解梯度下降法是如何最小化代价函数 J J J 的。下图是横轴为 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 ,竖轴为代价函数 J J J ,并对 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 赋以不同的初始值。

把这个图像想象为公园中的两座山,然后你正站在山上的一个点上,在梯度下降算法中,我们要做的就是旋转 360度,看看周围,并问自己要尽快下山的话,我应该朝什么方向迈步?然后你按照自己的判断迈出一步,重复上面的步骤,从这个新的点,你环顾四周,并决定从什么方向将会最快下山,然后又迈进了一小步,并依此类推,直到你接近局部最低点的位置。对 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 赋以不同的初始值,会得到如图中两个不同的局部最低点,这是梯度下降法的一个特点。
如下图是梯度下降法的数学定义,将会重复更新 θ j \theta_j θj 的步骤,直到收敛。

其中是 α α α 学习率,用来控制梯度下降时迈出的步子有多大。如果 α α α 值很大,会用大步子下山,梯度下降就很迅速;如果 α α α 值很小,会迈着小碎步下山,梯度下降就很慢。 ∂ ∂ θ j J ( θ 0 , θ 1 ) \frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1) ∂θj∂J(θ0,θ1) 是代价函数 J J J 的导数,这跟微积分有关系。
要正确实现梯度下降法,还需要同时更新 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 ,左下图的同时更新是正确的,右下图没有同时更新是错误的。

六、梯度下降的直观理解
梯度下降算法的数学定义如下,其中, α α α 是学习率, ∂ ∂ θ j J ( θ 0 , θ 1 ) \frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1) ∂θj∂J(θ0,θ1) 是导数项。本节课程将直观认识这两部分的作用,以及更新过程有什么意义。

下面将直观解释导数项的意义,如下图像,是一个只有参数 θ 1 \theta_1 θ1 的简化的代价函数 J ( θ 1 ) J(\theta_1) J(θ1) 的图像,梯度下降算法的更新规则: θ 1 : = θ 1 − α ∂ ∂ θ 1 J ( θ 1 ) \theta_1:=\theta_1-\alpha\frac{\partial}{\partial \theta_1} J(\theta_1) θ1:=θ1−α∂θ1∂J(θ1)

导数项 ∂ ∂ θ 1 J ( θ 1 ) \frac{\partial}{\partial \theta_1} J(\theta_1) ∂θ1∂J(θ1) 可以说是 θ 1 \theta_1 θ1 点关于代价函数 J ( θ 1 ) J(\theta_1) J(θ1) 的切线的斜率,斜率可以表示 k = t a n β k=tan\beta k=tanβ 其中, β β β 是直线与 x x x 轴正方向的夹角。因此,图中是个正斜率,也就是正导数,同时学习率 α α α 永远是个正数,所以 θ 1 \theta_1 θ1 更新后变小了,要往左移,更接近最低点。

取另一个点 θ 1 \theta_1 θ1 ,如上图,计算得出是负斜率,也就是负导数,所以 θ 1 \theta_1 θ1 更新后变大了,要往右移,更接近最低点。
接下来介绍学习率 α α α 的作用,如果 α α α 太小,如下图,结果就是会一点点地挪动,需要很多步才能到达全局最低点。
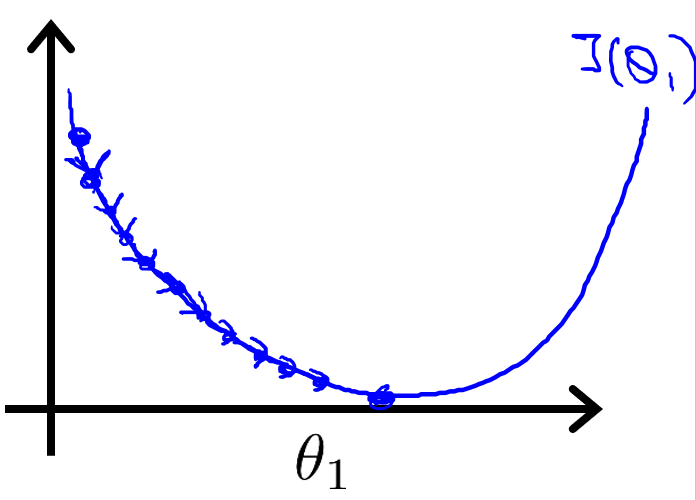
如果 α α α 太大,如下图,那么梯度下降法可能会越过最低点,甚至可能无法收敛或者发散。
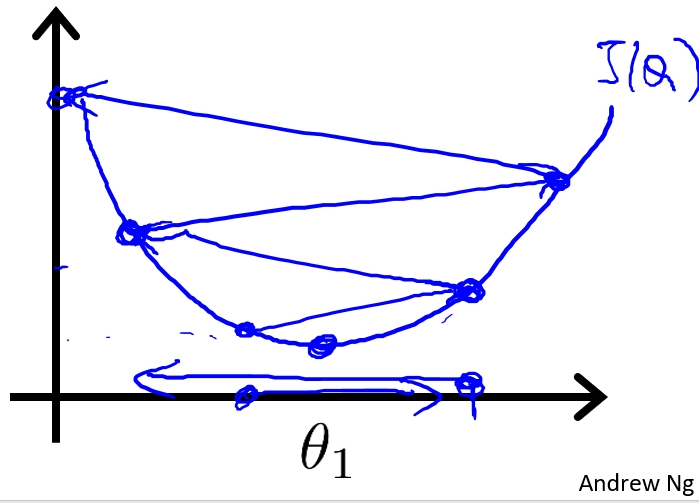
如果 θ 1 \theta_1 θ1 已经处在一个局部的最低点,如下图,由于最低点的斜率为 0,也就是导数等于 0,所以 θ 1 \theta_1 θ1 将保持不变,那么梯度下降法更新其实什么都没做,它不会改变参数的值。

接下来解释即使学习速率 α α α 保持不变时,梯度下降也可以收敛到局部最低点。如下图,在梯度下降法的更新过程中,随着越接近最低点,导数(斜率)越来越小,梯度下降将自动采取较小的幅度, θ 1 \theta_1 θ1 更新的幅度就会越小,直到收敛到局部极小值,这就是梯度下降的做法。所以实际上没有必要再另外减小 α α α 。

七、线性回归的梯度下降
在本节课程,我们要将梯度下降法和代价函数结合,得到线性回归的算法,它可以用直线模型来拟合数据。如下图,是梯度下降算法和线性回归模型,线性回归模型包含了假设函数和平方差代价函数。

将梯度下降法和代价函数结合,即最小化平方差代价函数,关键在于求出代价函数的导数
∂ ∂ θ j J ( θ 0 , θ 1 ) = ∂ ∂ θ j 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 = ∂ ∂ θ j 1 2 m ∑ i = 1 m ( θ 0 + θ 1 x ( i ) − y ( i ) ) 2 \begin{aligned} \frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1) &= \frac{\partial}{\partial \theta_j}\frac{1}{2m} \sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right)^2 \\ &= \frac{\partial}{\partial \theta_j}\frac{1}{2m} \sum_{i=1}^{m} \left( \theta_{0} + \theta_{1}x^{(i)} - y^{(i)} \right)^2\end{aligned} ∂θj∂J(θ0,θ1)=∂θj∂2m1i=1∑m(hθ(x(i))−y(i))2=∂θj∂2m1i=1∑m(θ0+θ1x(i)−y(i))2
根据微积分公式,在 j j j 等于0和1时,推导出的偏导数公式如下
∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( θ 0 + θ 1 x ( i ) − y ( i ) ) \frac{\partial}{\partial \theta_0} J(\theta_0, \theta_1) = \frac{1}{m} \sum_{i=1}^{m} \left( \theta_{0} + \theta_{1}x^{(i)} - y^{(i)} \right) ∂θ0∂J(θ0,θ1)=m1∑i=1m(θ0+θ1x(i)−y(i))
∂ ∂ θ 1 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( ( θ 0 + θ 1 x ( i ) − y ( i ) ) ∗ x ( i ) ) \frac{\partial}{\partial \theta_1} J(\theta_0, \theta_1) = \frac{1}{m} \sum_{i=1}^{m} \left(( \theta_{0} + \theta_{1}x^{(i)} - y^{(i)} )*x^{(i)}\right) ∂θ1∂J(θ0,θ1)=m1∑i=1m((θ0+θ1x(i)−y(i))∗x(i))
根据公式计算出偏导数项的值,就可以代入到梯度下降法中,不断地对参数进行同步更新,直到收敛,得到线性回归的全局最优解。

在上面的算法中,有时也称为“批量梯度下降”,指的是在梯度下降的每一步中,我们都用到了所有的训练样本。在梯度下降中,在计算微分求导项时,我们需要进行求和运算,需要对所有
m
m
m 个训练样本求和。而事实上,有时也有其他类型的梯度下降法,不是这种"批量"型的,不考虑整个的训练集,而是每次只关注训练集中的一些小的子集。
如果之前有学过高等线性代数,应该知道有一种计算代价函数 J J J 最小值的解法,而不需要使用梯度下降这种迭代算法。这是另一种称为正规方程(normal equations)的方法。实际上在数据量较大的情况下,梯度下降法比正规方程要更适用一些。
八、代码实现
下面以 Coursera 上的一元线性回归数据集 ex1data1.txt 为例实现代码:
import numpy as np
import matplotlib.pyplot as plt
# load data, data.shape = (97, 2)
data = np.loadtxt('ex1data1.txt', delimiter=',', usecols=(0, 1))
x = data[:, 0]
y = data[:, 1]
m = y.size
# parameters
alpha = 0.01
num_iters = 5000
theta = np.zeros(2)
# X.shape = (97, 2), y.shape = (97, ), theta.shape = (2, )
X = np.c_[np.ones(m), x] # 增加一列 1 到 矩阵 X,实现多项式运算
# Gradient Descent
for _ in range(0, num_iters):
error = (X @ theta).flatten() - y # error.shape = (97, )
theta -= (alpha / m) * np.sum(X * error[:, np.newaxis], 0) # 0 表示每列相加
# plot
print(theta)
plt.scatter(x, y)
x_plot = np.array([np.min(x), np.max(x)])
y_plot = theta[0] + x_plot * theta[1] # NumPy Broadcast
plt.plot(x_plot, y_plot, c="m")
plt.show()
得到的 ( θ 0 , θ 1 ) (\theta_0, \theta_1) (θ0,θ1) 结果是: [ − 3.8953 , 1.1929 ] [-3.8953, 1.1929] [−3.8953,1.1929],作图如下:

向量化:在 Python 或 Matlab 中进行科学计算时,如果有多组数据或多项式运算,转化成矩阵乘法会比直接用 for 循环高效很多,可以实现同时赋值且代码更简洁。
这是由于科学计算库中的函数更好地利用了硬件的特性,更好地支持了诸如循环展开、流水线、超标量等技术。






















 335
335

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








