鲁老师深度学习笔记（1）—最大似然估计

最大似然估计是机器学习中最常用的参数估计方法之一。整个建模过程需要一个似然函数来描述在不同模型参数下真实数据发生的概率，似然函数是关于模型参数的函数。最大似然估计就是寻找最优参数，使得观测数据发生的概率最大、统计模型与真实数据最相似。

对于一组训练数据，使用线性回归建模，可以有不同的模型参数来描述数据，这时候可以用最小二乘法来选择最优参数来拟合训练数据，即使用误差的平方作为损失函数。机器学习求解参数的过程被称为参数估计，机器学习问题也变成求使损失函数最小的最优化问题。最小二乘法比较直观，很容易解释，但不具有普遍意义，对于更多其他机器学习问题，比如二分类和多分类问题，最小二乘法就难以派上用场了。本文将给大家介绍一个具有普遍意义的参数估计方法：最大似然估计。

我们以一个赌博的例子来模拟机器学习的概率推理过程。假如你参与了一场赌博，你会被告知一个硬币抛掷10次的正反情况，接下来由你下注，而你只有一次机会，猜对硬币下一次正反情况则赢得100元，猜错则损失100元。这时，你会如何决策？

一、概率和似然

一般地，硬币有正反两面，如果硬币正反两面是均匀的，即每次抛掷后硬币为正的概率是0.5。使用这个硬币，很可能抛10次，有5次是正面。但是假如有人对硬币做了手脚，比如提前对硬币做了修改，硬币每次都会正面朝上，现在抛10次，10次都是正面，那么下次你绝对不会猜它是反面，因为前面的10次结果摆在那里，直觉上你不会相信这是一个普通的硬币。现在有一人抛了10次硬币，得到6正4反的结果，如何估算下次硬币为正的概率呢？

因为硬币并不是我们制作的，我们不了解硬币是否是完全均匀的，只能根据现在的观察结果来反推硬币的情况。假设硬币上有个参数 $\theta$，它决定了硬币的正反均匀程度，$\theta =0.5$ 表示正反均匀，每次抛硬币为正的概率为 0.5，$\theta =1$ 表示硬币只有正面，每次抛硬币为正的概率为 1。那么，从观察到的正反结果，反推硬币的构造参数 $\theta$ 的过程，就是一个参数估计的过程。

1、概率

抛掷10次硬币可能出现不同的情况，可以是“5正5反”、“4正6反”，“10正0反”等。假如我们知道硬币是如何构造的，即已知硬币的参数 $\theta$，通过二项分布公式计算出现“6正4反”的概率为：
$$\begin{array}{rl}P(6H4T\mid \theta =0.5)& ={\mathrm{C}}_{10}^6\times 0.5^6\times (1-0.5{)}^4\approx 0.2051\\ P(6H4T\mid \theta =0.6)& ={\mathrm{C}}_{10}^6\times 0.6^6\times (1-0.6{)}^4\approx 0.2508\\ P(6H4T\mid \theta =0.9)& ={\mathrm{C}}_{10}^6\times 0.9^6\times (1-0.9{)}^4\approx 0.0112\end{array}$$

上面这个公式是概率函数，表示已知参数 $\theta$，事实“6正4反”发生的概率，H(Heads)表示正面，T(Tails)表示反面。参数 $\theta$ 取不同的值时，事情发生的概率不同。在数学上一般使用 $P$ 表示概率（Probability）函数。

上述过程中，抛10次硬币，要选出6次正面，使用了排列组合。因为“6正4反”可能会出现正正正正正正反反反反、正正正正正反正反反反、正正正正反正正反反反等共210种组合，要在10次中选出6次为正面。假如每次正面的概率是0.6，那么反面的概率就是(1-0.6)。每次抛掷硬币的动作是相互独立，互不影响的，“6正4反”发生的概率就是各次抛掷硬币的概率乘积，再乘以210种组合。

概率反映的是：已知背后原因，推测某个结果发生的概率。

2、似然

与概率不同，似然反映的是：已知结果，反推原因。具体而言，似然（Likelihood）函数表示的是基于观察的数据，取不同的参数 $\theta$ 时，统计模型以多大的可能性接近真实观察数据。这就很像开篇提到的赌局，已经给你了一系列硬币正反情况，但你并不知道硬币的构造，下次下注时你要根据已有事实，反推硬币的构造。例如，当观察到硬币“10正0反”的事实，猜测硬币极有可能每次都是正面；当观察到硬币“6正4反”的事实，猜测硬币有可能不是正反均匀的，每次出现正面的可能性是0.6。

似然函数与前面的概率函数的计算方式极其相似，与概率函数不同的是，似然函数是 $\theta$ 的函数，即 $\theta$ 是未知的。似然函数衡量的是在不同参数 $\theta$ 下，真实观察数据发生的可能性。似然函数通常是多个观测数据发生的概率的联合概率，即多个观测数据都发生的概率。在机器学习里可以这样理解，目标 y 和特征 x 同时发生，这些数值被观测到的概率。单个观测数据发生的可能性为 $P(\theta )$ ，如果各个观测之间是相互独立的，那么多个观测数据都发生的概率可表示为各个样本发生的概率的乘积。

这里稍微解释一下事件独立性与联合概率之间的关系。如果事件A和事件B相互独立，那么事件A和B同时发生的概率是 $P(A)\times P(B)$ 。例如，事件“下雨”与事件“地面湿”就不是相互独立的，“下雨”与"地面湿"是同时发生、高度相关的，这两个事件都发生的概率就不能用概率的乘积来表示。两次抛掷硬币相互之间不影响，因此硬币正面朝上的概率可以用各次概率的乘积来表示。

似然函数通常用 L 表示，对应英文 Likelihood。观察到抛硬币“6正4反”的事实，硬币参数 $\theta$ 取不同值时，似然函数表示为：
$$L(\theta ;6H4T)={\mathrm{C}}_{10}^6\times {\theta }^6\times (1-\theta {)}^4$$

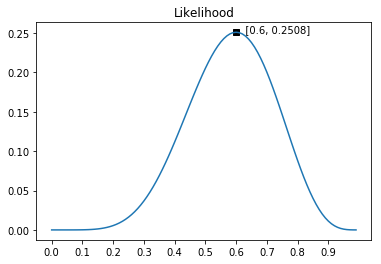
这个公式的图形如下图所示。从图中可以看出：参数 $\theta$ 为0.6时，似然函数最大，参数为其他值时，“6正4反”发生的概率都相对更小。在这个赌局中，我会猜测下次硬币为正，因为根据已有观察，硬币很可能以0.6的概率为正。

“6正4反”的似然函数

推广到更为一般的场景，似然函数的一般形式可以用下面公式来表示，也就是之前提到的，各个样本发生的概率的乘积。
$$L(\theta ;\mathbf{X})=P_1(\theta ;X_1)\times P_2(\theta ;X_2)\cdots \times P_n(\theta ;X_n)=\prod P_i(\theta ;X_i)$$

本文公式中变量加粗表示该变量为向量或矩阵

二、最大似然估计

理解了似然函数的含义，就很容易理解最大似然估计的机制。似然函数是关于模型参数的函数，是描述观察到的真实数据在不同参数下发生的概率。最大似然估计要寻找最优参数，让似然函数最大化。或者说，使用最优参数时观测数据发生的概率最大。

1、线性回归的最大似然估计

线性回归的误差项 $ϵ$ 是预测值与真实值之间的差异，如下面公式所示。它可能是一些随机噪音，也可能是线性回归模型没考虑到的一些其他影响因素。
$$y^{(i)}={ϵ}^{(i)}+\sum _{j=1}^n{w}_j{x}_j^{(i)}={ϵ}^{(i)}+{\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}$$

线性回归的一大假设是：误差服从均值为 0 的正态分布，且多个观测数据之间互不影响，相互独立。正态分布（高斯分布）的概率密度公式如下面公式，根据正态分布的公式，可以得到 $ϵ$ 的概率密度。

假设 $x$ 服从正态分布，它的均值为 $\mu$，方差为 $\sigma$，它的概率密度公式如下。公式左侧的 $P(x;\mu ,\sigma )$ 表示 $x$ 是随机变量，;分号强调 $\mu$ 和 $\sigma$ 不是随机变量，而是这个概率密度函数的参数。条件概率函数中使用的 | 竖线有明确的意义，$P(y|x)$ 表示给定 $x，y$ 发生的概率。
$$P(x;\mu ,\sigma )=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)$$

既然误差项服从正态分布，那么：
$$P({ϵ}^{(i)})=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{({ϵ}^{(i)}{)}^2}{2{\sigma }^2}\right)$$

由于 ${ϵ}^{(i)}=y^{(i)}-{\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}$ ，并取均值 $\mu$ 为0，可得到：
$$P(y^{(i)}\mid {\mathbf{x}}^{(i)};\mathbf{w})=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{(y^{(i)}-{\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}{)}^2}{2{\sigma }^2}\right)$$

上式表示给定 $x^{(i)},y^{(i)}$ 的概率分布。$\mathbf{w}$ 并不是随机变量，而是一个参数，所以用;分号隔开。或者说 $\mathbf{w}$ 和 ${\mathbf{x}}^{(i)}$ 不是同一类变量，需要分开单独理解。$P(y^{(i)}|{\mathbf{x}}^{(i)},\mathbf{w})$ 则有完全不同的意义，表示 ${\mathbf{x}}^{(i)}$ 和 $\mathbf{w}$ 同时发生时，$y^{(i)}$ 的概率分布。

前文提到，似然函数是所观察到的各个样本发生的概率的乘积。一组样本有 $m$ 个观测数据，其中单个观测数据发生的概率为刚刚得到的公式，$m$ 个观测数据的乘积如下所示。
$$L(\mathbf{w})=L(\mathbf{w};\mathbf{X},\mathbf{y})=\prod _{i=1}^{m}P(y^{(i)}\mid {\mathbf{x}}^{(i)};\mathbf{w})$$

最终，似然函数可以表示成：
$$L(\mathbf{w})=\prod _{i=1}^m\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{(y^{(i)}-{\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}{)}^2}{2{\sigma }^2}\right)$$

其中，$x^{(i)}$ 和 $y^{(i)}$ 都是观测到的真实数据，是已知的，$\mathbf{w}$ 是需要去求解的模型参数。

给定一组观测数据 $\mathbf{x}$ 和 $\mathbf{y}$，如何选择参数 $\mathbf{w}$ 来使模型达到最优的效果？最大似然估计法告诉我们应该选择一个 $\mathbf{w}$ ，使得似然函数 $L$ 最大。$L$ 中的乘积符号和 $exp$ 运算看起来就非常复杂，直接用 $L$ 来计算十分不太方便，于是统计学家在原来的似然函数基础上，取了 $log$⁡ 对数。 $log$ 的一些性质能大大化简计算复杂程度，且对原来的似然函数增加 $log$ 对数并不影响参数 $\mathbf{w}$ 的最优值。通常使用花体的 $\ell$ 来表示损失函数的对数似然函数。
$$\begin{array}{rl}\ell (\mathbf{w})& =\log L(\mathbf{w})\\ & =\log \prod _{i=1}^m\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{(y^{(i)}-{\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}{)}^2}{2{\sigma }^2}\right)\\ & =\sum _{i=1}^m\log \left[\frac{1}{\sqrt{2\pi {\sigma }^2}}\cdot \exp \left(-\frac{(y^{(i)}-{\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}{)}^2}{2{\sigma }^2}\right)\right]\\ & =\sum _{i=1}^m\log \left[\frac{1}{\sqrt{2\pi {\sigma }^2}}\right]+\sum _{i=1}^m\log \left[\exp \left(-\frac{(y^{(i)}-{\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}{)}^2}{2{\sigma }^2}\right)\right]\\ & =m\log \frac{1}{\sqrt{2\pi {\sigma }^2}}-\frac{1}{2{\sigma }^2}\sum _{i=1}^m(y^{(i)}-{\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}{)}^2\end{array}$$

上面的推导过程主要利用了下面两个公式：
$$\begin{array}{r}\log (ab)=\log (a)+\log (b)\\ {\log }_e(\exp (a))=a\end{array}$$

由于 $log$ ⁡对数可以把乘法转换为加法，似然函数中的乘积项变成了求和项。又因为 $log$ ⁡对数可以消去幂，最终可以得到上述结果。

由于我们只关心参数 $\mathbf{w}$ 取何值时，似然函数最大，标准差 $\sigma$ 并不会影响 $\mathbf{w}$ 取何值时似然函数最大，所以可以忽略掉带有标准差 $\sigma$ 的项 $m\log \frac{1}{\sqrt{2\pi {\sigma }^2}}$。再在 $-\frac{1}{2{\sigma }^2}{\sum }_{i=1}^m(y^{(i)}-{\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}{)}^2$ 加个负号，负负得正，原来似然函数 $\ell$ 最大化问题就变成了最小化问题，其实最后还是最小化：
$$\sum _{i=1}^m(y^{(i)}-{\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}{)}^2$$

这与最小二乘法所优化的损失函数几乎一样，都是“真实值 - 预测值”的平方和，可以说是殊途同归。直观上来说，最小二乘法是在寻找观测数据与回归超平面之间的误差距离最小的参数。最大似然估计是最大化观测数据发生的概率。当我们假设误差是正态分布的，所有误差项越接近均值 0，概率越大。正态分布是在均值两侧对称的，误差项接近均值的过程等同于距离最小化的过程。

2、逻辑回归的最大似然估计

用概率解释预测值
$$P(y=k)=\{\begin{array}{ll}p& k=1\\ 1-p& k=0\end{array}$$

利用「伯努利分布公式」故：
P ( y = k ) = [ h θ ( x ) ] k [ 1 − h θ ( x ) ] 1 − k , k ∈ { 0 , 1 } P(y = k) = \left[ h_\theta(x) \right]^k \left[ 1 - h_\theta(x) \right]^{1 - k}, \quad k \in \{0, 1\} P(y=k)=[hθ​(x)]k[1−hθ​(x)]1−k,k∈{0,1}

​
而对于数据集 $\left\{(x^{(i)},y^{(i)}),i=1,2,\cdots ,m\right\}$ 下，将其视为已发生的一个事件组，则似然函数为：
$$L(\theta )=\prod _{i=1}^{m}P\left(y=y^{(i)}\right)=\prod _{i=1}^m{\left[h_{\theta }\left(x^{(i)}\right)\right]}^{y^{(i)}}{\left[1-h_{\theta }\left(x^{(i)}\right)\right]}^{1-y^{(i)}}$$

取对数得到：
$$\ln L(\theta )=\sum _{i=1}^m\left\{y^{(i)}\ln \left[h_{\theta }\left(x^{(i)}\right)\right]+\left(1-y^{(i)}\right)\ln \left[1-h_{\theta }\left(x^{(i)}\right)\right]\right\}$$

​
注意到，最大似然估计法的目标是找到 $L(\theta )$ 或 $\ln L(\theta )$ 的最大值，而逻辑回归的目标是找到 $J(\theta )$ 的最小值，所以自然的，我们将 $\ln L(\theta )$ 取反来定义 $J(\theta )$ ：
$$\begin{array}{rl}J(\theta )& =-\frac{1}{m}\ln L(\theta )\\ & =-\frac{1}{m}\sum _{i=1}^m\left[y^{(i)}\ln \left(h_{\theta }\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right)\ln \left(1-h_{\theta }\left(x^{(i)}\right)\right)\right]\end{array}$$

​
其中 $\frac{1}{m}$ 对要求的 $\theta$ 没有影响，仅是取一下平均罢了。

可以证明上述代价函数 $J(\theta )$ 会是一个凸函数，并且没有局部最优值。凸性分析的内容不在本讲的范围，但是可以证明我们所选的代价函数会给我们带来一个凸优化问题。

既然是凸函数，那么现在我们就可以进行梯度下降求解 $\arg {\min }_{\theta }J(\theta )$

利用 sigmoid 函数的对数性质 $\log \sigma (z)=-\log (1+e^{-z})$ 和 $\log (1-\sigma (z))=-\log (1+e^z)$

求偏导，我们先计算：
$$\begin{array}{rl}\frac{\partial }{\partial \theta }\text{Cost}\left(h_{\theta }(x),y\right)& =\frac{\partial }{\partial \theta }\left[-y\ln \left(h_{\theta }(x)\right)-(1-y)\ln \left(1-h_{\theta }(x)\right)\right]\\ & =\frac{\partial }{\partial \theta }\left[y\ln \left(1+e^{-{\theta }^{T}x}\right)+(1-y)\ln \left(1+e^{{\theta }^{T}x}\right)\right]\\ & =\frac{-yx{e}^{-{\theta }^{T}x}}{1+e^{-{\theta }^{T}x}}+\frac{(1-y)x{e}^{{\theta }^{T}x}}{1+e^{{\theta }^{T}x}}\\ & =\frac{-yx+(1-y)x{e}^{{\theta }^{T}x}}{1+e^{{\theta }^{T}x}}\\ & =\left(-y+\frac{1}{1+e^{-{\theta }^{T}x}}\right)x\\ & =\left(h_{\theta }(x)-y\right)x\end{array}$$

于是乎，
$$\frac{\partial J}{\partial \theta }=\frac{1}{m}\sum _{i=1}^m\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)x^{(i)}$$

​
没错，这个偏导的形式和线性回归完全相同！不同的只是 $h_{\theta }(x)=g\left({\theta }^{T}X\right)$ 的定义——多了一层 sigmoid 函数，正是因此，我们不能使用正规方程直接给出解析解，而必须使用梯度下降等方法。

三、总结

最大似然估计是机器学习中最常用的参数估计方法之一，逻辑回归、深度神经网络等模型都会使用最大似然估计。我们需要一个似然函数来描述真实数据在不同模型参数下发生的概率，似然函数是关于模型参数的函数。最大似然估计就是寻找最优参数，使得观测数据发生的概率最大、统计模型与真实数据最相似。

​

​

​

​

​