非递归访问一颗二叉树【C++】

最新推荐文章于 2026-01-02 10:17:02 发布

原创最新推荐文章于 2026-01-02 10:17:02 发布 · 144 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

本文详细介绍了如何使用非递归方法遍历二叉树，包括前序、中序和后序遍历，通过栈的数据结构实现了对每个节点的访问策略。

非递归访问一颗二叉树：

1.左路节点

2.左路节点的右子树

3.子问题访问右树

144. 二叉树的前序遍历 - 力扣（LeetCode）

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        TreeNode* cur = root;
        vector<int> v;
        while(cur||!st.empty())
        {
            //开始访问一棵树
            //1.左路节点
            //2.左路节点的右子树
            while(cur)
            {
                v.push_back(cur->val);
                st.push(cur);
                cur = cur->left;
            }
            //开始访问右子树
            TreeNode* top = st.top();
            st.pop();
            //子问题访问右树
            cur=top->right;
        }
        return v;
    }
};

94. 二叉树的中序遍历 - 力扣（LeetCode）

与上述思路相同。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while(cur||!st.empty())
        {
            //左路节点
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }
            //栈里面取到左路节点，左路节点他左子树访问完了
            TreeNode* top = st.top();
            st.pop();
            v.push_back(top->val);
            //访问左路节点右子树 -- 子问题
            cur = top->right;
        }
        return v;
    }
};

145. 二叉树的后序遍历 - 力扣（LeetCode）

/**
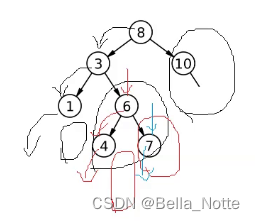
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack <TreeNode*> st;
        vector<int> v;
        TreeNode* cur = root;
        TreeNode* prev = NULL;
        while(cur||!st.empty())
        {
            //1.左路节点
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }
            ///栈里面取到左路节点。左路节点他左子树访问完了。
            TreeNode* top = st.top();
            //1.右为空，或者右子树已经访问过了（上一个访问的节点是右子树的根），可以访问根节点
            if(top->right == nullptr||top->right == prev)
            {
                v.push_back(top->val);
                st.pop();
                prev = top;
            }
            else
            {
                //访问左路节点右子树 -- 子问题
                cur = top->right;
            }
        }
        return v;
    }
};