用Python绘制超炫酷动态莫比乌斯环：数学与编程的完美结合

本文将带您用Python代码实现一个令人惊艳的动态莫比乌斯环，结合三维可视化与动画效果，展现数学之美与编程魔法的碰撞。通过参数方程实现空间扭曲，运用Matplotlib打造流动的渐变色与视角旋转效果，最终呈现出一个仿佛来自异次元的动态曲面。（效果图见文末）

---

一、效果预览

最终实现效果：

• 动态背景：背景颜色随时间变化，呈现出动态的渐变效果。
• 动态透明度：莫比乌斯带的透明度随时间波动，增加了视觉层次感。
• 动态颜色映射：颜色映射随时间变化，增强了动画的炫酷效果。
• 动态视角：视角不断旋转，增加了动画的动态感。

---

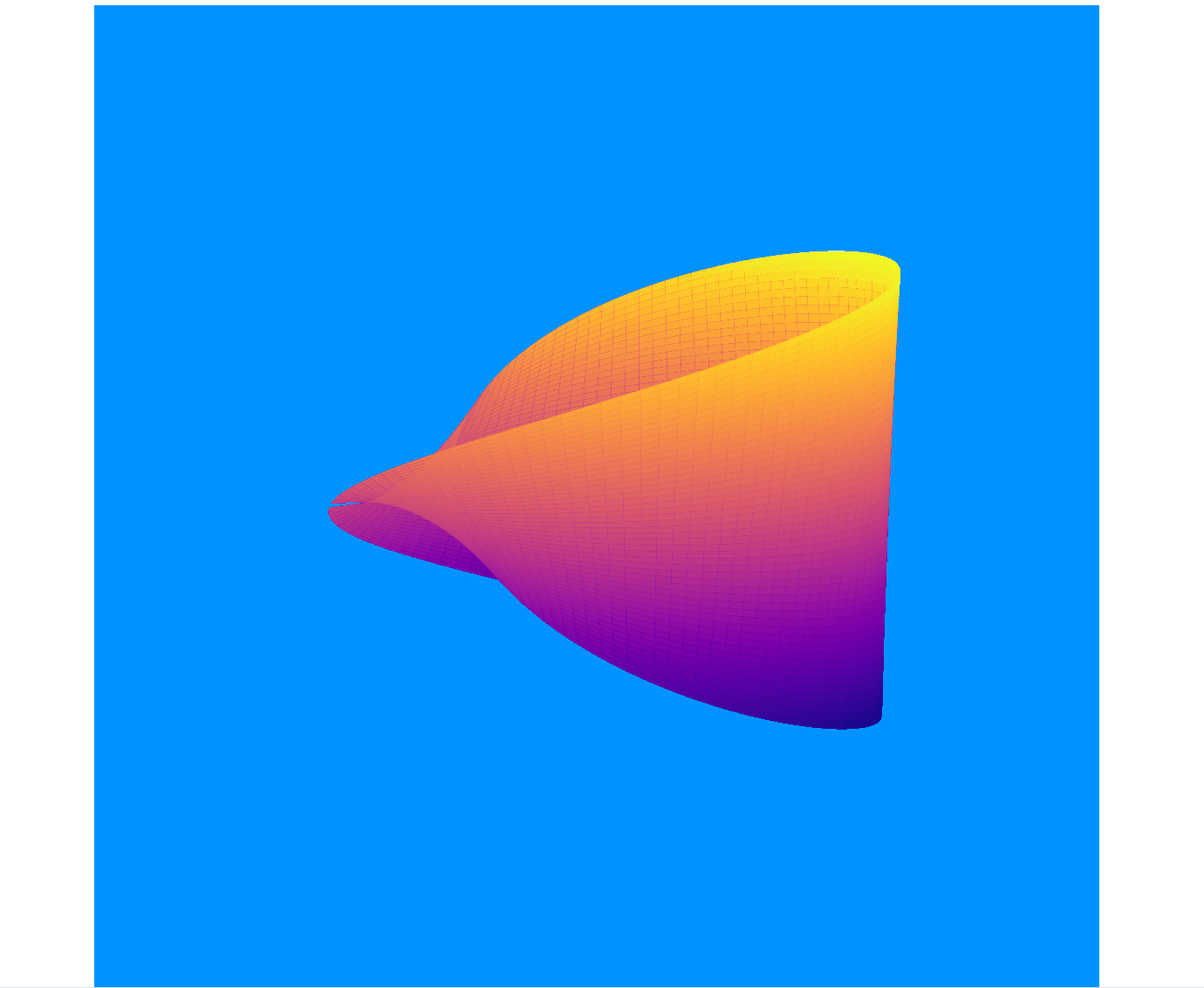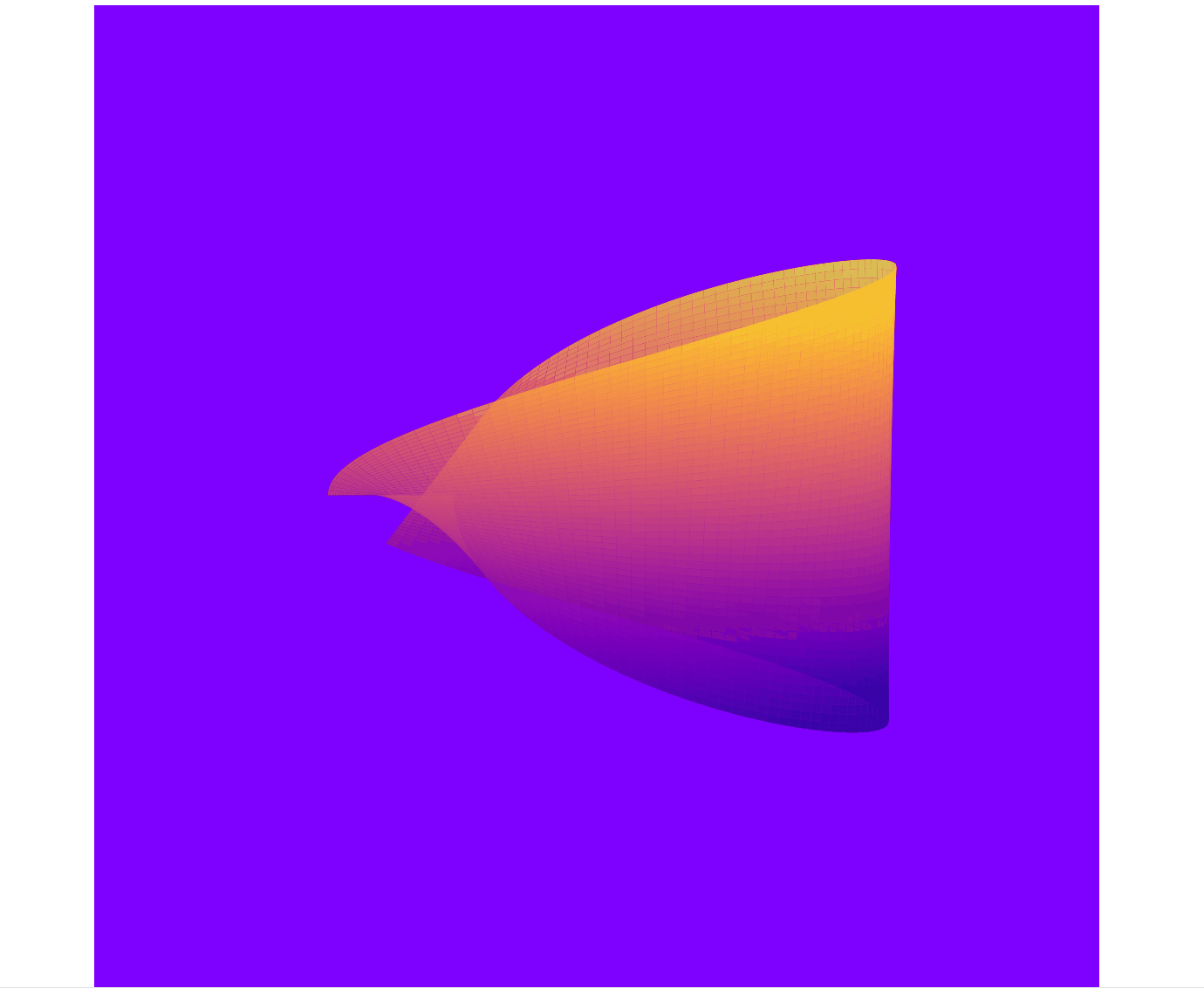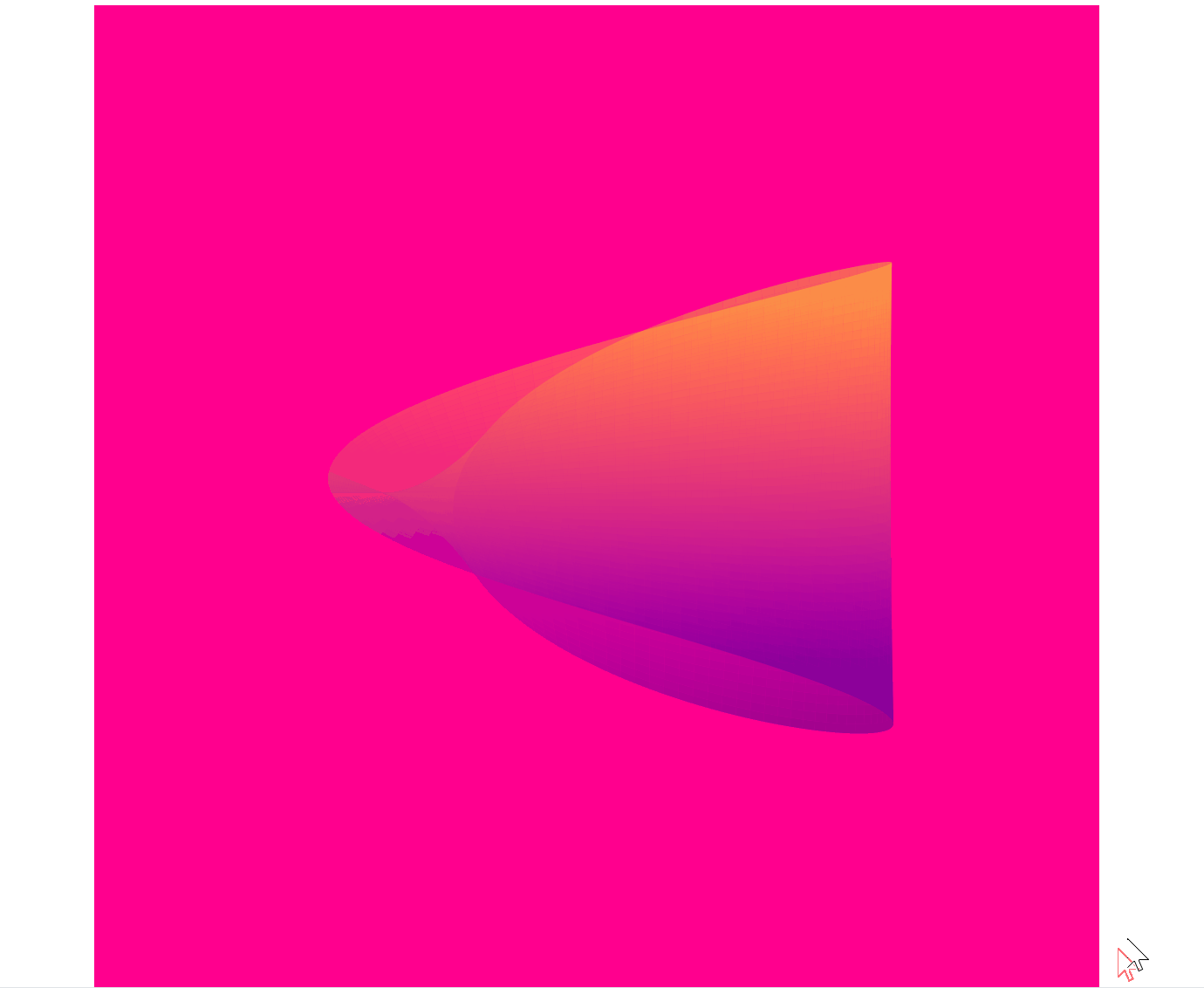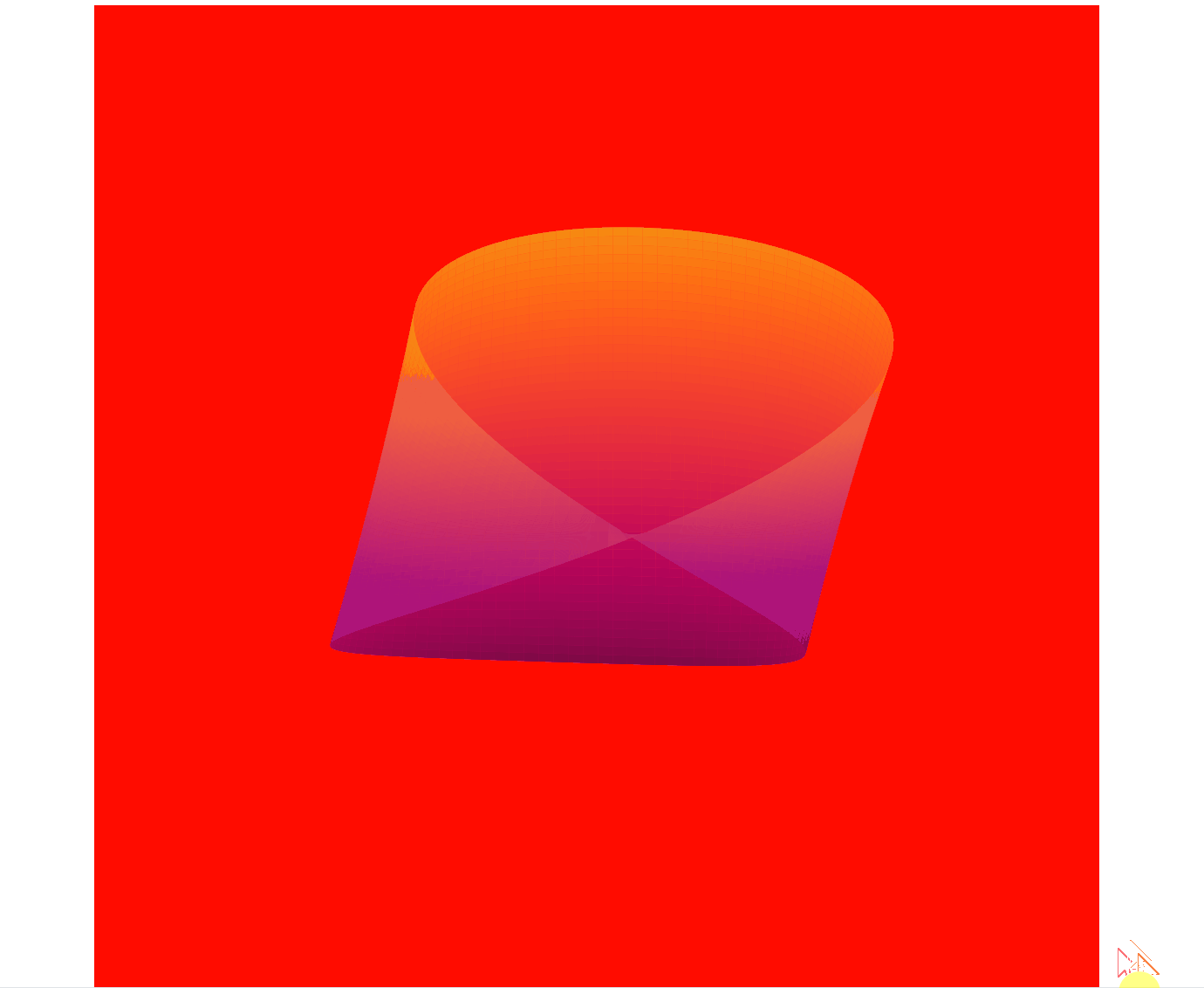
二、数学原理与参数方程

2.1 莫比乌斯带特性

莫比乌斯带不仅是数学史上的经典发现，更是理解非定向曲面的关键模型。其独特性质源于不可定向性的拓扑特征：

• ​单侧性证明实验​：用毛笔沿着表面中心线连续涂抹，最终将覆盖整个表面
• ​边界等价性​：将普通环带边界切开得到两个独立圆，而莫比乌斯带切开后仍保持单一边界
• ​手性特征​：存在左旋与右旋两种不可重合的拓扑形态

2.2 莫比乌斯带的数学原理

莫比乌斯带是一种只有一个面的几何结构，具有独特的数学性质。它的参数方程如下：

• ( x = (R + v \cdot \cos(u/2)) \cdot \cos(u) )
• ( y = (R + v \cdot \cos(u/2)) \cdot \sin(u) )
• ( z = v \cdot \sin(u/2) )

其中：

• ( u ) 是角度参数，控制莫比乌斯带的环绕。
• ( v ) 是宽度参数，控制莫比乌斯带的带宽。
• ( R ) 是主要半径，决定莫比乌斯带的整体大小。

在动画中，我们通过时间参数 ( t ) 动态调整 ( u )，使莫比乌斯带的形状随时间发生轻微变化。

2.3 参数方程解析

def mobius(u, v, t=0):
    R = 2  # 主半径
    w = 1  # 带宽
    u = u * (1 + 0.1 * np.sin(t))  # 动