机器学习中的正则化（Regularization）

参考知乎回答：https://www.zhihu.com/question/20924039 

以及博客  https://blog.youkuaiyun.com/jinping_shi/article/details/52433975

定义&用途

经常能在LOSS函数的后面看到额外加了一项，这一项就是用来正则化的，为了限制损失函数中一些参数

正则化是用来干什么的呢？--是用来防止过拟合的

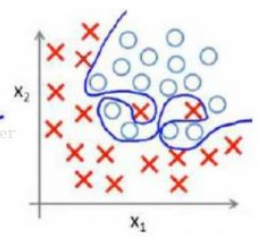
这个图表示的就是过拟合的状态，这样对训练数据的拟合度是很高的，但是换成测试数据的时候可能就准确率不够了

防止过拟合的一种方法就是减小选择的特征数量，也就是让这些特征的系数向量中一部分变为0，

n个特征前面的向量：W = {w0,w1,w2.....wn}

这就符合0范数的定义了

0范数：向量中非0元素的个数

1范数：绝对值之和   -- L1 norm L1正则化

2范数：向量的模     -- L2正则化

 

所以后面添加的项为 r(d) = “让W向量中项的个数最小化” = 

在训练中，要让loss变小，也要让W向量中项的个数变小，所以两者求和最小就好了

一般都会在正则化项之前添加一个系数

由于0范数很难求，实践中是NP完全问题，所以1范数应用的更广泛，L1范数是L0范数的最优凸近似，更容易优化求解，两者都可以实现稀疏的 —— 毕竟让参数稀疏可以去掉那些不包含什么信息的特征，并且也更有利于解释

而2范数相当于求模运算，也就是个向量的平方求和在开算术平方根，让L2范数的正则项最小，可以使得向量中各项都很小，但不会为0，只是接近0，L2范数也叫weight decay，很适合于改善过拟合。 L2范数还有助于condition number不好的情况下矩阵求逆很困难的问题（矩阵A的condition number:A的norm乘以A逆的norm）

 

 

 

解释

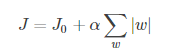带L1正则项的损失函数；也就是在后面绝对值函数的约束下，求解J的最小解

L1正则化可以产生一个稀疏权重矩阵，可以用作特征选择，一定程度上可以防止过拟合；

L2正则化也可以防止过拟合

那么为什么L1范数可以得到稀疏权重矩阵呢？ -- 因为它是L0的最优凸近似，或者说“任何的规则化算子，如果他在Wi=0的地方不可微，并且可以分解为一个“求和”的形式，那么这个规则化算子就可以实现稀疏”

 

只考虑二维（w1,w2）的情况，图片来自博客：https://blog.youkuaiyun.com/jinping_shi/article/details/52433975

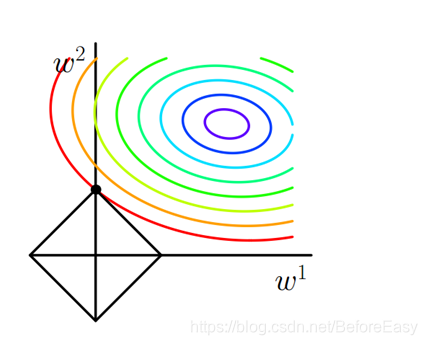图中的等值线为J0等值线，黑色直线为后面添加项的的图形，在图中，J0与添加项的图形首次相交的点即为最优解。图中可以看出，此时的交点为菱形上面那个顶点，也就是第一个w为0；

扩展到多维的情况，L1和每个坐标轴相交的地方都会有“角”出现，而目标函数与这些角相交的概率更大，而在这些角上会有很多权值为0，这就是为什么L1范式会产生稀疏的权值矩阵以及适合进行特征选择

 

类似的，L2范式的图形也可以画出来，但是图形不再是充满了棱角，而是如下所示：

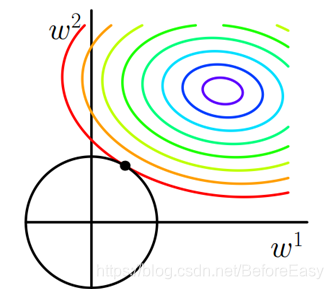
所以L2范式不会出现很多0的情况

在正则项前面的系数选择上，通常越大的系数，会让w衰减越快

 

L1 L2的区别：

 因此，一句话总结就是：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。L1在特征选择时候非常有用，而L2就只是一种规则化而已。