图卷积神经网络介绍

1. 概述

英文Graph Convolutional Networks，简称GCN。

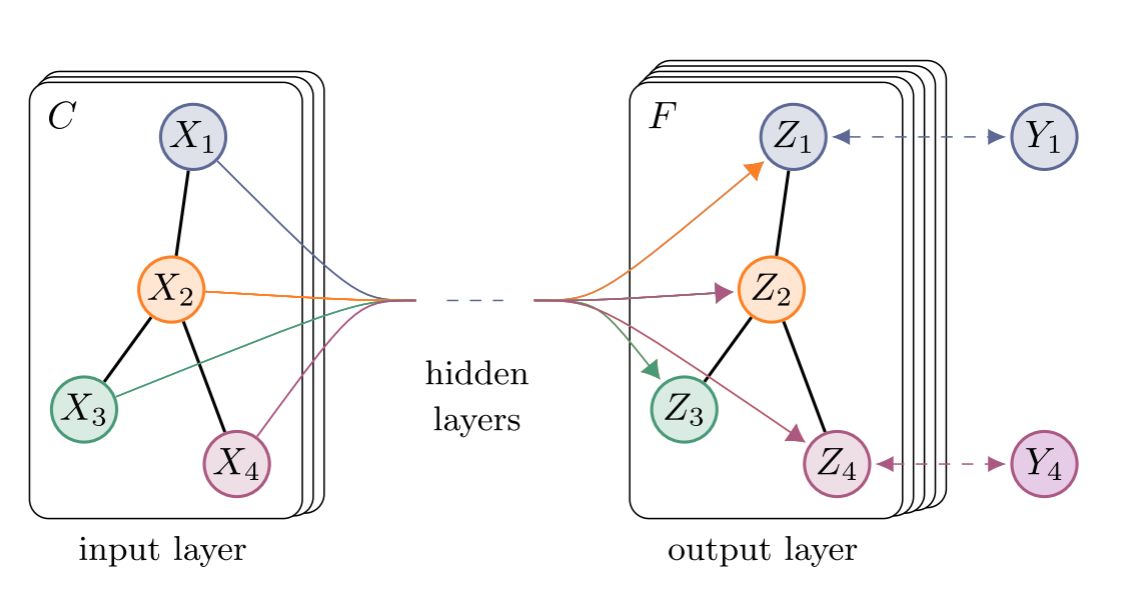
2. 矩阵介绍：

（1）邻接矩阵

英文是Adjacency Matrix，所以邻接矩阵用字母A表示。具有n个节点的图G的邻接矩阵是一个n×n的矩阵，其中矩阵的元素aij表示节点vi和节点vj之间是否存在边，如果存在，aij=1；如果不存在,aij=0。邻接矩阵也可以带权，其中元素的值表示权重。但是一般情况下不带权。

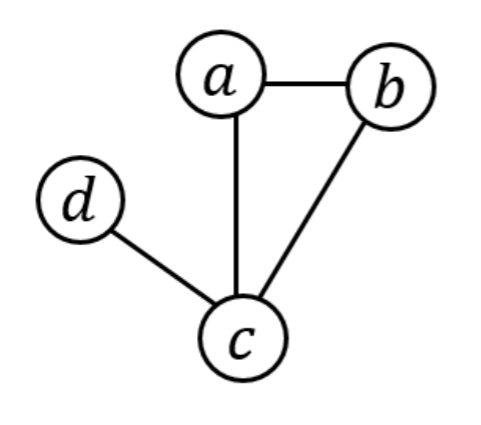
以上图为例，该无向图的邻接矩阵为：

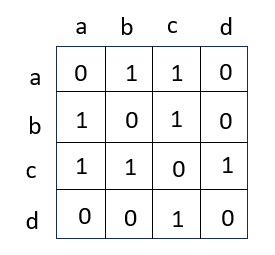
无向图的邻接矩阵为对称矩阵。

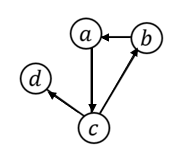
该有向图的邻接矩阵为：

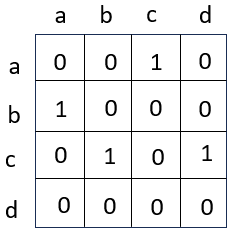
（2）度矩阵

英文是Degree Matrix，所以度矩阵用字母D表示。具有n个节点的图G的度矩阵是一个n×n的对角矩阵，其中元素dii表示节点vi的度数，dij=0。在无向图中，节点的度数指连接该节点的边的数量；在有向图中，节点的度可以是入度或者出度，分别形成入度矩阵和出度矩阵。再以下图为例：

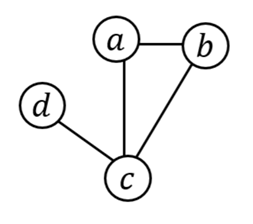
该无向图的度矩阵为：

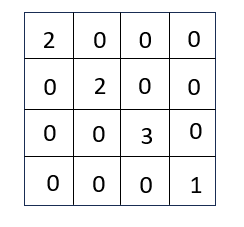
再来看有向图：

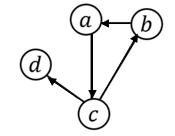
入度矩阵为：

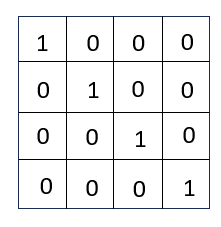
出度矩阵为：

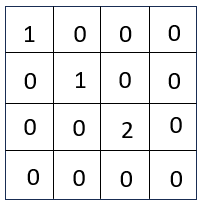
（3）带自环的邻接矩阵

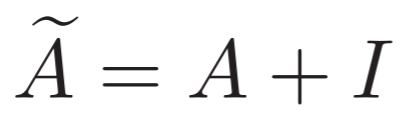
将邻接矩阵与单位矩阵相加，形成带自环的邻接矩阵：

------------->

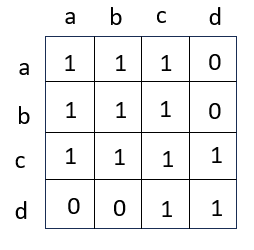
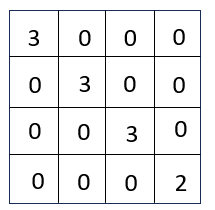
（4）带自环的度矩阵

带自环的邻接矩阵，度矩阵也随之发生变化  ：

-------------->

3. 核心公式：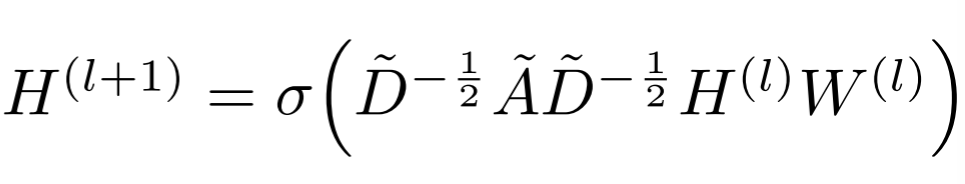

其实就是 的每个元素取倒数。 是 的每个元素取次方。

其中，W代表可学习的权重矩阵。

表示第 层输入特征的维度；

表示第 层输出特征的维度；