191112-T1~T3

T1 命令方块

题目描述

给定 $n$ 个字符串 $s_i$ ，将它们按给出的顺序排开。你每次可以交换任意两个字符串的位置。通过交换，这些字符串最终需要满足如下的性质：

对于任意的 $i<j<k$ ，必须有 $lcp(s_i,s_j)\ge lcp(s_i,s_k)$ 以及 $lcp(s_j,s_k)\ge lcp(s_i,s_k)$ 。其中 $lcp(s,t)$ 的定义为：字符串 $s$ 和 $t$ 的最长公共前缀的长度。如 $lcp("abc","abd")=2$ ，而 $lcp("abc","abcd")=3$ 。

请按顺序输出你交换了哪些字符串。保证存在一种方案，使得交换之后所有字符串满足上述性质。并且可以证明，在题目给定的范围下，这样的方案一定存在，并且你所需要的最少交换次数不会超过 $100W$ 次。

输入格式

第一行为一个正整数 $n$ ，代表字符串的个数。
接下来 $n$ 行，每行一个字符串，代表最初的 $s_i$ 。

输出格式

第一行为一个正整数 $m$，代表你的交换次数。
接下来 $m$ 行，每行两个正整数 $a,b$ ，代表你交换的两个字符串的编号。
Special Judge将会按顺序完成你给出的交换操作，并判定最后得到的字符串序列是否合法。如果你输出的 $m$ 大于 $100W$ ，或者输出格式不正确，将被认为是答案错误。如果你的答案合法并且是正确的，你将会得到对应测试点的得分，反之不得分。

数据范围

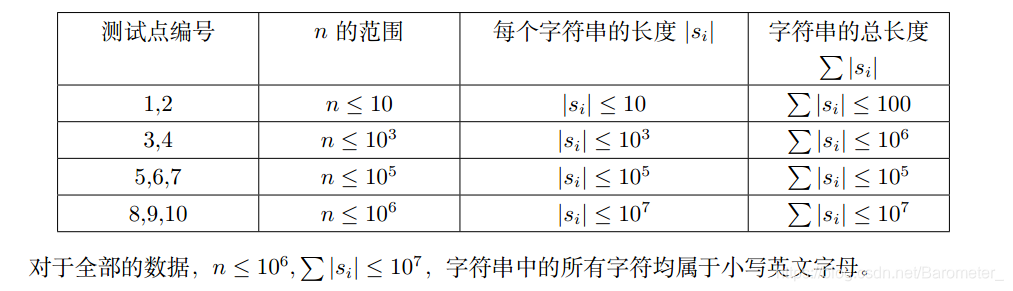
解析

$Part1$

我们可以把字符串放入一个字典树中，任意一个搜索次序都是合法的。因为字典序就是搜索次序的一种，于是我们方便起见，将 $string$ 进行 $sort$ 排序。

$Part2$

题目还要让我们输出排序的过程，可以字符串结构体再存编号，最后相当于只是编号换了。现在我们可以从左往右扫描一遍，当我们找到任何一个不在应该在的位置上的数字 $x$ ，将 $x$ 与它本应该在的位置上的数字交换。这样，在 $n$ 步之内，所有数字都可以归位。

代码

#include<bits/stdc++.h>
using namespace std;
struct node{string s;int id;}t[1234567];
bool cmp(node xx,node yy){
	if(xx.s!=yy.s)return xx.s<yy.s;
	return xx.id<yy.id;
}
int n,ans,p[1234567],q[1234567],pos[1234567];
pair<int,int>a[1234567];
int main(){
	cin.sync_with_stdio(0);
	cin>>n;
	for(int i=1;i<=n;i++)cin>>t[i].s,t[i].id=i,q[i]=i;
	sort(t+1,t+n+1,cmp);
	for(int i=1;i<=n;i++)p[i]=t[i].id,pos[i]=i;
	for(int i=1;i<=n;i++){
		int j=pos[p[i]];
		if(j!=i){
			pos[p[i]]=i,pos[q[i]]=j;swap(q[i],q[j]);
			a[++ans].first=i,a[ans].second=j;
		}
	}
	cout<<ans<<"\n";
	for(int i=1;i<=ans;i++)
	cout<<a[i].first<<" "<<a[i].second<<"\n";
	return 0;
}

反思：缺少在字符串排序的经验，并且暴力打挂了，幸亏有零的数据，只得了 $30$ 分。

T2 骨粉

题目描述

小F今天AK了CSP内心飘飘欲仙，玩起了电竞。他这次遇到了 $n$ 名对手的强度分别为 $t_i$ 单位。他有一个强悍的法术，就是每过一个单位时间所有对手受到 $1$ 个单位的伤害。另外他还会每单位时间对指定一个人释放 $x$ 点的大招伤害，他还是认为对方太强了，于是找到了你，问你 $s$ 单位时间后，最大的 $t_i$ 最小是多少。如果全员阵亡，输出 $0$ 。

输入格式

第一行三个整数 $n,m,x$ ，代表每个对手的人数，询问的个数，大招的效用。
第二行 $n$ 个整数 $t_i$ ，代表每个人的初始强度。
接下来 $m$ 行，每行一个整数 $s_i$ ，代表一次询问。

输出格式

共 $m$ 行，每行一个整数，代表每次询问的答案。

数据范围

解析

$Part1$

由于群攻对手血量差不变，可以先把大众衰减的部分忽略掉。由公理，每次选择最大的数减肯定不会不是最优解之一。现在 $30$ 分了。

$Part2$

由于值域非常大，一步一步爬肯定不行，于是就有二分答案。设二分出最小的最大的强度 $t_i$ 值为 $v$ 。则每一人需要大招数量为：

$$\max (\lceil \frac{(t_i-v)}{x}\rceil ,0)$$

可以得 $60$ 分。

$Part3$

为了让一次询问的复杂度小于 $O(n)$ ，我们还要继续分析。有上式可以推导（中括号是如果满足取1否则取0）出：

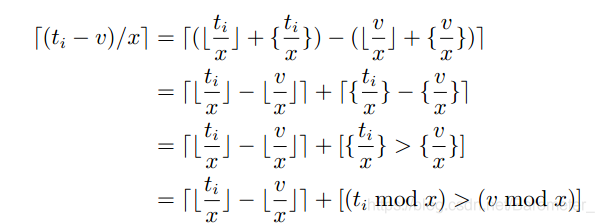
在二分的时候我们要找到所有满足 $t_i>v$ 的人，并且还要知道这些人中多少满足 $(t_i\mathrm{m}\mathrm{o}\mathrm{d}x)>(v_i\mathrm{m}\mathrm{o}\mathrm{d}x)$ 。可以在线回答，能用主席树来维护最后那个中括号，模数作为下标，记录出现次数。（记得梨伞花和开log2N倍数组）
单点插入：以模数为下标，增加出现次数。
区间询问：第K大数问题，用后缀和。
期望得分： $100$ 分，时间复杂度 $O(n{\log }_{2}n+m{\log }_2^{2}n)$ 。

#include<cstdio>
#include<cstring>
#include<algorithm>
#define int long long
using namespace std;
struct node{int ls,rs,x;};
namespace fhl{//封装
	int cnt;node tre[7777777];
	void Insert(int &a,int l,int r,int p,int x){//插入点
		tre[++cnt]=tre[a];a=cnt;
		if(l==r){tre[a].x+=x;return;}
		int mid=(l+r)>>1;
		if(p<=mid)Insert(tre[a].ls,l,mid,p,x);
		else Insert(tre[a].rs,mid+1,r,p,x);
		tre[a].x=tre[tre[a].ls].x+tre[tre[a].rs].x;
	}
	int Query(int a,int l,int r,int x,int y){//问第K大数
		if(!a)return 0;
		if(x<=l&&r<=y)return tre[a].x;
		if(x>r||y<l)return 0;
		int mid=(l+r)>>1;
		return Query(tre[a].ls,l,mid,x,y)+Query(tre[a].rs,mid+1,r,x,y);
	}
}
int n,m,x,val[123456],id[123456],sum[123456],rt[123456];
void Init(){
	for(int i=1;i<=n;i++)id[i]=val[i]/x;//要打几次
	for(int i=n;i>=1;i--){
		sum[i]=sum[i+1]+id[i];//后缀和
		rt[i]=rt[i+1];//多个根
		fhl::Insert(rt[i],0,x,val[i]%x,1);//动态开点
	}
}
int check(int tar){//验证二分答案
	int p=lower_bound(val+1,val+n+1,tar)-val;//梨伞花
	int ret=sum[p]-(tar/x)*(n-p+1);//就是最大的公式
	ret+=fhl::Query(rt[p],0,x,tar%x+1,x);//第K大数问题
	return ret;
}
signed main(){
	scanf("%lld%lld%lld",&n,&m,&x);
	for(int i=1;i<=n;i++)scanf("%lld",&val[i]);
	sort(val+1,val+n+1);Init();//预处理，并且把最大弄出来
	for(int i=1;i<=m;i++){
		int tt;scanf("%lld",&tt);
		int l=0,r=val[n],ans=0,mid;
		while(l<r){
			mid=(l+r)>>1;
			if(check(mid)>tt)l=ans=mid+1;//不够，少了
			else r=ans=mid;//多了
		}
		ans=max(ans-tt,0ll);//tt是过去的时间，减去即可
		printf("%lld\n",ans);
	}
	return 0;
}

我考场暴力算法有问题，当有元素相同的时候输出是 $0$ 。

T3 字符串问题（源于CF520E）

题目描述

给定一个 $n$ 位的十进制数，可以再数字之间加 $k$ 个 $+$ 号（允许前导零），得到一个算式，求每种方案的这个算式的答案总和$\mathrm{m}\mathrm{o}\mathrm{d}998244353$。

输入格式

第一行，两个正整数 $n,k$ ，表示字符串长度和加号的数量
第二行是长度为 $n$ 的字符串，由数字字符 $0\sim 9$ 组成。

输出格式

只有一行，只有一个数，表示你的答案。

解析

Lv. 1

直接状态压缩，时间复杂度 $O(?\ast 2^n)$ ，期望得分 $0$ 。

Lv. 2

暴力枚举加号的位置，期望得分 $10$ 。

Lv. 3

$f[i][j]$ 表示用了 $i$ 个加号，最后一个加号位置是 $j$ 的所有方案的答案和，暴力转移。 $O(n^3)$ ，期望得分 $30$ 。

Lv. 4

每一个数字多次作为不同的数位对答案进行贡献。枚举第 $i$ 个数字对答案的贡献是 $10^j$ ，系数是 $C_n^m$ 最后乘 $i$ 。注意如果第 $i$ 个数字后面都没有加号要单独处理只枚举非 $0$ 数字可以通过特殊性质的数据。时间复杂度 $O(n^2)$ ，期望得分 $60$ ~ $80$ 。

Lv. 5

先预处理一堆阶乘即逆元，打好快速幂。
设 $f[j]$ 表示顺数位置 $j$ ，它可以最大贡献 $k\ast 10^{n-j-1}$ ，此时卡死或断定后面加号的位置或没有加号。如果不是最大贡献，则后面有 $+$ 号，然后又是一片自由的位置，合并到前面做组合数计算就行了。分类讨论。

1. 后面有加号：正好这个情况是可以从余下 $n-j-1$ 个数推导过来，一个加号被卡死，所以做一次只管当前的最大贡献的后缀和，各有 $C_{i-1}^{k-1}$ 种。
2. 后面无加号：第二种情况就是正向扫一遍，意味着这个位置贡献最大及以后无加号，各有 $C_{i-1}^k$ 种。并上前一种就结束了。

期望得分：$100$ 分，时间复杂度 $O(n)$ 。

#include<cstdio>
#define int long long
#define mod 998244353ll
using namespace std;
int n,k,ans;
char s[555555];bool bo[555555];
int jc[555555],inv[555555];
int turtle(int b,int p,int k){
	int ss=1;
	while(p){
		if(p&1)ss=ss*b%k;
		b=b*b%k;p>>=1;
	}
	return ss;
}
inline void iniit(){
	jc[0]=1;
	for(int i=1;i<=500000;i++)jc[i]=jc[i-1]*i%mod;
	inv[500000]=turtle(jc[500000],mod-2,mod);
	for(int i=499999;i>=0;i--)inv[i]=inv[i+1]*(i+1)%mod;
}
int C(int nn,int mm){
	if(mm>=0&&mm<=nn)return jc[nn]*inv[mm]%mod*inv[nn-mm]%mod;
	return 0;
}
int f[555555];
signed main(){
    scanf("%d%d",&n,&k);
    scanf("%s",s+1);
    iniit();
    for(int i=n-1;i>=1;i--)f[i]=(f[i+1]+turtle(10,n-i-1,mod)*C(i-1,k-1)%mod)%mod;
    for(int i=1ll;i<=n;i++)f[i]=(f[i]+turtle(10,n-i,mod)*C(i-1,k)%mod)%mod;
    for(int i=1ll;i<=n;i++)ans=(ans+f[i]*(s[i]-48))%mod;
    printf("%lld",ans);
	return 0;
}

我想出算法四已经没有时间了，于是只能听取蛙声一片。

加油，注意休息和放松心态