C语言数据结构-层次遍历二叉树（非递归链队列实现遍历）

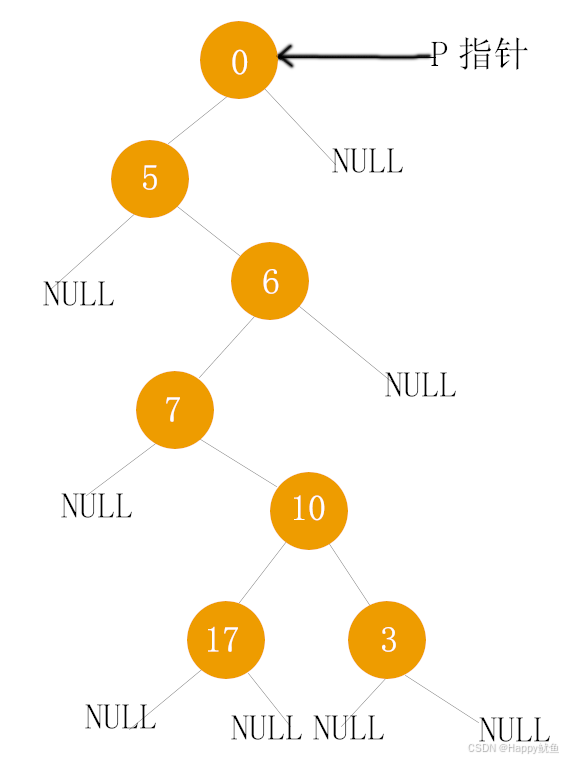
        层次遍历采用了之前已经实现的链队列作为基础，同时链队列由之前存储整数，调整为存储一级指针，代码整体逻辑基本没有变动，目的为了能够实现存储二叉树中各个结点的位置用于层次遍历。层次遍历的代码有些许难理解，可以手动画图根据顺着代码一行行对着看不算难，本案例中二叉树创建的图如下。

//基本头文件，包含printf这些最基本的函数
#include<stdio.h>
//引入malloc函数用于动态开辟二叉树结点
#include<stdlib.h>
//宏定义OK、False用于解决C语言中没有OK、False这些关键字，也可以引入其他关键字头文件，宏定义替换只是一种简单的表示方法也可以单纯的用0,1在函数中表示
#define OK 1
#define False 0
//重命名 int为Status和Element方便后面使用
typedef int Status;
typedef int Element;
#define Stack_init_size 10  // 栈的初始分配大小
#define Stackincrement 10   // 栈空间增量
#define OVERFLOW 3

//定义二叉树结点，typedef是把struct BiTree重命名为BiTree，方便后续声明二叉树结点减少代码量
typedef struct BiTree {
	Element infos;
	struct BiTree* lchild;
	struct BiTree* rchild;
} BiTree;

// 定义队列结点
typedef struct QNode {
	BiTree** data;
	struct QNode* next;
} QNode, * QueuePtr;

// 定义链式队列
typedef struct {
	QueuePtr front;
	QueuePtr rear;
} LinkQueue;

//初始化队列
Status InitQueue(LinkQueue& Q) {
	Q.front = Q.rear = (QueuePtr)malloc(sizeof(QNode));
	if (!Q.front)exit(OVERFLOW);
	Q.front->next = NULL;
	return OK;
}

//把地址存入队列
Status EnQueue(LinkQueue& Q, BiTree* e) {
	QueuePtr p = (QueuePtr)malloc(sizeof(QNode));
	if (!p) exit(OVERFLOW);
	// 分配一个 BiTree* 类型的指针空间，并将 e 的地址存储进去
	p->data = (BiTree**)malloc(sizeof(BiTree*));
	if (!p->data) {
		free(p);  // 内存分配失败处理
		exit(OVERFLOW);
	}
	*(p->data) = e;  // 将 e 的地址赋给 p->data
	p->next = NULL;
	Q.rear->next = p;
	Q.rear = p;
	return OK;
}

//删除队列第一个元素
Status DeQueue(LinkQueue& Q) {
	if (Q.front == Q.rear)exit(OVERFLOW);
	QNode* p = Q.front->next;
	if (p == Q.rear) {
		Q.rear = Q.front;
	}
	else {
		Q.front->next = p->next;
	}
	return OK;
}

//判断队列是否为空
Status QueueEmpty(LinkQueue& Q) {
	if (Q.front != Q.rear) {
		return False;
	}
	return OK;
}

//获取队列长度
int QueueLength(LinkQueue& Q) {
	if (Q.front == Q.rear)return 0;
	QNode* p = Q.front->next;
	int length = 0;
	while (p) {
		length++;
		p = p->next;
	}
	free(p);
	return length;
}

//初始化二叉树，根节点元素设置为0
Status InitBiTree(BiTree& T) {
	T.infos = 0;
	T.lchild = NULL;
	T.rchild = NULL;
	return OK;
}
//InsertChild函数 添加新节点在二叉树上，插入方式可以自己修改，这个函数较简单只实现了每一层放一个结点
//T要被添加新结点的二叉树
//形参**p意思是要接受指针的地址，用于*p = NewTree;这里改变p指针的位置，如果是一个*那么在函数内p指针更新生效，但是main函数中p指针就没有更新，下一次使用本函数指针p仍然指向的是根节点导致插入覆盖的错误
//LR参数0表示插入到左子树，1表示插入到右子树，e为新结点的元素值
Status InsertChild(BiTree* T, BiTree** p, int LR, Element e) {
	if (T) {
		BiTree* NewTree = (BiTree*)malloc(sizeof(BiTree));
		if (!NewTree)return False;
		NewTree->infos = e;
		//必须设置为NULL后续数结点个数需要用NULL值判断是否是叶子/空结点
		NewTree->lchild = NULL;
		NewTree->rchild = NULL;
		if (LR == 0) {
			//**p表示找到指针p所指向的结点位置
			(**p).lchild = NewTree;
		}
		else if (LR == 1) {
			//**p表示找到指针p所指向的结点位置
			(**p).rchild = NewTree;
		}
		//*表示找到传入的指针p，并更新指针p的值
		*p = NewTree;
	}
	return OK;
}
//访问当前结点元素
void visit(Element e) {
	printf("%d->", e);
}

//获取队列第一个元素储存的二叉树结点地址
Status GetHead(LinkQueue& Q, BiTree** e) {
	if (Q.front == Q.rear)exit(OVERFLOW);
	*e = *(Q.front->next->data);
	return OK;
}

//二叉树层次遍历算法
void LevelOrderByQueue(BiTree* T) {
	if (!T) return;
	LinkQueue Q;
	InitQueue(Q);
	BiTree* p=T;
	EnQueue(Q, p);
	while (!QueueEmpty(Q)) {
		GetHead(Q, &p); // 取出队头元素
		DeQueue(Q); // 出队
		printf("%d->", p->infos); // 访问当前结点
		if (p->lchild != NULL) {
			EnQueue(Q, p->lchild); // 左子树入队
		}
		if (p->rchild != NULL) {
			EnQueue(Q, p->rchild); // 右子树入队
		}
	}
}


int main() {
	BiTree bitree;
	InitBiTree(bitree);
	BiTree* p = &bitree;
	InsertChild(&bitree, &p, 0, 5);
	InsertChild(&bitree, &p, 1, 6);
	InsertChild(&bitree, &p, 0, 7);
	InsertChild(&bitree, &p, 1, 10);
	//手动在最后一层添加两个结点,InsertChild函数暂时只能一层插入一个结点
	p->lchild = (BiTree*)malloc(sizeof(BiTree));
	p->lchild->infos = 17;
	p->lchild->lchild = NULL;
	p->lchild->rchild = NULL;
	p->rchild = (BiTree*)malloc(sizeof(BiTree));
	p->rchild->infos = 3;
	p->rchild->lchild = NULL;
	p->rchild->rchild = NULL;
	printf("二叉树非递归（链队列）层次遍历结果如下:\n");
	LevelOrderByQueue(&bitree);
	return 0;
}

运行结果如下：