第二类斯特林数是将n个不同的球放入m个无差别的盒子中,
并且要求盒子非空的方案数。
1.通项公式为:
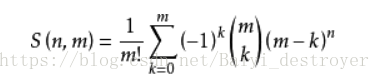
2.递推公式:![]()
证明如下:
假设要把n+1个球放入m个盒子里则分析如下:
(1)如果n个球放入了m-1个盒子,那么第n+1个球单独放入一个盒子。方案数  。
。
(2)如果n个球已经放入了m个盒子,将第n+1个球放入到任意一个盒子。方案数 m*S(n,m) 。
综合两种情况得:
代码如下:
LL stl2[5010][5010];void stl2_init()
{
for(int i=1;i<=5000;i++)
stl2[i][i]=1;
for(int i=1;i<=5000;i++)
for(int j=1;j<i;j++)
stl2[i][j]=(stl2[i-1][j-1]+j*stl2[i-1][j]%MOD)%MOD;
}
3.利用公式展开m的n次方
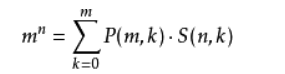
























 2675
2675

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








