Logistic回归

原创于 2023-11-21 14:51:38 发布 · 135 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#回归 #人工智能

回归问题和分类问题的最大区别：

回归的输出是一个数值，分类的输出是一组预测值。

线性回归的目标：

学习一个线性模型，能够对输入的特征X进行预测。希望学习到最好的w,b值，使预测值 $\widehat{y}$ 和 $y$ 拟合效果最好。

线性回归方程：

$y = WX+b$

数据处理：

非数值性特征（例如：颜色：{黄色，绿色，白色}）如何表示成离散的向量,形成上述公式中的特征X。

1.设置黄色为0，绿色为1，白色为2；

虽然能够使特征取值离散化，但是黄色，绿色，白色的取值和顺序挂钩是不合理的，不能说排在后面的数值就大。

解决办法：对有K个可能值的特征，表示为K为的特征向量，即：

黄色：100；绿色：010；白色：001；0和1只表示是否取到该特征，使特征的取值与顺序无关。

线性回归如何学习？

我们怎么样才能学习到w，b值？我们需要设置w,b的初始值，然后评估当前 $\widehat{y}$ 和 $y$ 的拟合效果，根据一定的策略对w,b进行更新，直到得到好的拟合结果。

如何评估 $\widehat{y}$ 和 $y$ 拟合效果？

损失函数：（最小二乘法）

$argmin\sum_{i=n}^{i=0}(\widehat{y}-y)^{2}$

更新w,b的依据是什么？

梯度更新算法。

从零开始实现：

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l
import matplotlib.pyplot as plt

#生成数据集
# true_w = torch.tensor([2, -3.4])
# true_b = 4.2
# features, labels = d2l.synthetic_data(true_w, true_b, 1000)
# 读取数据
import pandas as pd
data = pd.read_csv('temper.csv',names=['temp_2','temp_1','average','actual']) # 读取文件，指定列名
data.head()
print(data)
#归一化（由于特征数据相差不大，不进行归一化处理）
def normalize_feature(data):
	return (data - data.mean()) / data.std() # data.mean()为均值，data.std()为方差

data = normalize_feature(data)
data.head()
print(data)
#获取数据的散点图
# 获取坐标分布
#:表示所有行 0：1表示第0列；
#temp_2和temp_1对actual的影响
X1 = data.iloc[:,0:1]
X2 = data.iloc[:,1:2]
Y= data.iloc[:,-1]

fig = plt.figure()
ax = fig.gca(projection='3d')  			# 创建三维坐标
ax.scatter(X1,X2,Y)						# 散点图 				
ax.set(xlabel='temp_2',ylabel='temp_1',zlabel='actual')# 坐标轴
plt.show()
#构造数据集
# 添加 x_0=1这一列
data.insert(0,'$x_0$',1)

# 通过切片操作获取输入向量和输出向量
cols = data.shape[1] 
X = data.iloc[:,0:cols-1] 
y = data.iloc[:,cols-1:cols] 

# 将dataframe转成数组
X = X.values
y = y.values

#设置目标函数
def costFunction(X, y, theta):
	inner = np.power(X @ theta - y, 2)  # power(*,2)使向量(Xθ-y)每一项平方，返回仍为向量
	return np.sum(inner) / (2 * len(X)) # 求向量每一项之和，结果相当于(Xθ-y)自身的内积



#梯度下降的公式
def gradientDescent(X,y,theta,alpha,iters,isprint=False):
    costs = []
    
    for i in range(iters):
        theta = theta - (X.T @ (X@theta - y) ) * alpha / len(X)
        cost = costFunction(X,y,theta)
        costs.append(cost)
        
        if i % 100 == 0:
            if isprint:
                print(cost)
            
    return theta,costs
# #初始化theta的维度

candidate_alpha = [0.0003,0.003,0.03,0.0001,0.001,0.01]
iters = 2000
fig,ax = plt.subplots()
theta = np.zeros((4,1))
print(X.shape,y.shape,theta.shape)
for alpha in candidate_alpha:
	_,costs = gradientDescent(X,y,theta,alpha,iters)
	ax.plot(np.arange(iters),costs,label = alpha)
	ax.legend()

ax.set(xlabel='iters',
 	ylabel='loss',
  	title='loss vs iters')
plt.show()

实验结果分析和总结：

数据集：temper.csv

各个属性信息如下：names=['temp_2','temp_1','average','actual']

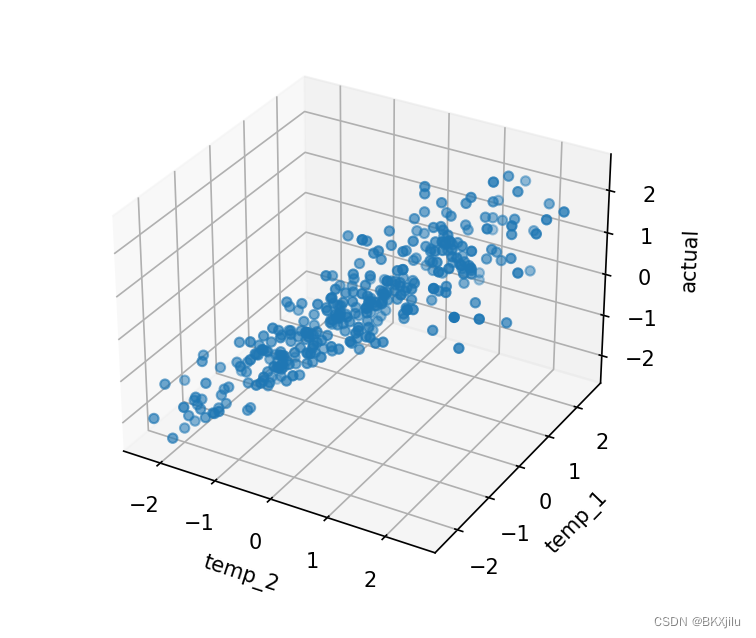
散点图：

如图可以显示：temp_2和temp_1对actual的影响

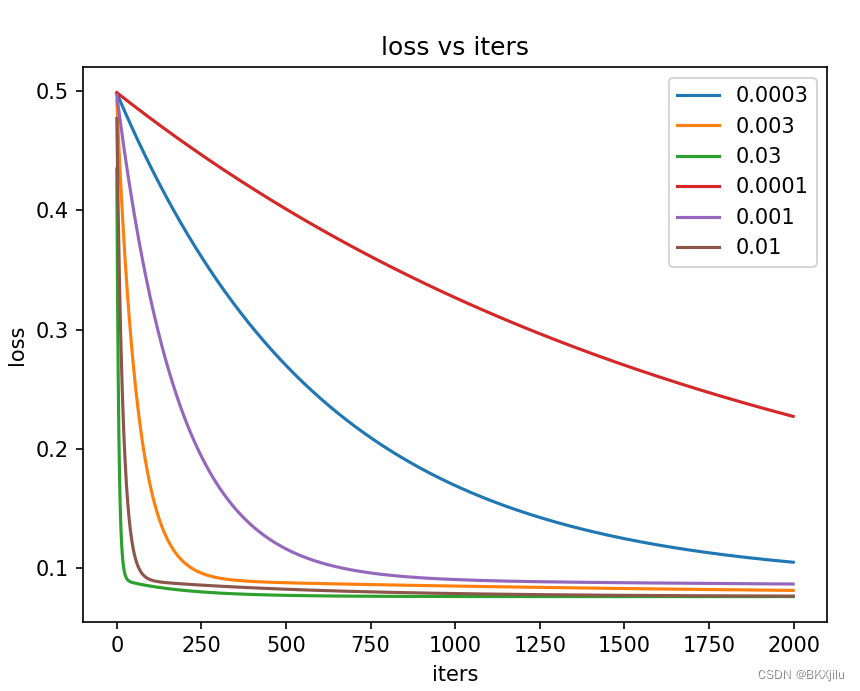
lossVS iters图：

如图可以看出：选择不同学习率对损失大小的影响。

当学习率较大时，比如为0.03，loss下降很快，收敛很快；

当学习率太小时，比如为0.0001，loss下降很慢，难以实现收敛。

学习率按照乘三除3调整，学习率的大小对模型的收敛有很大的影响，需要经过不断调试，才能得到最佳学习率。

下图中，学习率为0.003和0.01时效果最好。

d2l线性回归的实现：

（学习资料：李沐动手学习深度学习）





import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l




true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)





help(d2l.synthetic_data) 

help(d2l.reshape)
#  d2l.reshape(y, (-1, 1))



def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器。"""
    dataset = data.TensorDataset(*data_arrays)
    
    return data.DataLoader(dataset, batch_size, shuffle=is_train)




batch_size = 10
data_iter = load_array((features, labels), batch_size)






next(iter(data_iter))


# ## 3.定义模型




from torch import nn

net = nn.Sequential(nn.Linear(2, 1))




net[0].weight.data.normal_(0, 0.01)
print(net[0].weight.data)
net[0].bias.data.fill_(0)




# In[76]:


loss = nn.MSELoss(reduction='mean')
print(loss)





trainer = torch.optim.SGD(net.parameters(), lr=0.03)


# ## 7.训练



num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)
        trainer.zero_grad()
        l.backward()
        
        trainer.step()
    l = loss(net(features), labels)
    print(net[0].weight.grad)
    print(f'epoch {epoch + 1}, loss {l:f}')




w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)






# y_pre = torch.Tensor([[1, 2, 3],
#                       [2, 1, 3],
#                       [3, 1, 2]])

# y_label = torch.Tensor([[1, 0, 0],
#                         [0, 1, 0],
#                         [0, 0, 1]])
# x = torch.arange(1,10)
# criterion1 = nn.MSELoss()
# loss1 = criterion1(x, y)
# print(loss1)



torch.save(net.state_dict(), 'model1.pkl')





net.load_state_dict(torch.load('model1.pkl'))
#true_wt = torch.tensor([2, -3.4])
#true_bt = 4.2
#生成测试数据，加载模型，输入测试数据输出预测结果并计算平均损失
featurest, labelst = d2l.synthetic_data(true_w, true_b, 10)
print(labelst)
with torch.no_grad():   #测试不用更新权重
    y_hat=net(featurest)
    print(y_hat)
    train_l = loss(net(featurest), labelst)
    print(f'loss {float(train_l.mean()):f}')

实验结果：

数据集测试结果：

轮次训练的部分输出：

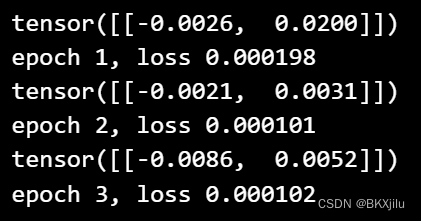
训练得到的W和b与真实值的误差:

小结：

1. 如果用`nn.MSELoss(reduction='sum')`替换`nn.MSELoss()`，为了使代码的行为相同，需要怎么更改学习速率？为什么？

默认reduction值是mean,表示差的,平方的均值，sum表示差的平方d和.由于我们计算loss时，对每个批量的样本都计算依次loss, batchsize为10，所以修改之后loss是原先的10倍。

学习率要除以batchsize。

2.查看其他损失函数和初始化方法：

# huber损失对应Pytorch的SmoothL1损失

loss = nn.SmoothL1Loss(beta=0.5)

num_epochs = 3

for epoch in range(num_epochs):

    for X, y in data_iter:

        l = loss(net(X), y)

        trainer.zero_grad()

        l.backward()

        trainer.step()  

       print(f'epoch {epoch + 1}, loss {l:f}')

epoch: 1, loss:0.00011211777746211737

epoch: 2, loss:0.00013505184324458241

epoch: 3, loss:4.4465217797551304e-05

3.如果将w和b的初始化为0，当前线性回归算法是否有效？