机器人笔记——轨迹规划

最新推荐文章于 2025-11-08 12:56:57 发布

原创最新推荐文章于 2025-11-08 12:56:57 发布 · 1k 阅读

28 ·

CC 4.0 BY-SA版权

文章标签：

#机器人 #轨迹规划 #人工智能

机器人学-学习笔记专栏收录该内容

14 篇文章

订阅专栏

前言

之前的文章讲过到了关节是持续运动的，雅可比矩阵正是描述关节运动与机器人末端运动映射关系的有力工具。然而有了如何映射的工具仅仅是分析机器人运动的开始，要知道空间两点间的运动轨迹是多样的，因此就产生了轨迹规划的概念。这里讲的轨迹规划可以理解为寻求最优路径的过程，下文对其展开介绍。

前序内容

1. 什么是机器人轨迹规划？

想要解答这个问题，我们先来看什么是轨迹。

轨迹：就是机器人手臂（末端点或操作点）的位置、速度、加速度对于时间的历程；

我们在意的其实是，机器人末端轨迹对于工件的状态或相对关系，就像下面右侧图一样，我们在意的是执行挂杯子的操作下，这两个空间点之间机械臂该怎样运动形成一个连续的轨迹，因此就引出来轨迹规划的概念。

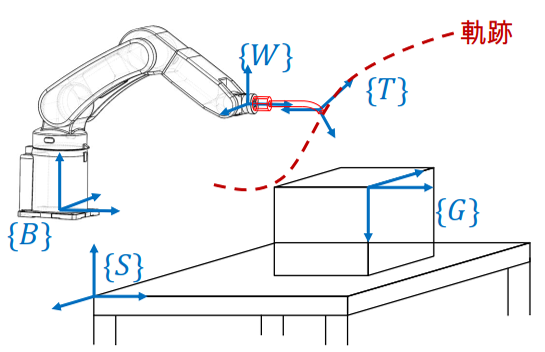
轨迹规划：根据作业任务的要求，计算出预期的运动轨迹。轨迹规划的目的主要是机器人关节空间移动中使得机器人的运行时间尽可能短。

与轨迹规划不同的还有任务规划与路径规划：①任务规划：对机器人的操作顺序、行动步骤和作业进程的规划（也就是让机器人将杯子挂到墙上这一任务中，规划机器人先抓杯子再去挂到墙上）；

②路径规划：对作业任务中位置和姿态的规划（挂杯子任务中，想让其经过哪些确定的位置，在这一位置下是怎样的姿态，比如是竖直的还是水平挂上去的）；这里路径规划的目标是使路径与障碍物的距离尽量远同时路径的长度尽量短，与速度无关。

举个例子，比如下图移动滑台上的一杯水，上面杯子无论如何移动水面都平稳，而下面的水面倾斜不平稳，这就是轨迹规划的奥妙所在了，一个好的轨迹规划算法能够使得工作任务更为顺利。所以可以看出来，轨迹规划其实就是包含时间变量的综合的规划，而不仅仅是位移的规划，也包括了对运动过程中速度、加速度的规划。

1.1 轨迹规划中的运动

其实对于不同种类的机器人，其轨迹规划的侧重点也有所不同。比如扫地机器人、VGA小车等，主要是对环境反馈或已有地图确定要按照什么样的路径来行走。对于工业机器人如焊接机械臂等，主要是对其末端行走的曲线轨迹、速度与加速度曲线进行规划。

所以可以对于机器人作业是否对路径有要求，可以将轨迹规划中的运动分为点到点运动与连续路径运动或轮廓运动，这样可以对应设计适应运动形式的轨迹规划。①点到点运动：只规定了机器人的起始点和目标点的运动；②连续路径运动或轮廓运动：不仅规定了机器人的起始点和目标点，且必须沿着特定的路径进行的运动。

1.2 轨迹规划中的空间

实际进行轨迹规划时，轨迹的描述是在关节空间或者笛卡尔空间（操作空间）中的。

①对于关节空间的轨迹规划：

规划的是每个关节的角度（或位移）随时间如何变化（速度、加速度）。
路径只关心起点和终点的关节角度，中间过程由插值（如直线、多项式）填充，不控制机械臂末端在空间中的具体路径形状。
优点：计算简单、不会遇到“奇异点”（即机械臂卡死的状态）。
缺点：无法精确控制末端执行器在空间中的运动轨迹。

②笛卡尔空间中的轨迹规划：

规划的是机器人末端（手部）在三维空间中的位置、姿态、速度和加速度随时间的变化。
要求末端沿一条特定的空间路径（比如直线或圆弧）运动。
需通过逆运动学把末端轨迹转换成各个关节的运动指令。
优点：能精确控制末端轨迹，适合需要高精度路径的任务（如焊接、装配）。
缺点：计算复杂，可能遇到奇异点，且依赖机械臂的具体结构。

2. 轨迹规划常用方法有什么？

2.1 常用的两种方法

①给出轨迹节点上的约束：在关节空间中，直接对每个关节的角度（或位移）、速度与加速度进行时间函数设计。

要首先给选定轨迹的节点上关节的位姿、速度与加速度一组显式的约束（比如初始点速度为0、加速度为0），然后从一类函数中参数化轨迹，再将约束条件代入函数进行插值。这一过程中，约束的设定与得到的轨迹函数都在关节空间中完成，最终的结果可以直接用于电机的驱动。

关节空间轨迹规划常用方法：

多项式插值法
- 三次多项式：适用于两点间给定位置和速度约束的情况（共4个条件）。
- 五次多项式：可同时满足位置、速度和加速度的边界条件（共6个条件），轨迹更平滑，广泛用于工业机器人点到点运动。
带抛物线过渡的线性插值（Linear with Parabolic Blends, LPB）
在匀速线段两端加入加速度恒定的抛物线过渡段，避免速度突变，实现连续速度。
样条函数插值
- 三次样条（Cubic Spline）：在多个路径点之间构造分段三次多项式，保证位置和速度连续（C¹连续），部分实现加速度连续。
- B样条或自然样条：提供更高阶的光滑性（如C²连续），适用于对轨迹平滑性要求高的场景。

②给出运动路径的解析式：在笛卡尔空间中，给出机器人末端的曲线路径。怎样得到这个路径呢？需要用到某种函数逼近的方法，将其转化为关节运动的约束，然后找到满足关节运动约束的参数化路径。

笛卡尔空间轨迹规划常用方法：

直线/圆弧插补（Linear/Circular Interpolation）
工业机器人中最常见的笛卡尔路径类型。通过在起点与终点之间均匀插值位置（和姿态），逐点求逆解生成关节指令。
路径参数化 + 逆运动学求解
将路径表示为参数函数 x(s) ，其中 s∈[0,1] 为路径参数，再对一系列 si 求解 qi=IK(x(si)) 。
基于雅可比的微分运动规划（Jacobian-based Differential Kinematics）
给定期望的末端速度 x˙ ，通过 q˙=J−1(q)x˙ 实时计算关节速度，适用于实时跟踪或避障。
数值迭代法求解逆运动学（如牛顿-拉夫森法、Damped Least Squares）
当解析逆解不存在或有多解时，采用数值方法逐点求解，并结合关节限位、避奇异等优化目标。
轨迹平滑与重采样
对逆解得到的关节序列进行滤波、样条拟合或时间缩放（time scaling），以满足动力学约束并提升运动平滑性。

2.2 关节空间轨迹规划步骤

由于关节驱动在关节空间内是可控的，这样能够避免机构产生奇异问题；同时由于不用考虑末端路径形状，计算简单，因此在工程实践中广泛采用关节空间的轨迹规划。下面讲解关节空间轨迹规划常用方法。

规划步骤：

① 运动学反解实现路径点在关节空间内的描述；
② 对每个关节拟合光滑函数；(轨迹规划)
③ 一段路径各关节设定相同的运动时间，确保所有关节同时到达路径点和终点（虽然同时运动同时停止，但是规划的各个关节函数之间应是相互独立的）。

那么如何获得连续光滑且独立的关节拟合函数呢？

① 首先确定关节空间内机器人在起始点、终止点的形位；

② 各形位点的速度、加速度信息（约束）；

③ 列出轨迹函数通式并求解；（这里轨迹函数一般常用的有：三次多项式插值函数、高次多项式插值函数与抛物线过渡插值函数）为什么和插值函数联系起来了呢？实际上轨迹规划就是将离散的作业点，通过插值的方式得到轨迹函数。

三次多项式插值

Eg：关节角度三次多项式插值：

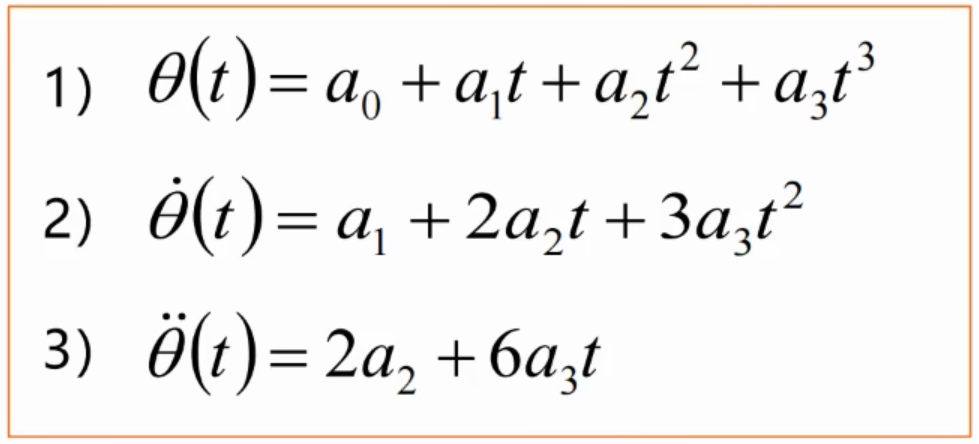
构建的是三次，四个待定系数的函数。所以需结合至少四个约束来解出这几个未知的四个变量，这样即可得到这个关节的轨迹规划函数。对第一个式子进行一次求导和二次求导，得到关于速度和加速度的2）、3）通式，再代入下面的约束条件即可求得。（f下标代表结束位置处，0下标为开始位置处）

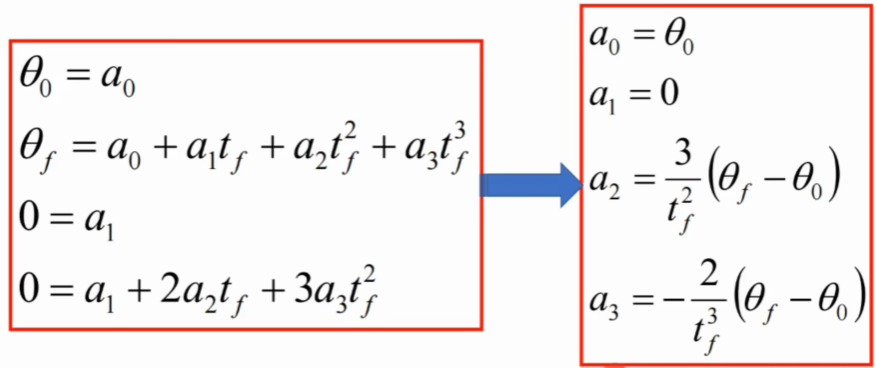
上面其实约束只给了初始点与终止点，那么如果也对中间某一点进行约束呢（也就是下面末端在A、B点速度为0，而中间点C、D的速度不为0）？

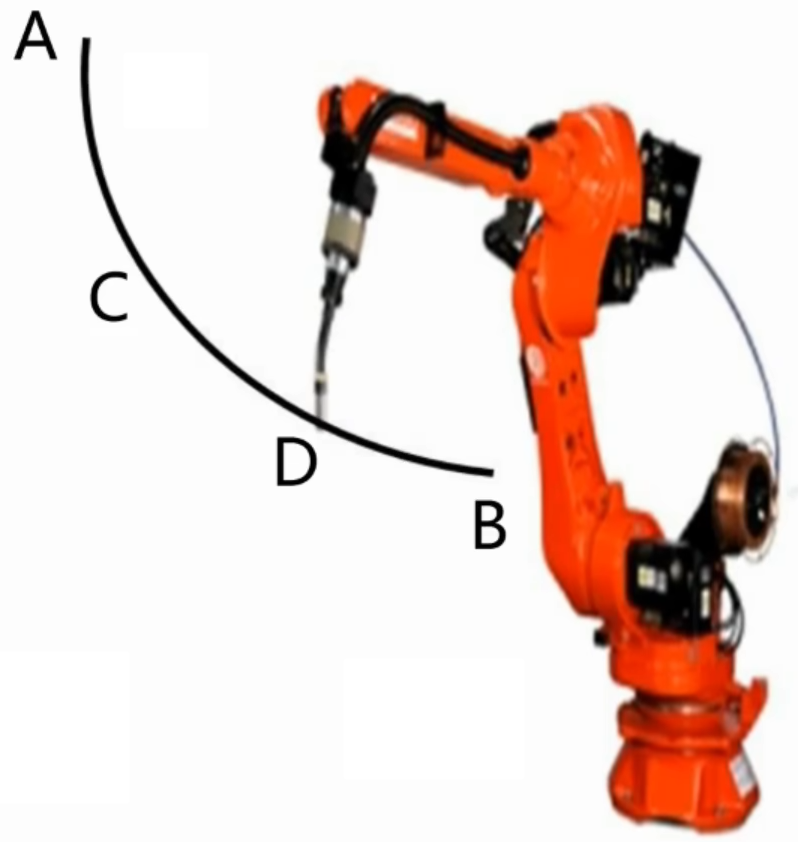
将约束条件修改为：

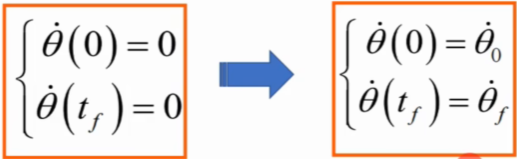
以上就可以得到轨迹规划函数了，那如何确定约束中的那个关节速度呢？

① 根据工具坐标系在直角坐标空间中的瞬时线速度和角速度来确定每个路径点的关节速度；

这种方法要求在每一个路径点进行雅可比运算，若已知末端在某路径点的期望线速度 v 和角速度 ω ，可组成末端速度向量；利用当前关节空间构型 q 计算雅可比矩阵 J(q) ；

② 在直角坐标空间或关节空间中采用某种适当的启发式方法，由控制系统自动地选择路径点的速度；

常用启发式：设中间点速度为相邻两段位移的“平均斜率”。例如，对关节角度序列 θ0,θ1,θ2,…,θn ，在第 i 点（非端点）设：
$\dot{\theta}_i = \frac{\theta_{i+1} - \theta_{i-1}}{t_{i+1} - t_{i-1}}$

上式称为中心差分法，常用于三次样条的“自然”或“非节点”边界条件。
也可设为零（如停顿点），或按任务需求手动指定。