前言
前面几篇文章讲到了什么是正逆运动学,有何用处,以六自由度机械臂为例说明了应该如何计算。本文就以典型的双平行四边形机构的码垛机械臂为例,以更为直观的几何法去求解机械臂的运动学,包括如何建系、数学建模以及Matlab解算等。
前序内容
- 机构自由度的计算
- 齐次变换与齐次变换矩阵的计算
- 机器人正运动学——学习笔记
- 机器人正运动学实例——PUMA560机械臂(附Matlab机器人工具箱建模代码)
- 机器人逆运动学——以六自由度机器人为例(详解、易懂,附全部Matlab代码)
一、机械臂结构与运动分析
本文案例针对的是三自由度码垛机械臂,为双平行四边形机构,三维结构如下图所示。
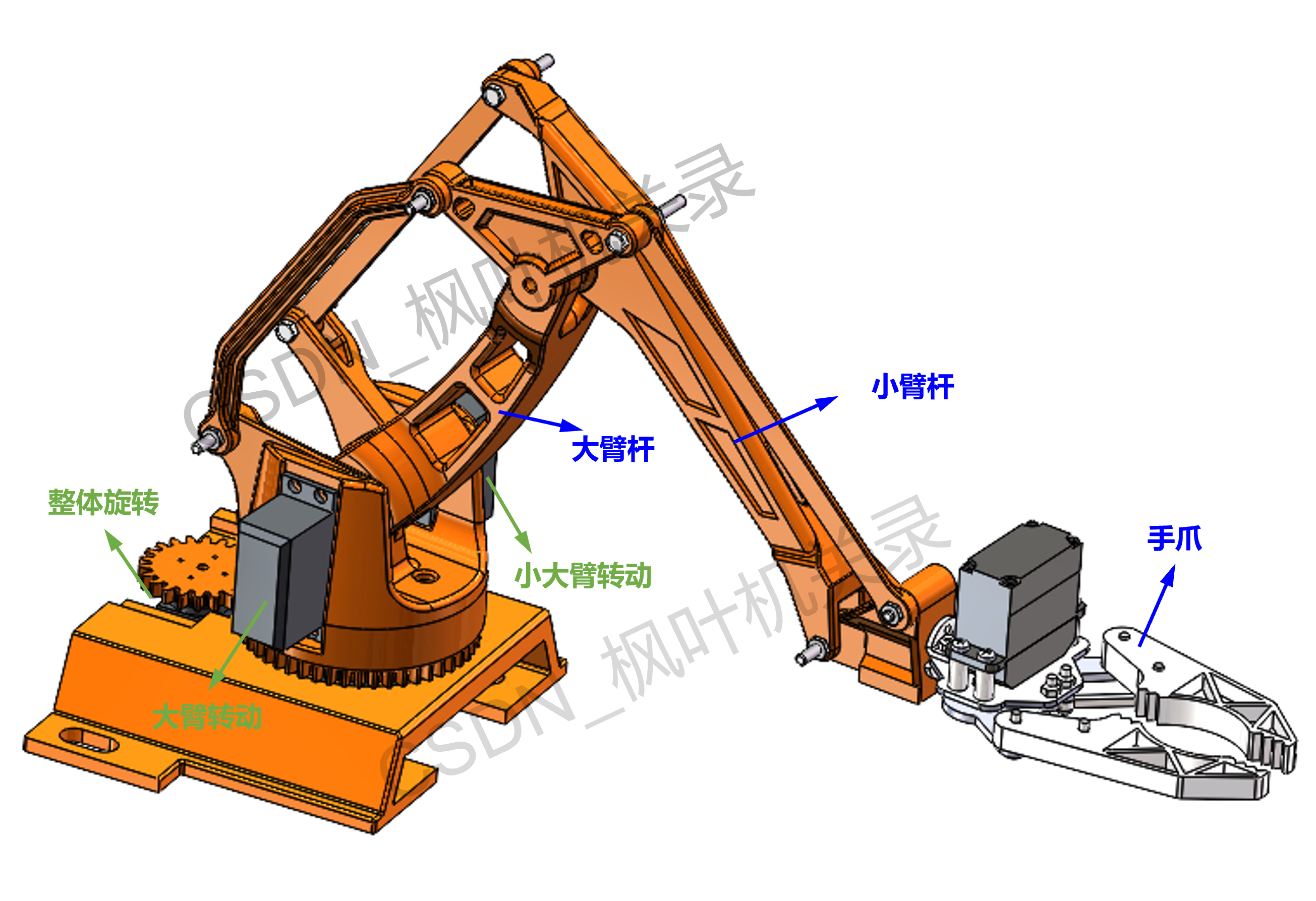
三自由度是指下面齿轮传动的一个转动自由度,以及大臂小臂的两个自由度,图中都是用舵机驱动的。末端是一个单自由度的夹爪,也是依靠舵机驱动的。
*后文主要针对机械臂运动分析,为方便观察,后面内容隐藏夹爪结构(分析末端夹爪位姿,可以把其看作是末端三角连接件的固连构件,这里不展开讨论)。
1. 机构运动分析
下图就是双平行四边形机构机械臂的分析图:
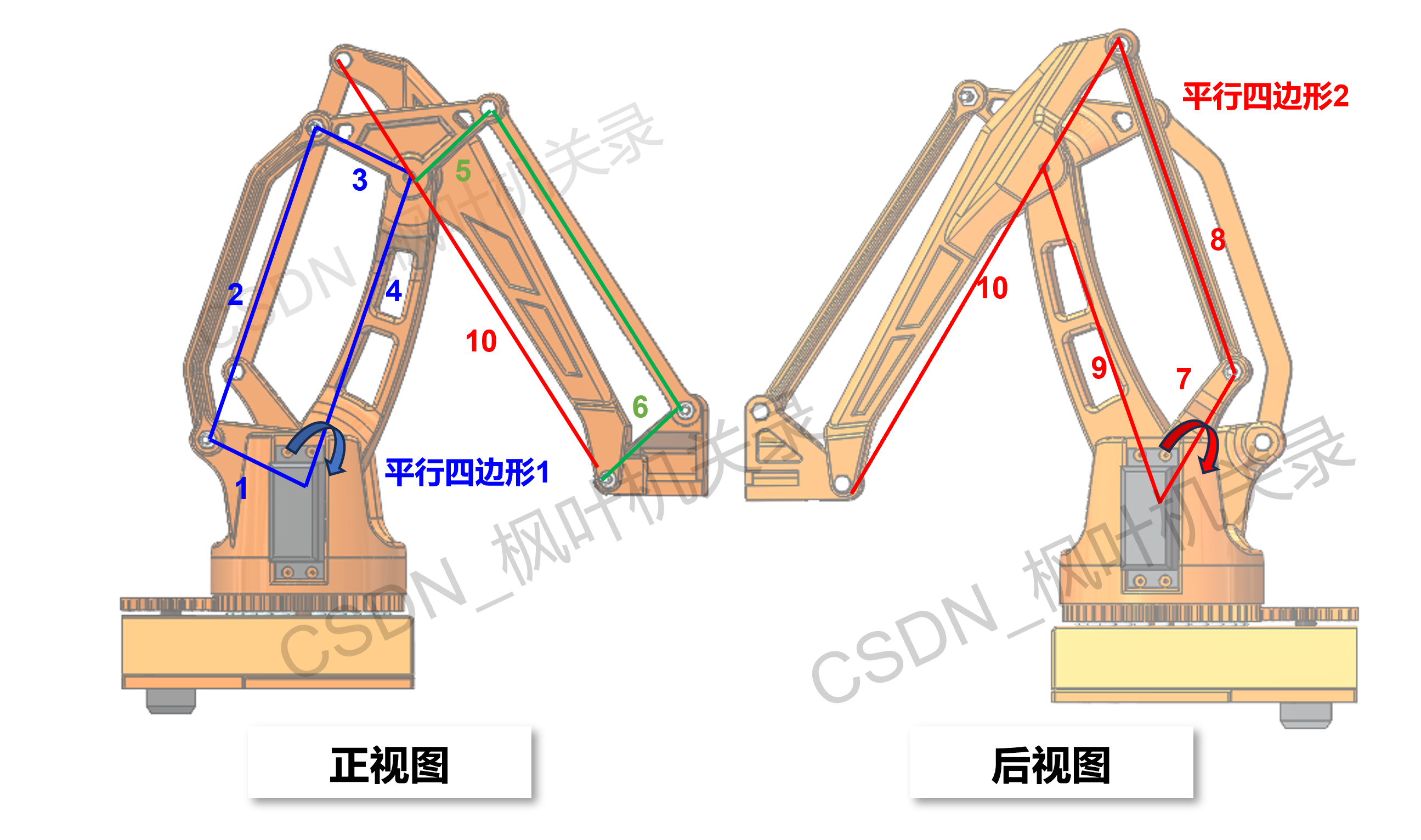
可以看到上图两个视图中的蓝色与红色平行四边形结构,这就是所谓的双平行四边形结构机械臂。其实就是利用了平行四边形两对边,时刻能保持平行的性质。两者的作用就是共同使得图中末端的三角连接件时刻保持水平,也就是让固连其上的手爪保持水平。
1)正视图
实际上平行四边形1结构,主要是为了引导末端的夹爪保持水平。当大臂杆4转动时,会带动平行四边形1中与大臂对应的连杆2转动。需要注意的是这个平行四边形中杆1是固定不动的,所以无论大臂如何运动,上面三角形连接块的边3也不会转动(只会跟着平动)。
机构的精巧也在于这个三角连接块与后面的绿色平行四边形,杆3不转动也就意味着杆5不转动(同一构件)。在绿色平行四边形中的杆6与杆5平行,所以末端的杆6对应的执行器也不会转动。但是这一前提是小臂杆10与绿边共同构成了平行四边形。
2)所以再来看后视图:
小臂杆10与杆7~8组成了另一个平行四边形2,在这一结构中杆7是输入运动的构件,所以小臂会一直平行于杆7作同样的转动。所以与前面讲到的绿色平行四边形,共同就使得末端一直保持水平。
2. 动图展示
啰嗦了半天是不是有些没看明白?下面是大臂小臂的运动动图,结合上面讲解就能更好理解了:
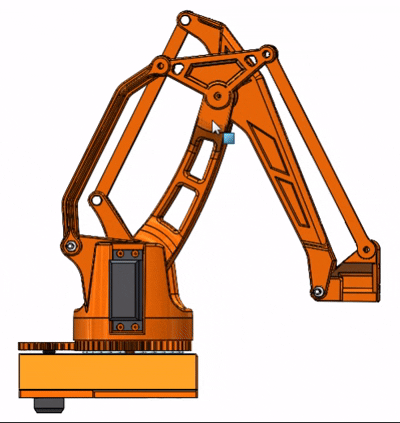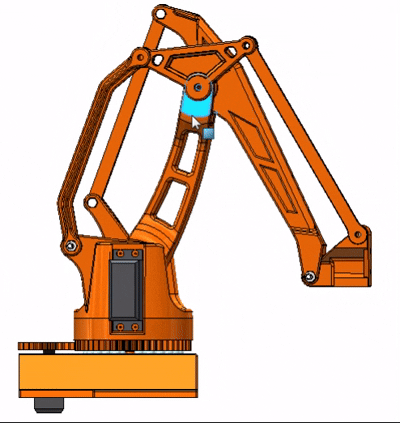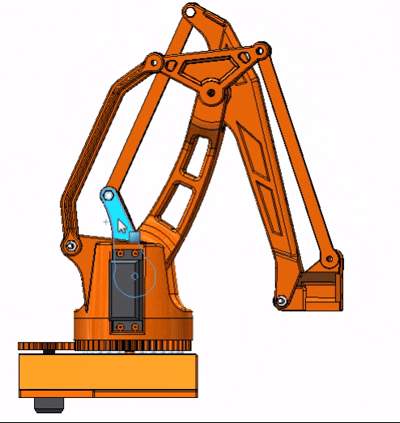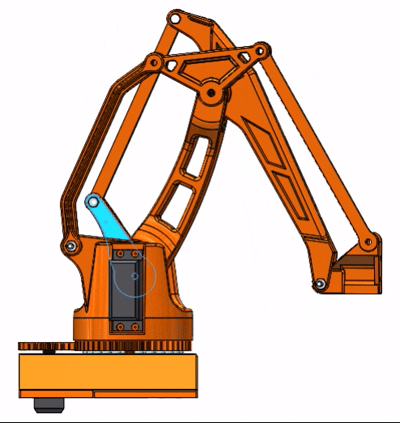
图中输入运动的就是实际舵机控制的主动杆,你可以发现无论大臂或是小臂的运动,其末端的结构都会一直保持水平,这其实就是双平行四边形机构的精巧之处了。
二、运动学具体分析
对于具体运动学分析我们可以沿用常规方法,建系、D-H参数建立、正运动学方程推导、逆运动学求解。但是从几何角度我认为其实可以将这一结构进行简化,简化至只有一个平行四边形结构,这样一来分析过程也简单很多。
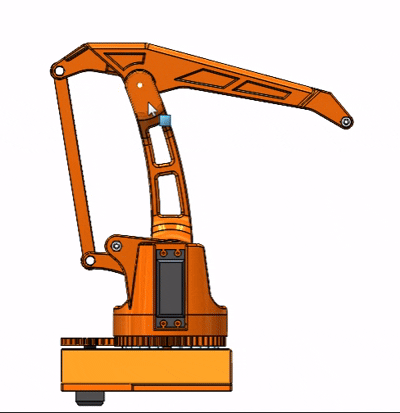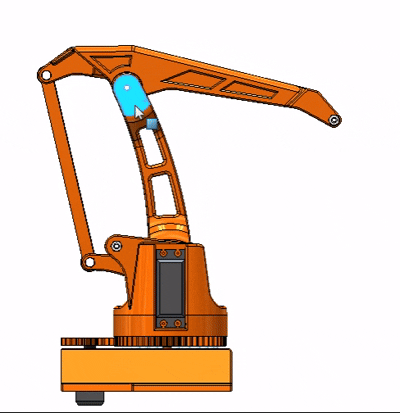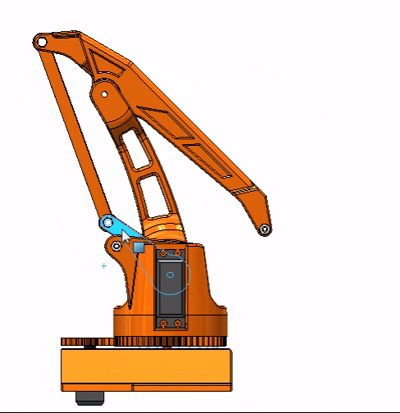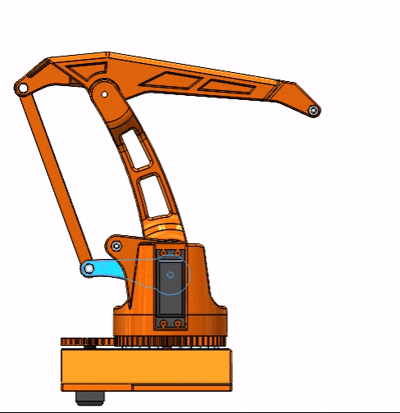
从上面看出其实与双平行四边形结构不同,我去掉了一个平行四边形,这与实际运动不同的只有末端执行器不再保持水平了,但输入与输出的运动并无变化。所以我分析这一结构,明确小臂末端点的运动,不就可以知道连接在小臂的执行器位置了吗?
1. 几何方法运动学正解
首先先看我对这一结构进行的建系与参数设置如图:
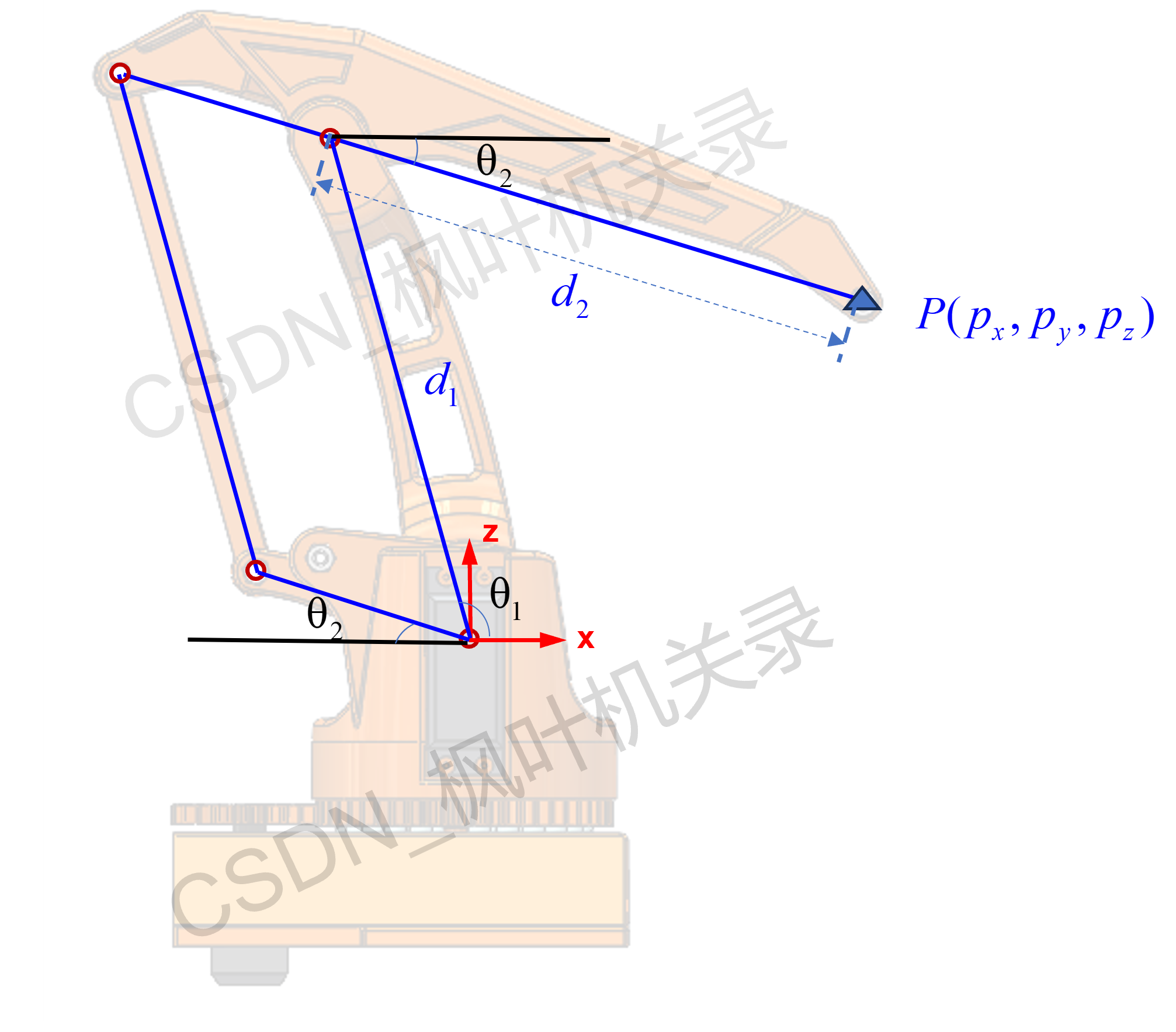
空间上的夹角定义为:大臂与水平线的夹角为,小臂与水平线的夹角为
,大臂长度为
,小臂长度为
。
① 通过几何法,先不考虑底座的转角,先考虑机械臂在这一xz平面的位姿。这样可以写出末端点P相对于基座标系得表达式:
![]()
② 然后再看底座转角与位姿的关系,如下图所示并建立如下的关系式:
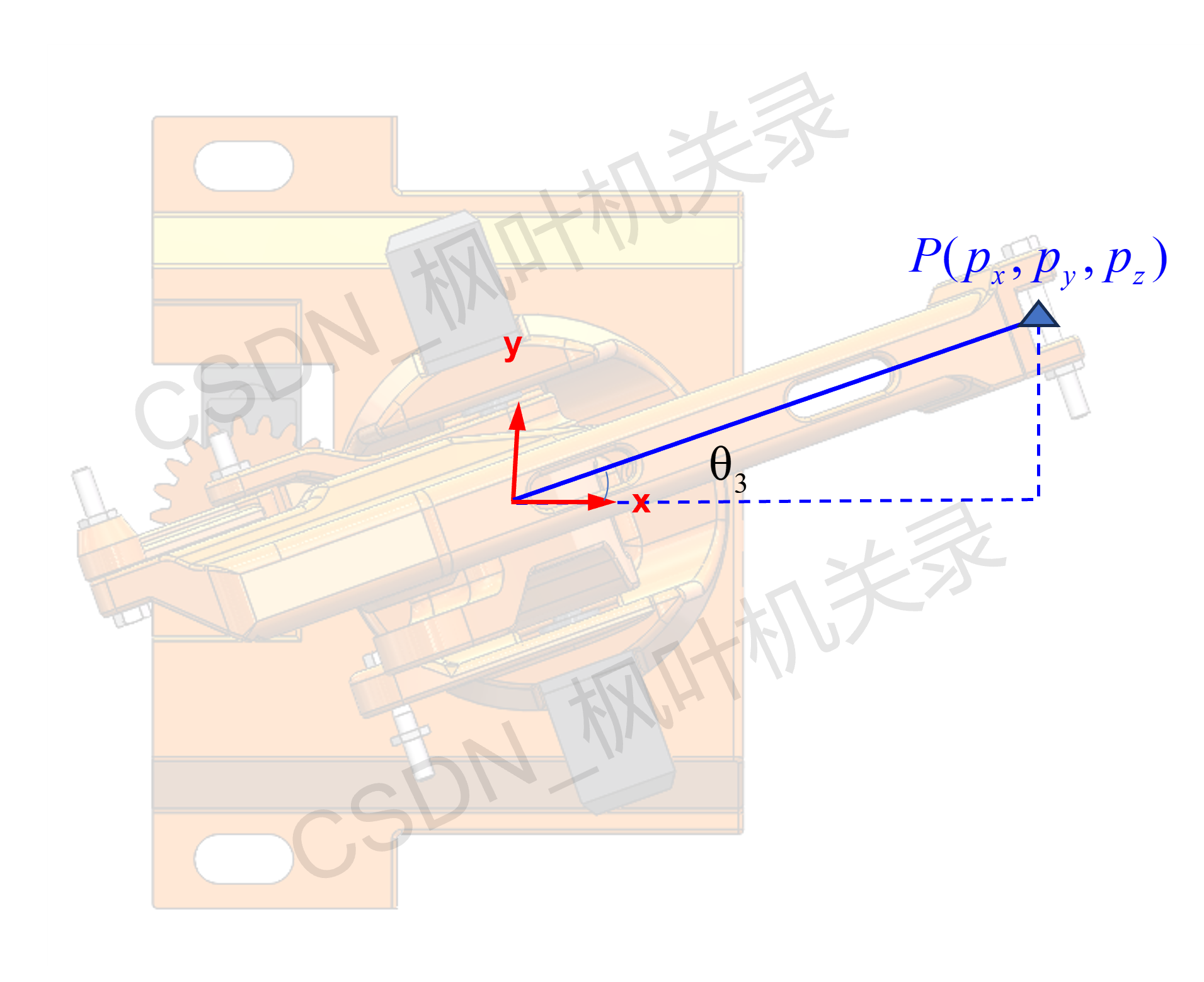
与①中方程组结合就可以得到末端位姿在基坐标系的表达了:
2. 运动学逆解
之前文章也有讲到,运动学逆解本质就是已知末端位姿的数据,反解出各个关节转角或移动距离的多少。上面我们已经获得了运动学关系,可以说知道了运动学正解,逆解就是对上面的方程组进行拆分了,以下就是逆解的计算过程。
①求解
为了简化计算,先进行xz平面的反解(先看作平面机器人),上式移项可得:
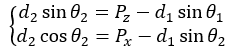
之后对方程组中两式平方求和:
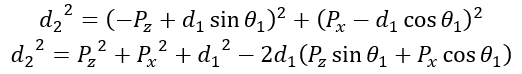
这时上式中
可以变形为:
这时引入中间变量
,并使得
,所以上式又可以变为:
因此可以对上式变形为(sin可能有两个对应的角度,都能等于等号左边):
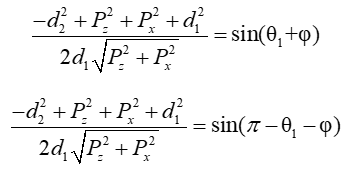
其中:
解上式就可以得到两种可能解:
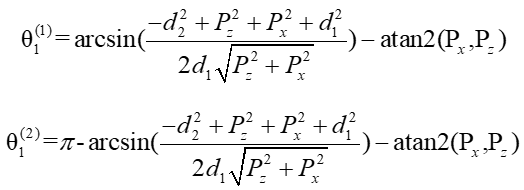
②求解
同理可以移项得到:
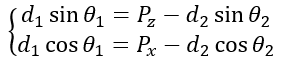
然后进行平方求和、移项变换可得到:
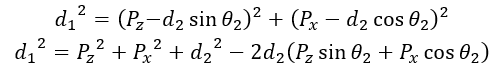
和上面求解过程一致,对上式变形得:
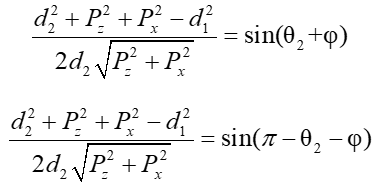
同样,解上式可以得到两组解:
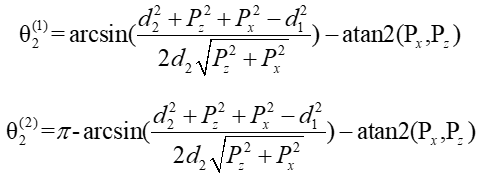
③求解
这一角度其实是最容易求解的,在利用xy平面中和
的关系就可以得到:
3. Matlab运动学解析
用matlab工具进行计算,正运动学如下:
clc;
clear;
syms d1 d2 x1 x2 theata1 theata2 theata2 px py pz;
d1=135;d2=147; %大臂小臂长度
%%正解过程
%转角输入
theata1=(110/180)*pi;theata2=(-20/180)*pi;theata3=(30/180)*pi;
px=d1*cos(theata1)+d2*cos(theata2)
py=d1*cos(theata1)*tan(theata3)+d2*cos(theata2)*tan(theata3)
pz=d1*sin(theata1)+d2*sin(theata2)就可以得到输出的位置值为:

逆运动学计算如下:
%%逆解过程
px=91.9621;py=53.0943;pz=76.5815;
%theata1
theata1_1=asin((-(d2)^2+(d1)^2+(px)^2+(pz)^2)/2/d1/sqrt((px)^2+(pz)^2))-atan2(px,pz);
theata1_2=pi-asin((-(d2)^2+(d1)^2+(px)^2+(pz)^2)/2/d1/sqrt((px)^2+(pz)^2))-atan2(px,pz);
%theata2
theata2_1=asin(((d2)^2-(d1)^2+(px)^2+(pz)^2)/2/d2/sqrt((px)^2+(pz)^2))-atan2(px,pz);
theata2_2=pi-asin(((d2)^2-(d1)^2+(px)^2+(pz)^2)/2/d2/sqrt((px)^2+(pz)^2))-atan2(px,pz);
theata3 = atan(py / px);
%角度制
theata11=theata1_1*180/pi
theata12=theata1_2*180/pi
theata21=theata2_1*180/pi
theata22=theata2_2*180/pi
theata33=theata3*180/pipx、py、pz代入正运动学求解的那个坐标(91.9621,53.0943,76.5815),运行程序可以得到以下结果:
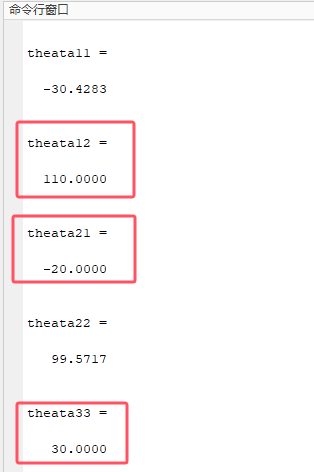
可以看到逆解得到了关节的对应转角,与我们正运动学输入的保持一致,至此分析完成~
总结
本文以双平行四边形机构的码垛机器人为对象,通过结构原理分析其运动方式,化繁为简来简化研究对象。整体上用几何法对其进行数学建模、正运动学与逆运动学分析,利用Matlab工具进行解算,验证了分析的正确性。
声明:本文以学习为目的,模型是开源机械臂。如有不足之处还请批评指正,引用本文请标明出处,谢谢您~





















&spm=1001.2101.3001.5002&articleId=153272849&d=1&t=3&u=cfde4626c1b647fc9a9cdd51ab7c798b)
 1555
1555

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








