【C++---9】红黑树的创建以及左右单旋

不管是AVL树还是红黑树都要旋转，这个旋转的代码真的烦

---

---

红黑树的创建：

• 创建一个树的颜色的枚举
• 写一个节点类，节点颜色默认红色
• 节点包含左指针域，右指针域，双亲指针域，值，颜色
• 黑红树的类中添加头结点，双亲为root，pleft指向最左侧节点，pright指向最右侧节点

#include<iostream>

using namespace std;

enum Color
{
	RED,
	BLACK
};

template<typename T>

class RBTreeNode
{
public:
	RBTreeNode(const T& data = T(), Color color = RED) : _pLeft(nullptr), _pRight(nullptr),
		_pParent(nullptr), _data(data),
		_color(color)
	{

	}

public:
	RBTreeNode<T>* _pParent;
	RBTreeNode<T>* _pLeft;
	RBTreeNode<T>* _pRight;
	T _data;
	Color _color;
};

template<typename T>

class RBTree
{
	typedef RBTreeNode<T> pNode;

public:
	RBTree()
	{
		_pHead = new pNode;
		_pHead->_pParent = nullptr;
		_pHead->_pLeft = _pHead;
		_pHead->_pRight = _pHead;
	}

---

红黑树的插入：

• 插入和二叉搜索树一样
• 关键在于违反红黑树性质之后的调整

	bool Insert(const T& data)
	{
		pNode*& pRoot = GetRoot();

		//空树插入
		if (pRoot == nullptr)
		{
			pRoot = new pNode(data, BLACK);

			pRoot->_pParent = _pHead;
			_pHead->_pLeft = pRoot;
			_pHead->_pRight = pRoot;
			return true;
		}
		else
		{
			//非空树插入,按照二叉搜索树方式
			pNode* pCur = pRoot;
			pNode* pPre = nullptr;

			while (pCur != nullptr)
			{
				pPre = pCur;

				if (pCur->_data < data)
				{
					pCur = pCur->_pRight;
				}
				else if (pCur->_data > data)
				{
					pCur = pCur->_pLeft;
				}
				else
				{
					//约定不插入相同元素
					return false;
				}
			}

			pCur = new pNode(data);

			if (pPre->_data > data)
			{
				pPre->_pLeft = pCur;
			}
			else
			{
				pPre->_pRight = pCur;
			}

			pCur->_pParent = pPre;

---

红黑树的调整：

			//检测是否破坏了二叉树的性质
			while (pPre != _pHead && pPre->_color == RED)
			{
				pNode* Grand = pPre->_pParent;

				//双亲是祖父节点的左孩子
				if (pPre == Grand->_pLeft)
				{
					pNode* uncle = Grand->_pRight;

					//情况一：叔叔节点存在,且为红
					if (uncle != nullptr && uncle->_color == RED)
					{
						//将p,u改为黑,g改为红,把g当成cur,继续向上调整
						uncle->_color = BLACK;
						pPre->_color = BLACK;
						Grand->_color = RED;

						pCur = Grand;
						pPre = pCur->_pParent;
					}

					//叔叔节点存在且为黑  ||  叔叔节点不存在
					else
					{
						//情况三：cur是双亲的右孩子,转换为情况二
						if (pCur == pPre->_pRight)
						{
							RotateL(pPre);
							swap(pPre, pCur);
						}

						//情况二：pre变黑，g变红,cur是pre的左孩子，右单旋
						pPre->_color = BLACK;
						Grand->_color = RED;
						RotateR(Grand);
					}
				}
				//双亲是祖父节点的右孩子
				else
				{
					pNode* uncle = Grand->_pLeft;

					//情况一：叔叔节点存在,且为红
					if (uncle != nullptr && uncle->_color == RED)
					{
						uncle->_color = BLACK;
						pPre->_color = BLACK;
						Grand->_color = RED;

						pCur = Grand;
						pPre = pCur->_pParent;
					}
					else
					{
						//情况三：cur是双亲的左孩子,转换为情况二
						if (pCur == pPre->_pLeft)
						{
							RotateR(pPre);
							swap(pPre, pCur);
						}
						
						pPre->_color = BLACK;
						Grand->_color = RED;
						RotateL(Grand);
					}
				}
			}
		}

		pRoot->_color = BLACK;
		_pHead->_pLeft = GetLeftMost();
		_pHead->_pRight = GetRightMost();

		return true;
	}

左单旋：

• 对某个节点左单旋，就是把其子节点拔高
• 将这个节点从左往右滑动
  

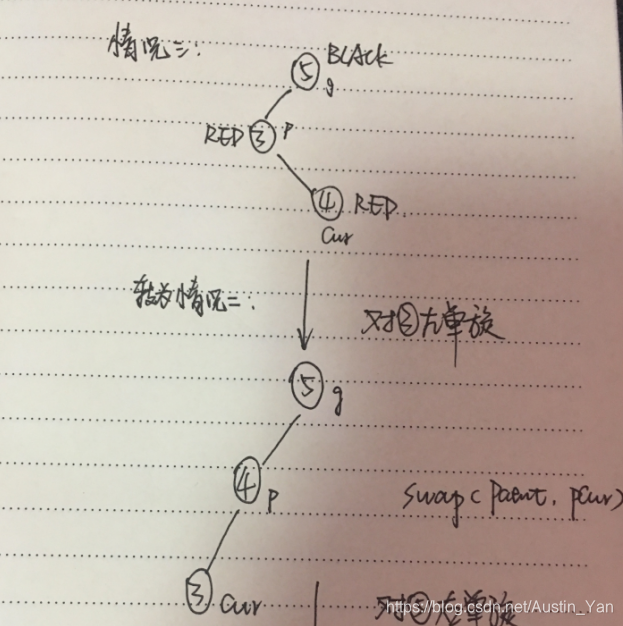
右单旋：

• 对某个节点右单旋，就是把其子节点拔高
• 将这个节点从从右往左滑动
  

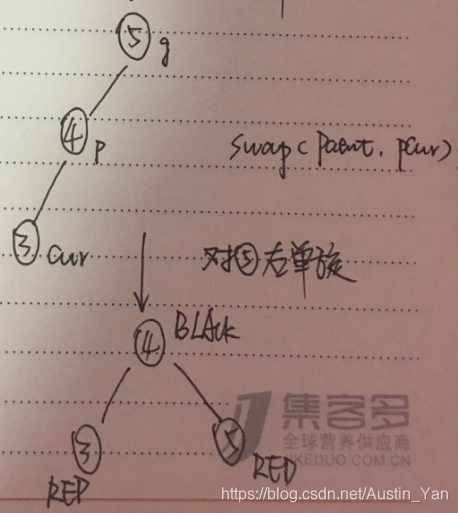
	void RotateL(pNode* parent)
	{
		pNode* subR = parent->_pRight;
		pNode* subRL = subR->_pLeft;

		parent->_pRight = subRL;

		if (subRL != nullptr)
		{
			subRL->_pParent = parent;
		}

		subR->_pLeft = parent;

		pNode* pParent = parent->_pParent;

		parent->_pParent = subR;
		subR->_pParent = pParent;

		if (pParent == _pHead)
		{
			_pHead->_pParent = subR;
		}
		else
		{
			if (pParent->_pLeft == parent)
			{
				pParent->_pLeft = subR;
			}
			else
			{
				pParent->_pRight = subR;
			}
		}
	}

	void RotateR(pNode* parent)
	{
		pNode* subL = parent->_pLeft;
		pNode* subLR = subL->_pRight;

		parent->_pLeft = subLR;

		if (subLR != nullptr)
		{
			subLR->_pParent = parent;
		}

		subL->_pRight = parent;

		pNode* pParent = parent->_pParent;

		subL->_pParent = pParent;
		parent->_pParent = subL;

		if (pParent == _pHead)
		{
			_pHead->_pParent = subL;
		}
		else
		{
			if (pParent->_pLeft == parent)
			{
				pParent->_pLeft = subL;
			}
			else
			{
				pParent->_pRight = subL;
			}
		}
	}

---