论文笔记：Non-Local Neural Network

论文笔记：Non-Local Neural Network

Abstract

卷积和循环操作都一次只在一个局部neighborhood上操作。

受到传统计算机视觉中非局部中值计算的启发，作者决定使用此方法在深度学习上。

公式

通用公式：
$${\mathbf{y}}_i=\frac{1}{\mathcal{C}(\mathbf{x})}\sum _{\forall j}f\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)g\left({\mathbf{x}}_j\right)$$
$\mathbf{y}$ is output. $x$ 是输入信号。$i$是输出的值第i位置的值，j代表所有可能位置。

$\mathbf{y}$ 与$\mathbf{x}$ 具有相同大小的维度。

$C(x)$是正则化常量

$f$代表两处变量的关系

非局部模块十分的灵活，可以放在网络的前面，可以很容易与循环层，卷积层放到一起。

实例

为了简便考虑，g就作为一个简单的线性变换$g\left({\mathbf{x}}_j\right)=W_g{\mathbf{x}}_j$， 其中$W_g$是作为需要学习的参数。

接下来我们考虑函数$f$:

Gaussian

$$f\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=e^{{\mathbf{x}}_i^T{\mathbf{x}}_j}$$

自然的想法就是使用高斯函数。其中$\mathcal{C}(\mathbf{x})={\sum }_{\forall j}f\left({\mathbf{x}}_i,{\mathbf{x}}_j\right).$

Embedded Gaussian

$$f\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=e^{\theta {\left({\mathbf{x}}_i\right)}^T\varphi \left({\mathbf{x}}_j\right)}$$

其中$\theta \left({\mathbf{x}}_i\right)=W_{\theta }{\mathbf{x}}_i$ and $\varphi \left({\mathbf{x}}_j\right)=W_{\varphi }{\mathbf{x}}_j$， 我们同样可以设置$\mathcal{C}(\mathbf{x})={\sum }_{\forall j}f\left({\mathbf{x}}_i,{\mathbf{x}}_j\right).$

于是这个计算就变成了softmax： $\mathbf{y}=\mathrm{softmax}\left({\mathbf{x}}^T{W}_{\theta }^T{W}_{\varphi }\mathbf{x}\right)g(\mathbf{x})$

Dot Product

$$f\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\theta {\left({\mathbf{x}}_i\right)}^T\varphi \left({\mathbf{x}}_j\right)$$

设置$C(x)=N$, 其中N是位置$x$的个数

Concatenation

$$f\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\mathrm{ReLU}\left({\mathbf{w}}_f^T\left[\theta \left({\mathbf{x}}_i\right),\varphi \left({\mathbf{x}}_j\right)\right]\right)$$

其中$W_f$是一个将组合映射到标量的权重向量。 我们设置 $C（x）=N$.

非局部块

定义：
$${\mathbf{z}}_i=W_z{\mathbf{y}}_i+{\mathbf{x}}_i$$
$y_i$是式子（1）的结果， $+x_i$表示残差连接（residual connection）是为了使我们可以添加非局部块到任何提前训练（pre-trained）的模型而不破坏模型结构（比如如果$W_z$被初始化为0）。图二是一个例子

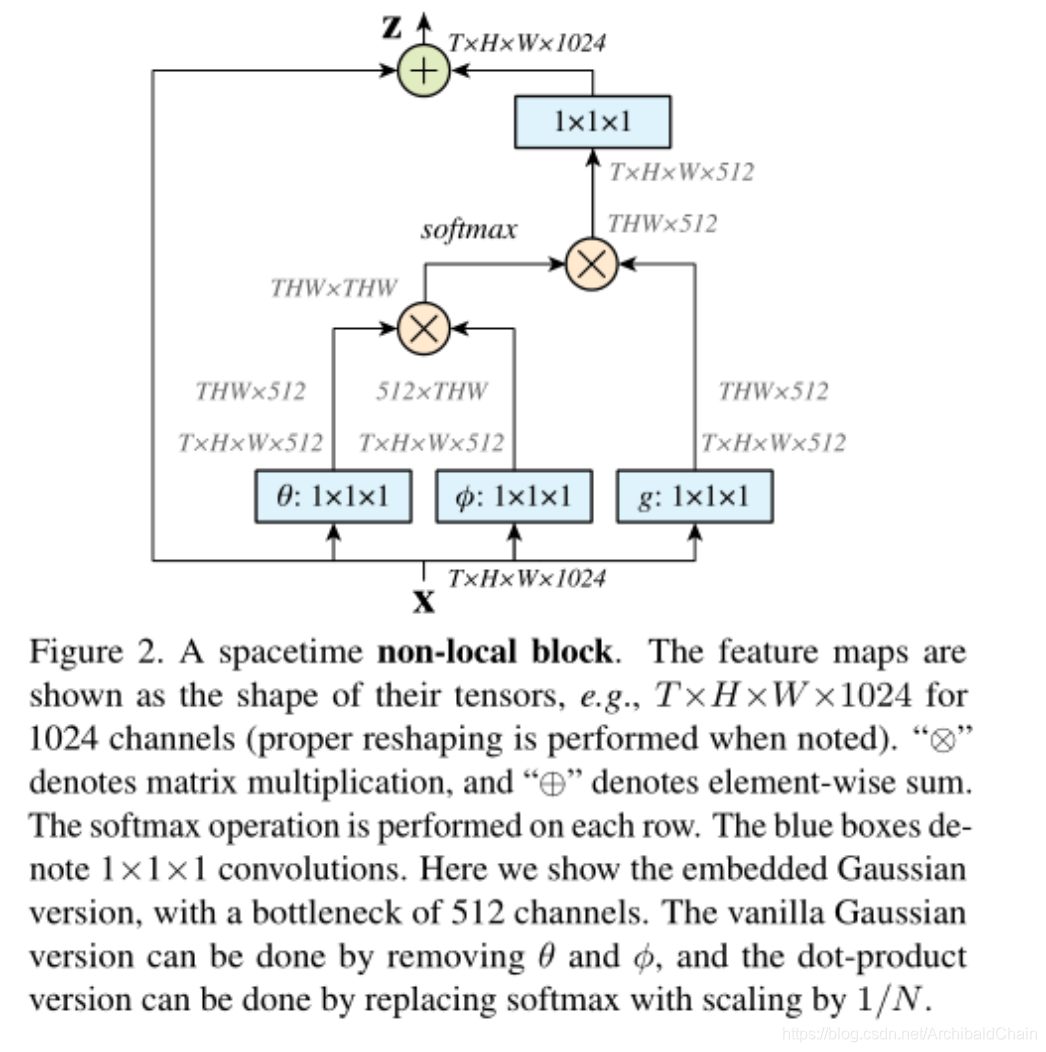
这里可以通过矩阵乘法和加法巧妙的实现非局部变换。

写下来截图的部分便是前文提到的embedding Gaussian的$f$

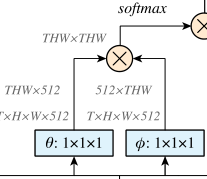
这里$\theta$和$\varphi$函数都对输入信号进行了降低通道处理。（从$T\times W\times H\times 1024$ 降到 $T\times W\times H\times 512$）这样可以降低计算，同时也符合瓶颈算法设计。

同时文中说可以将（1）式修改为
$$\frac{1}{c(\hat{\mathbf{x}})}\sum _{\forall j}f\left({\mathbf{x}}_i,{\hat{\mathbf{x}}}_j\right)g\left({\hat{\mathbf{x}}}_j\right)$$
其中$\hat{x}$表示池化后$x$的子采样。 我们通过给$\theta$和$\varphi$添加赤化层达到这个效果，从而可以使得计算降低1/4.

实现细节

2D ConvNet baseline (C2D)

输入的是32帧的224x224像素视频。整个模型直接使用 ResNet 在ImageNet pre-trained 的权重。只有在赤化层使用了时域。

Inflated 3D ConvNet (I3D)

把卷积核在时域上膨胀开。比如2D上的$k\times k$ 膨胀成 $t\times k\times k$

因为3D计算量过于旁大，所以每两个瓶颈只膨胀一个卷积核。要么膨胀3x3成3x3x3；要么膨胀1x1成3x1x1

Non-local Network

作者在两种baseline上分别添加了1，5，10个非局部块做实验

大，所以每两个瓶颈只膨胀一个卷积核。要么膨胀3x3成3x3x3；要么膨胀1x1成3x1x1

Non-local Network

作者在两种baseline上分别添加了1，5，10个非局部块做实验

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-crjZNYL2-1596448249812)(image-20200803174903515.png)]