统计RGB格式和YUV格式的图像文件中各分量概率分布，并计算它们的熵

实验目的：两图像文件的分辨率为256*256，其中YUV的采样格式为4：2：0，编写代码，画出两文件中各分量的概率分布图像、计算各分量的熵并加以说明

一 存储格式

1 RGB文件的存储格式

按像素位置从左至右、从上至下依次存储，其中每个像素的分量都按B、G、R顺序排列（BGRBGRBGR…）

2 YUV文件的存储格式

本次实验中，yuv文件的采样格式为4：2：0

其存储格式为YV12，YU12(4:2:0)，即按从左至右、从上至下的顺序，先存储所有像素的Y分量，再存储所有像素的U(Cb)分量，再存储所有像素的V(Cr)分量

二 RGB文件处理

1 计算R、G、B分量的各强度值的出现频次

import numpy as np
import math
import matplotlib.pyplot as plt

file = open("D:\\Users\\AzureShield\\Desktop\\down.rgb","rb") 
##获取文件路径。需要注意的是，默认r读取时，Python会将字节\x1a(26)转换成的字符视作文档结束符（EOF），
##故若不用二进制rb读取，可能产生文档读取不全的现象

data = file.read() 
##读取图像文件，并按从左至右、从上至下的顺序，将每个像素的B、G、R大小信息按次序存储在data数组中，占用空间：256*256*3Byte

file.close

data = [int (x) for x in data]  ##将数据转换为整型，便于后续计算
data_B = []
data_G = []
data_R = []

for i in range(1,256*256*3):
    if(divmod(i-1,3)[1]==0):
        data_B.append(data[i-1])
    if(divmod(i-1,3)[1]==1):
        data_G.append(data[i-1])
    if(divmod(i-1,3)[1]==2):
        data_R.append(data[i-1])
##divmod(x,y)函数返回一个包含商和余数的元组，分别存放在[0]和[1]中

count_B = np.zeros(255) 
##zeros(a)函数：生成一个a*a的零矩阵,此处当作一般数组使用。RGB分量取值范围是0~255，从count[0]到count[255]，为分量的每个强度值单独计数
count_G = np.zeros(255)
count_R = np.zeros(255)
for i in data_B:
    count_B[i-1] = count_B[i-1]+1
for i in data_G:
    count_G[i-1] = count_G[i-1]+1
for i in data_R:
    count_R[i-1] = count_R[i-1]+1
for i in range(1,256):
    count_B[i-1] = count_B[i-1] / 65536
for i in range(1,256):
    count_G[i-1] = count_G[i-1] / 65536
for i in range(1,256):
    count_R[i-1] = count_R[i-1] / 65536

plt.plot(count_B,'b')
plt.plot(count_G,'g')
plt.plot(count_R,'r')
plt.legend(['B','G','R'])
plt.show()

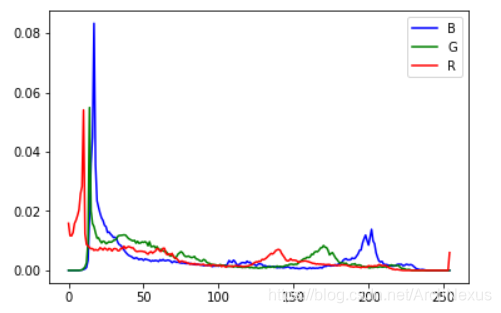
2 计算R、G、B各分量的熵

##对B、G、R进行求熵
H_B=0
H_G=0
H_R=0
for i in range(1,256):
    if(count_B[i-1]==0):
        H_B = H_B - 0
    else:
        H_B = H_B - count_B[i - 1] * math.log2(count_B[i-1])
    if (count_G[i-1] == 0):
        H_G = H_G - 0
    else:
        H_G = H_G - count_G[i - 1] * math.log2(count_G[i-1])
    if (count_R[i-1] == 0):
        H_R = H_R - 0
    else:
        H_R = H_R - count_R[i - 1] * math.log2(count_R[i-1])
print(H_B,H_G,H_R)

R	G	B
7.229	7.178	6.857

三 YUV文件处理

除去存储格式与RGB有所不同，其他代码部分与前文基本一致

import numpy as np
import math
import matplotlib.pyplot as plt

f = open("D:\\Users\\AzureShield\\Desktop\\down.yuv","rb")
data = f.read()
f.close()
data = [int(x) for x in data]
##此处YUV图像文件的存储格式是先存储所有Y，再存储所有U(Cb)，再存储所有V(Cr)，
##即Y分量偏移范围[0,256*256-1]，U分量偏移范围[256*256,256*256+256*256/4]，V分量偏移范围[81919,98303]，文件大小一共98304字节
##其他部分的代码与RGB格式基本一致
data_Y=[]
data_U=[]
data_V=[]
for i in range(1,256*256):
    data_Y.append(data[i-1])
for i in range(256*256+1,81920):
    data_U.append(data[i-1])
for i in range(81920+1,98304):
    data_V.append(data[i-1])
count_Y=np.zeros(255)
count_U=np.zeros(255)
count_V=np.zeros(255)
for i in data_Y:
    count_Y[i-1]=count_Y[i-1]+1
for i in data_U:
    count_U[i-1]=count_U[i-1]+1
for i in data_V:
    count_V[i-1]=count_V[i-1]+1
for i in range(1,256):
    count_Y[i-1] = count_Y[i-1] / 65536
    count_U[i-1] = count_U[i-1] / 16384
    count_V[i-1] = count_V[i-1] / 16384
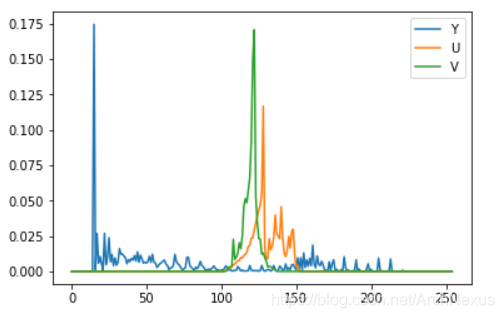
plt.plot(count_Y)
plt.plot(count_U)
plt.plot(count_V)
plt.legend(['Y','U','V'])
plt.show()

##计算Y、U、V分量的熵
H_Y=0
H_U=0
H_V=0
for i in range(1,256):
    if(count_Y[i-1]==0):
        H_Y = H_Y - 0
    else:
        H_Y = H_Y - count_Y[i-1] * math.log2(count_Y[i-1])
    if (count_U[i-1] == 0):
        H_U = H_U - 0
    else:
        H_U = H_U - count_U[i-1] * math.log2(count_U[i-1])
    if (count_V[i-1] == 0):
        H_V = H_V - 0
    else:
        H_V = H_V - count_V[i-1] * math.log2(count_V[i-1])
print(H_Y,H_U,H_V)

Y	U	V
6.332	5.126	4.113

四 结论

可以看到，两幅相同内容的图片，YUV分量的熵明显低于RGB分量，理论上可认为RGB格式的去相关性更好，同等存储容量下携带的信息量更大。
但实际应用中，一般是YUV更优，这是因为人眼对色度信号的感知力弱于亮度信号，故压缩流程中，一般要将RGB信号先转化为YUV信号，这样就可以较大幅压缩U、V分量，减小数据量。
笔者考虑到，如果down.yuv是已经经过压缩的图片，那么可能产生数据损失，自然熵较小、冗余度较高。

五 鸣谢

1 hzd_01

python的写法部分相当出色！有一些小的谬误，但整体上简洁漂亮，避免了通过C++进行传统频次计算的繁琐感。

https://blog.youkuaiyun.com/weixin_43878172/article/details/114499192?utm_medium=distribute.pc_relevant.none-task-blog-baidujs_title-0&spm=1001.2101.3001.4242

2《使用C++处理YUV文件》

提供了YUV格式采样结构和存储结构的阐释。

https://blog.youkuaiyun.com/Cross_Entropy/article/details/104510615?spm=1001.2014.3001.5501