【LeetCode Top 100】48. Rotate Image【Medium】【JAVA】

这篇博客主要解析了LeetCode中的48题——旋转图像，通过分析奇数和偶数矩阵的情况，探讨了旋转90度时各点坐标的变化规律，并给出了具体的JAVA实现代码，最终展示了运行结果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 题目

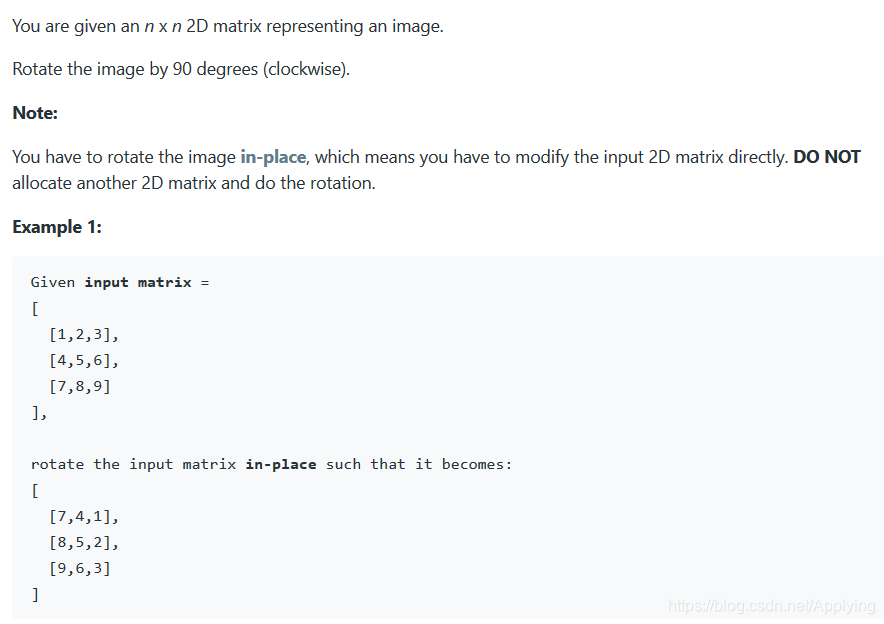
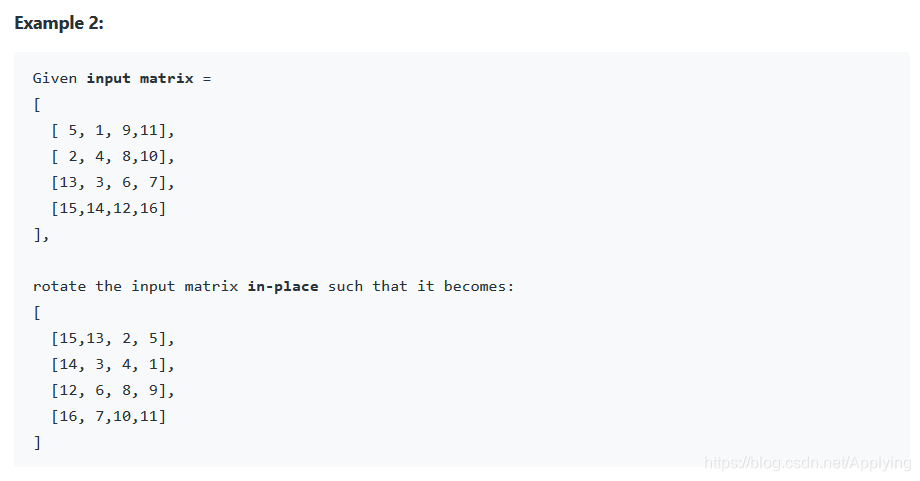
在这里插入图片描述

2. 题意

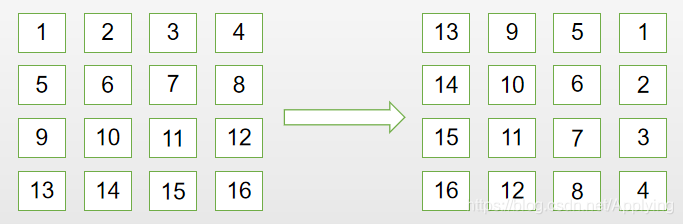
题目很好理解，即将一个矩阵旋转90度，这里要注意是顺时针旋转，不能搞混旋转的方向。

3. 思路

旋转90度，我们可以先观察每一个点的旋转情况：
先取 n 为奇数，n = 3 的情况分析：
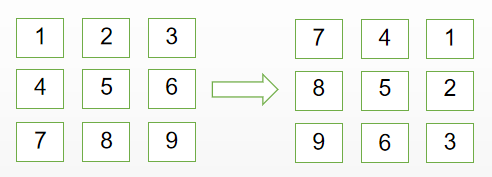
在这里插入图片描述
观察上面的图，可以发现，中间部分不会旋转，4个小矩形，绕着中心进行旋时针旋转。如下图：

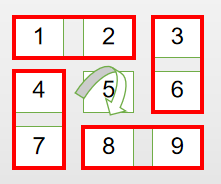
再取 n 为偶数，n = 4 的情况分析：

在这里插入图片描述
可以看出，即从正方形最中心的地方，将四个小正方形，进行旋转。

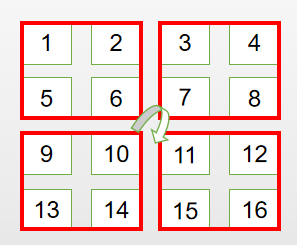
在这里插入图片描述
因此，该思路对于 n 为奇数或偶数都适用，现在考虑旋转过程中各个点的坐标的变化情况：
考虑四个小矩形中任一个点的旋转规律：如下图，正方形长度为 n，点 a，b，c，d刚好对应四个小矩形旋转过程中相同位置的点，我们来考虑四个点之间的坐标关系：
在这里插入图片描述
假设点 a 坐标为(i, j)，即第 i 行，第 j 列。先考虑行的关系，对于点 a，其位于第 i 行，即其在小矩形中，距离上方的边，距离为 i，可以进行画图：

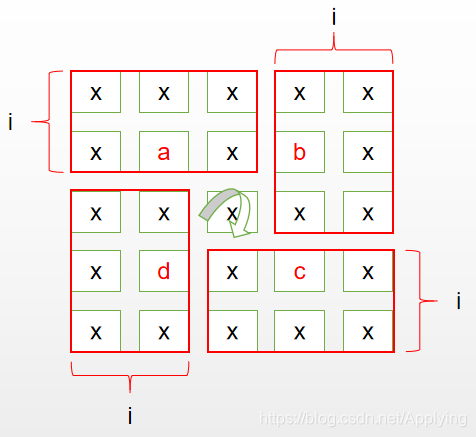
通过图上的情况，我们可以整理四个点的坐标：

	行	列
a	i	j
b	未知	n - i
c	n - i	未知
d	未知	i

再考虑列的关系，对于点 a，其位于第 j 行，即其在小矩形中，距离左侧的边，距离为 j，可以进行画图：
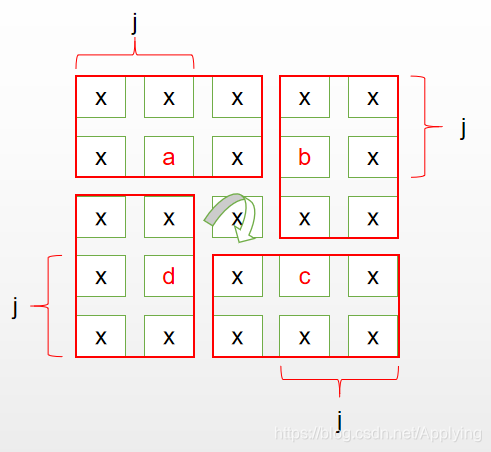
在这里插入图片描述
通过图上的情况，我们可以整理四个点的坐标：

	行	列
a	i	j
b	j	n - i
c	n - i	n - j
d	n - j	i

有了旋转的范围（四个小矩形），旋转点之间的关系，即可以进行旋转了，代码如下。

4. 代码

	public void rotate(int[][] matrix) {
        for (int i = 0; i < matrix.length / 2; i++) {
            for (int j = 0; j < (matrix.length + 1) / 2; j++) {
                int temp = matrix[matrix.length - j - 1][i];
                matrix[matrix.length - j - 1][i] = matrix[matrix.length - i - 1][matrix.length - j - 1];
                matrix[matrix.length - i - 1][matrix.length - j - 1] = matrix[j][matrix.length - i - 1];
                matrix[j][matrix.length - i - 1] = matrix[i][j];
                matrix[i][j] = temp;
            }
        }
    }